还剩37页未读，
继续阅读
2023年高考数学人教A版（2019）大一轮复习--3.2 函数的单调性与最值（课件）
展开这是一份2023年高考数学人教A版（2019）大一轮复习--3.2 函数的单调性与最值（课件），共45页。PPT课件主要包含了内容索引，强基础增分策略，增素能精准突破，单调递增，单调递减，单调区间，函数的最值，fx≤M，fx0M，fx≥M等内容，欢迎下载使用。
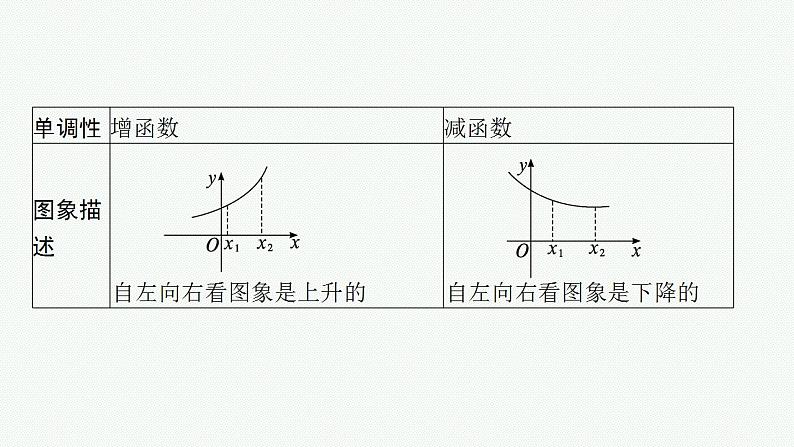
知识梳理1.函数的单调性(1)单调函数的定义
f(x1)
微点拨函数单调性定义的等价形式
(2)单调性、单调区间的定义若函数y=f(x)在区间D上 或 ,则称函数y=f(x)在这一区间上具有(严格的)单调性,区间D叫做y=f(x)的 .
微思考如何判断复合函数的单调性?
提示 若构成复合函数的内、外层函数单调性相同,则复合函数为增函数,否则为减函数,简称“同增异减”.
常用结论1.若f(x),g(x)均是区间A上的增(减)函数,则f(x)+g(x)也是区间A上的增(减)函数;若f(x),g(x)分别是区间A上的增函数和减函数,则f(x)-g(x)是区间A上的增函数.2.若k>0,则kf(x)与f(x)单调性相同;若k<0,则kf(x)与f(x)单调性相反.3.闭区间上的图象连续的函数一定存在最大值和最小值,当函数在闭区间上单调时,最值一定在端点处取到.
对点演练1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)如果f(-1)
解析 y=-2x在(0,+∞)上单调递减,故A错误;y=(x-1)2在(0,+∞)上先减后增,故B错误;y= 在(0,+∞)上单调递减,故C错误;y=|x+2|在(0,+∞)上单调递增,符合题意.
解析 由单调性的定义可知f(x)在[2,+∞)上单调递增,因此f(x)在[2,b]上的最大值与最小值分别为f(b),f(2),所以有 ,解得b=3.
考向1.证明或判断函数的单调性典例突破例1.(1)(2021山东青岛高三月考)下列函数在区间(0,+∞)上单调递减的是( )A.f(x)=ln x B.f(x)=e-x
(2)判断并证明函数f(x)= 在(-1,+∞)上的单调性.
(2) 解 函数f(x)在(-1,+∞)上单调递增.
方法总结利用定义法证明或判断函数的单调性的步骤
对点训练1(2021宁夏银川高三二模)设函数f(x)=x2- ,则f(x)( )A.是偶函数,且在(-∞,0)上单调递增B.是偶函数,且在(-∞,0)上单调递减C.是奇函数,且在(-∞,0)上单调递增D.是奇函数,且在(-∞,0)上单调递减
考向2.求函数的单调区间典例突破例2.求下列函数的单调区间:(1)f(x)=x2+4x-1;(2)f(x)=|x+1|+|x-2|;(3)f(x)=lg3(4x-x2).
解 (1)函数f(x)的定义域为R,其图象是开口向上的抛物线,抛物线的对称轴是直线x=-2,所以函数的单调递增区间是[-2,+∞),单调递减区间是(-∞,-2].
(2)函数f(x)的定义域为R,且f(x)=|x+1|+|x-2|= 该函数的大致图象如图:由图象可知,该函数的单调递增区间是[2,+∞),单调递减区间是(-∞,-1].
(3)由4x-x2>0,解得0
对点训练2(1)(2021山东聊城高三月考)已知函数f(x)的图象如图所示,则函数 的单调递增区间为( )A.(-∞,-3]和[0,3]B.[-3,0]和[3,+∞)C.(-∞,-5)和[0,1)D.(-1,0]和(5,+∞)
(2)(2021浙江杭州高三月考)函数y= 的单调递增区间为 .
答案 (1)C (2)(-∞,-1]
解析 (1)因为y= 在(0,+∞)上为减函数,所以只要求y=f(x)的单调递减区间,且f(x)>0.由图可知,使得y=f(x)单调递减且满足f(x)>0的x的取值范围是(-∞,-5)∪[0,1),因此g(x)= 的单调递增区间为(-∞,-5)和[0,1),故选C.
典例突破例3.求下列函数的最值:
方法总结求函数最值的常见方法(1)单调性法:若f(x)在[a,b]上单调递增(减),则f(a),f(b)分别是f(x)在区间[a,b]上取得的最小(大)值、最大(小)值.(2)图象法:对于由基本初等函数变化而来的函数,通过观察函数图象的最高点或最低点确定函数的最值.(3)换元法:形如y=ax+b± 型的函数,可用此法求其最值.(4)基本不等式法:注意应用基本不等式的条件“一正、二定、三相等”.(5)导数法:利用导数研究复杂函数的极值和最值,然后求出值域.
对点训练3(1)(2021江苏南通高三模拟)函数y= ,x∈(m,n]的最小值为0,则m的取值范围是( )A.(1,2)B.(-1,2)C.[1,2)D.[-1,2)
(2)函数f(x)=min{-x+3,lg2x},其中min{a,b}= 的最大值为 .
答案 (1)D (2)1
解析 (1)函数y= -1,可以判断函数在区间(-1,+∞)上单调递减,且f(2)=0,所以n=2.根据题意,当x∈(m,n]时,ymin=0,故m的取值范围是[-1,2).(2)由函数的图象(图略)可知,函数在x=2处取得最大值1.
考向1.利用单调性比较大小典例突破
例4.(2021江苏无锡高三期中)已知函数f(x)=lg x- x,f(m)=1,且0
解析 由于y=lg x是定义域上的增函数,y= x是定义域上的减函数,因此f(x)=lg x- x在(0,+∞)上单调递增.又0
对点训练4(2021四川遂宁高三三模)已知函数f(x)=2-x-4x,若a=0.3-0.25,b=lg0.250.3,c=lg0.32.5,则( )A.f(b)
答案 (3,4) 解析 因为f(x+1)是奇函数,所以f(x)的图象关于(1,0)对称,因此f(1-x)+f(1+x)=0.又因为f(x)在[1,+∞)上单调递减,所以f(x1)+f(x2)>0等价于x1+x2<2,因此不等式f(lg2(x-3))+f(lg2x)>0等价于lg2(x-3)+lg2x<2,即lg2[x(x-3)]
对点训练5(2021北京西城高三月考)已知函数f(x)= 若f(2-x2)>f(x),则实数x的取值范围是 .
答案 (-2,1)
解析 由f(x)的图象可知f(x)是定义在R上的增函数,而f(2-x2)>f(x),则2-x2>x,解得-2
答案 (1)D (2)C
突破技巧根据单调性求参数的值或取值范围(1)如果函数解析式已知,欲求参数在区间中,可先求出函数的单调区间,然后由所给区间是相应单调区间的非空子集构建不等式(组)求解参数范围.(2)如果已知分段函数的单调性求参数的取值范围,除了要求每一段均满足相应的单调性外,还必须要求分段点处的函数值满足相应的大小关系.
对点训练6(1)(2021浙江绍兴高三月考)若函数f(x)=-x2+4ax在[1,3]内不单调,则实数a的取值范围是 .
(2)(2021江西南昌高三期中)函数f(x)= 是单调函数,则实数a的取值范围是 .
相关课件
高中数学高考通用版2020版高考数学大一轮复习第5讲函数的单调性与最值课件文新人教A版：
这是一份高中数学高考通用版2020版高考数学大一轮复习第5讲函数的单调性与最值课件文新人教A版，共45页。PPT课件主要包含了单调函数的定义，上升的，下降的，知识聚焦，增函数或减函数，区间D，fx0M，fx≥M，题组一常识题，题组二常错题等内容，欢迎下载使用。
通用版高考数学(文数)一轮复习第5讲《函数的单调性与最值》课件 (含答案)：
这是一份通用版高考数学(文数)一轮复习第5讲《函数的单调性与最值》课件 (含答案)，共44页。PPT课件主要包含了单调函数的定义，上升的，下降的，知识聚焦，增函数或减函数，区间D，fx0M，fx≥M，题组一常识题，题组二常错题等内容，欢迎下载使用。
2023年高考数学人教A版（2019）大一轮复习--4.2 利用导数研究函数的单调性（课件）：
这是一份2023年高考数学人教A版（2019）大一轮复习--4.2 利用导数研究函数的单调性（课件），共38页。PPT课件主要包含了内容索引，强基础增分策略，增素能精准突破，单调递增，单调递减，易错警示，答案D等内容，欢迎下载使用。
