2020-2021学年7.4 三角函数应用多媒体教学ppt课件

这是一份2020-2021学年7.4 三角函数应用多媒体教学ppt课件，文件包含74三角函数应用pptx、74三角函数应用doc等2份课件配套教学资源，其中PPT共55页， 欢迎下载使用。

第7章 三角函数
7.4　三角函数应用
课标要求
1.会用三角函数解决简单的实际问题.2.体会可以利用三角函数构建刻画事物周期变化的数学模型.
素养要求
通过实际问题，构建三角函数数学模型，重点提升学生的数学抽象、数学运算和数学建模素养.
问题导学预习教材必备知识探究
互动合作研析题型关键能力提升
拓展延伸分层精练核心素养达成
内容索引
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1
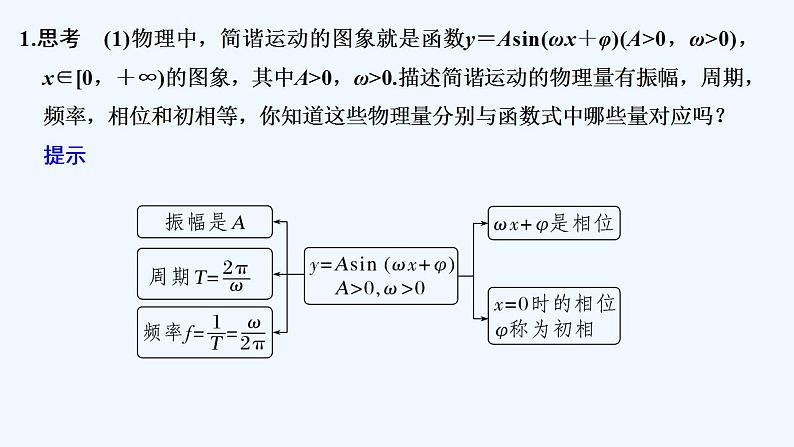
1.思考　(1)物理中，简谐运动的图象就是函数y＝Asin(ωx＋φ)(A>0，ω>0)，x∈[0，＋∞)的图象，其中A>0，ω>0.描述简谐运动的物理量有振幅，周期，频率，相位和初相等，你知道这些物理量分别与函数式中哪些量对应吗？ 提示　
(2)y＝Asin(ωx＋φ) 的解析式中字母值的确定：根据函数y＝Asin(ωx＋φ)(A>0，ω>0)的部分图象如何求A?提示　①根据图象的最高点(或最低点)确定A.
②根据函数y＝Asin(ωx＋φ)(A>0，ω>0)的部分图象如何确定ω？
2.填空　简谐运动(单摆、弹簧振子等)是一种周期运动，其运动规律可以用三角函数表达为y＝Asin(ωx＋φ)，其中x表示______，y表示相对于__________的偏离； ①A表示物体运动时离开平衡位置的最大距离，称为______；
时间
平衡位置
振幅
温馨提醒　解三角函数应用问题的基本步骤
3.做一做　(1)思考辨析，判断正误①函数y＝Asin(ωx＋φ)，x∈R的最大值为A.(　　)提示　当A>0时，ymax＝A；当A942，又ω∈N*，故所求最小正整数ω＝943.
题型二　三角函数模型在生活中的应用
例2 如图，游乐场中的摩天轮匀速旋转，每转一圈需要12分钟，其中心O距离地面40.5米，半径40米.如果你从最低处登上摩天轮，那么你与地面的距离将随时间的变化而变化，以你登上摩天轮的时刻开始计时.请解答下列问题.
(1)求出你与地面的距离y与时间t之间的函数解析式；
解　可以用余弦型函数来表示该函数解析式，由已知可设y＝40.5－40cos ωt(t≥0)，由周期为12分钟可知，当t＝6分钟时到达最高点，即函数取得最大值，故80.5＝40.5－40cos 6ω，
(2)当你第四次距离地面60.5米时，用了多长时间？
解得t＝4＋12k，k∈N或t＝8＋12k，k∈N，又∵t≥0，故第四次距离地面60.5米时，用了12＋8＝20(分钟).
(3)当你登上摩天轮2分钟后，你的朋友也在摩天轮最低处登上摩天轮，问：你的朋友登上摩天轮多长时间后，你和你的朋友与地面的距离之差最大？并求出最大值.
解　与地面的距离之差最大，此时你必须在你的朋友的正上方，或你的朋友在你的正上方，由周期性知，再过2分钟后，你恰好在你的朋友的正上方；再过半个周期时，恰相反，故过(6k＋2)(k∈N)分钟后，你和你的朋友与地面的距离之差最大，最大值为40米.
解决三角函数的实际应用问题必须按照一般应用题的解题步骤执行：(1)认真审题，理清问题中的已知条件与所求结论.(2)建立三角函数模型，将实际问题数学化.(3)利用三角函数的有关知识解决关于三角函数的问题，求得数学模型的解.(4)根据实际问题的意义，得出实际问题的解.(5)将所得结论返回、转译成实际问题的答案.
(2)若有一种细菌在15 ℃到25 ℃之间可以生存，那么在这段时间内，该细菌能生存多长时间？
课堂小结
1.掌握2个应用(1)三角函数在物理中的应用.(2)三角函数在生活中的应用.2.掌握4个步骤(1)收集数据，观察数据，发现是否具有周期性的重复现象.(2)制作散点图，选择函数模型进行拟合.(3)利用三角函数模型解决实际问题.(4)根据问题的实际意义，对答案的合理性进行检验.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
A.5 B.6 C.8 D.10
C
C
A
C
5.(多选)如图是某市夏季某一天的温度变化曲线，若该曲线近似地满足函数y＝Asin(ωx＋φ)＋B(A＞0，ω＞0，0