初中数学沪科版八年级下册19.3 矩形 菱形 正方形图片ppt课件

这是一份初中数学沪科版八年级下册19.3 矩形 菱形 正方形图片ppt课件，共27页。PPT课件主要包含了学习目标及重难点，课程导入，课程讲授，探索1矩形的性质，生活中的矩形，设∠A90°，∴ACBD，矩形的对边相等，ABDC，∠ABC∠DCB等内容，欢迎下载使用。
1.理解矩形的概念，知道矩形与平行四边形的区别与联系，掌握直角三角形斜边中线的性质，并会简单的运用.（重点）2.会证明矩形的性质，会用矩形的性质解决简单的问题.（重点、难点）
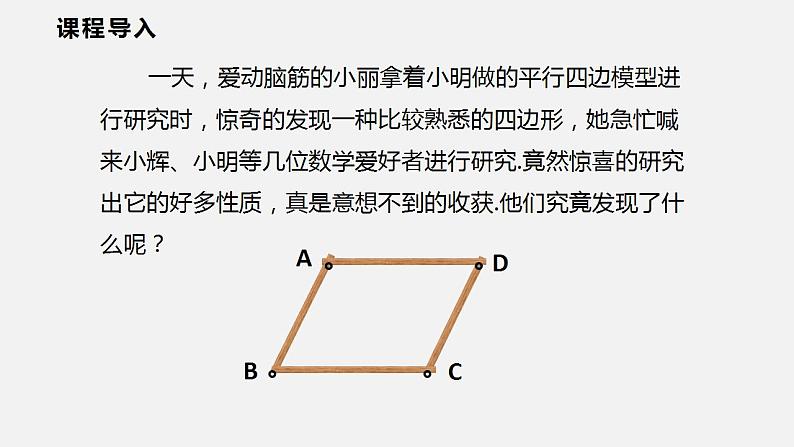
一天，爱动脑筋的小丽拿着小明做的平行四边模型进行研究时，惊奇的发现一种比较熟悉的四边形，她急忙喊来小辉、小明等几位数学爱好者进行研究.竟然惊喜的研究出它的好多性质，真是意想不到的收获.他们究竟发现了什么呢？
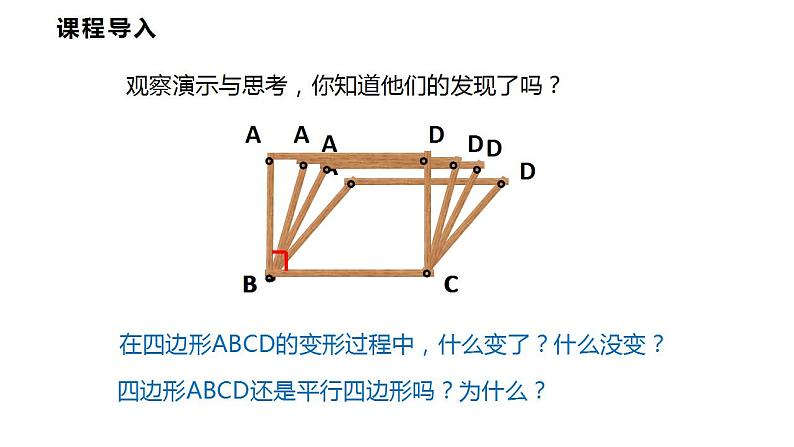
观察演示与思考，你知道他们的发现了吗？
在四边形ABCD的变形过程中，什么变了？什么没变？
四边形ABCD还是平行四边形吗？为什么？
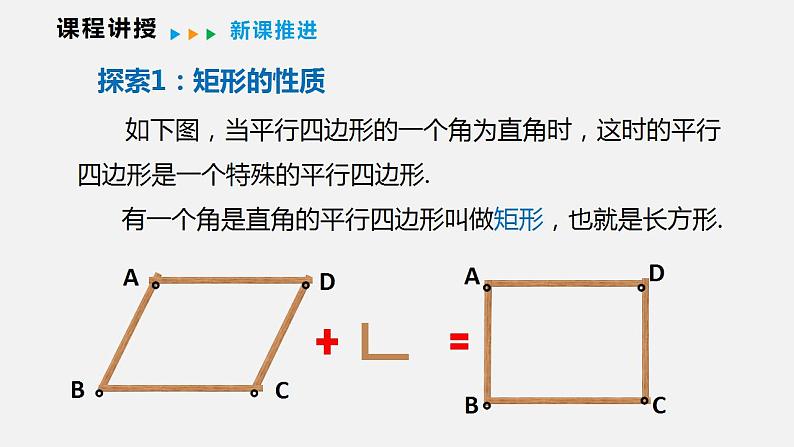
如下图，当平行四边形的一个角为直角时，这时的平行四边形是一个特殊的平行四边形. 有一个角是直角的平行四边形叫做矩形，也就是长方形.
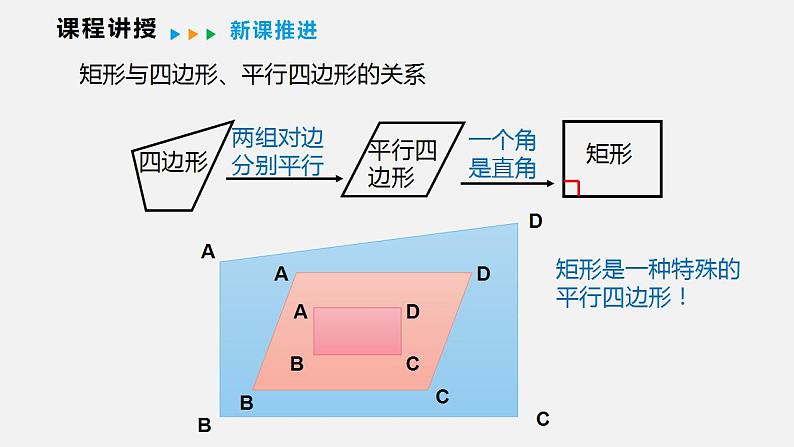
矩形与四边形、平行四边形的关系
矩形是一种特殊的平行四边形！
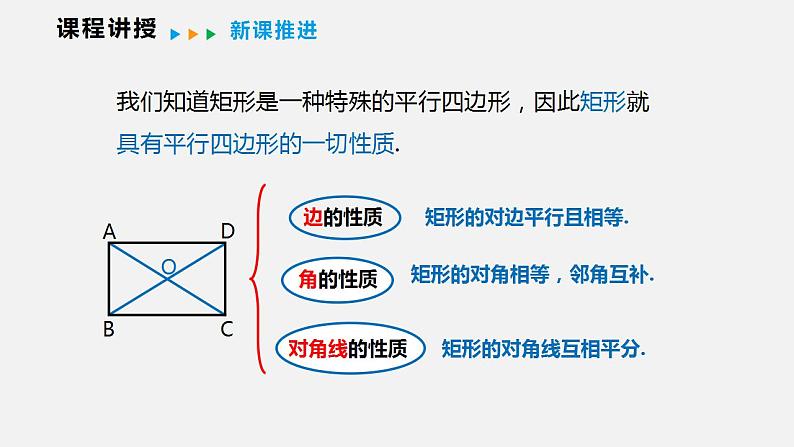
我们知道矩形是一种特殊的平行四边形，因此矩形就具有平行四边形的一切性质.
矩形的对边平行且相等.
矩形的对角相等，邻角互补.
矩形的对角线互相平分.
思考：矩形除了具有一般平行四边形的性质外，它的边、角和对角线还具有哪些特殊的性质呢？
猜想1：矩形的四个角都是直角.
猜想2：矩形的对角线相等．
证明：由定义，矩形必有一个角是直角，
∵ 在矩形ABCD中，AB∥ CD，AD∥ BC
∴ ∠B=∠C=∠D=90°
猜想 1：矩形的四个角都是直角.
∠A=∠B=∠C=∠D=90°
如图，四边形ABCD是矩形.
(两直线平行，同旁内角互补)
即 矩形ABCD的四个角都是直角.
已知：在矩形ABCD中，对角线AC和BD相交于点O.求证：AC = BD
∵ 四边形ABCD是矩形
∴ △ABC≌△DCB(SAS)
∠ABC = ∠DCB = 90°
(矩形的四个角都是直角)
在△ABC和△DCB中
从角上看：矩形的四个角都是直角．
从对角线上看：矩形的两条对角线相等．
∵ 四边形ABCD是矩形∴ ∠ABC=∠BCD=∠CDA=∠DAB=90°
∵ 四边形ABCD是矩形∴ AC=BD
(矩形的两条对角线相等)
∵ 四边形ABCD是矩形∴ AC=BD，且 OA=OB=OC=OD
矩形的对角线相等且互相平分
思考1 如图，矩形ABCD的对角线AC、BD相交于点O，图中有多少个直角三角形？有多少个等腰三角形？
探索2：直角三角形的性质
矩形的每条对角线把矩形分成两个直角三角形，矩形的两条对角线将矩形分成四个等腰三角形.
矩形问题
直角三角形和等腰三角形来解决
思考2 如果从矩形ABCD中平移出Rt△ABC及线段OB，OB与AC又有什么样的关系？
OB = AC .
∴ 四边形ABCD是平行四边形
∵ ∠ABC=90°
∴ 平行四边形ABCD是矩形
已知：如图，在Rt△ABC中，∠ABC=90°，OB是AC上的中线.
直角三角形斜边上的中线等于斜边的一半.
∵ OB是AC上的中线
直角三角形斜边上的中线定理：
∵ 在Rt△ABC中，点O是斜边AC的中点
(或 OB=OA=OC， 或 AC=2OB )
2.如图，△ABC中，E在AC上，且BE⊥AC．D为AB中点，若DE=5，AE=8，则BE的长为_____．
如图，在矩形ABCD中，AE⊥BD于E，∠DAE:∠BAE＝3:1，求∠BAO和∠EAO的度数．
解:∵ 四边形ABCD是矩形
∴ ∠DAB=90°，AC=BD, OA= AC，OB= BD
∴ ∠DAE+∠BAE=90°，
∵ ∠DAE:∠BAE＝3:1
∴ 设∠DAE＝3x°，
矩形的每条对角线把矩形分成两个直角三角形，矩形的两条对角线将矩形分成四个等腰三角形.因此，有关矩形的计算问题，经常转化到直角三角形和等腰三角形中来解决.
如图，将矩形ABCD沿着直线BD折叠，使点C落在C′处，BC′交AD于点E，AD＝8，AB＝4，求△BED的面积．
解:∵ 四边形ABCD是矩形 ∴ AD∥ BC，∠A＝90° ∴ ∠2＝∠3由折叠知 ∠1＝∠2，∴ ∠1＝∠3，∴ BE＝DE设BE＝DE＝x，则AE＝8-x ∵ 在Rt△ABE中，AB2＋AE2＝BE2 ∴ 42＋(8－x)2＝x2， 解得 x＝5 ，即 DE＝5∴ S△BED＝ DE·AB＝ ×5×4＝10
如图，已知BD，CE是△ABC不同边上的高，点G，F分别是BC，DE的中点，试说明 GF⊥DE.
又∵ 在Rt△BEC中，点G为斜边BC的中点
∵ BD，CE分别为△ABC边上的高
∴ ∠BEC=∠BDC=90°
∵ 在Rt△BDC中，点G为斜边BC的中点
如图，在矩形ABCD中，AB=6，AD=8，P是AD上的动点，PE⊥AC，PF⊥BD于F，求PE+PF的值.
解：连接OP, ∵ 四边形ABCD是矩形
∴ ∠DAB=90°，OA=OB=OC=OD