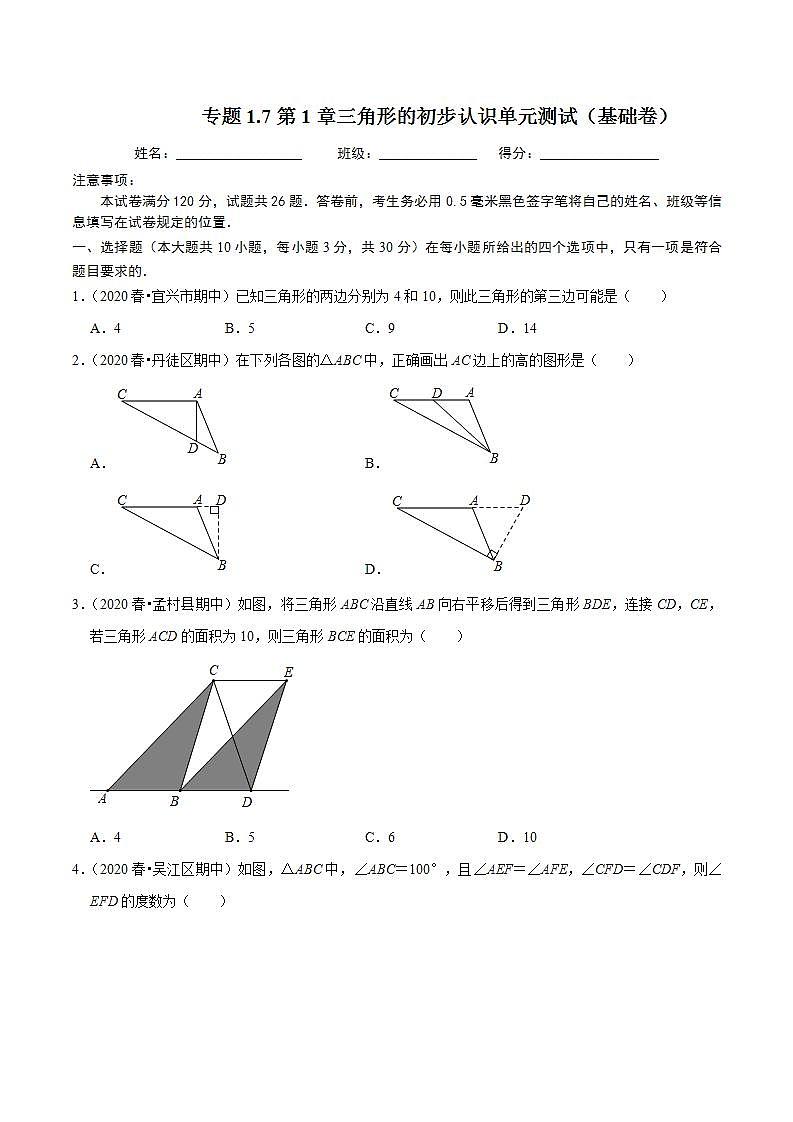
初中数学浙教版八年级上册第1章 三角形的初步知识综合与测试单元测试一课一练

这是一份初中数学浙教版八年级上册第1章 三角形的初步知识综合与测试单元测试一课一练，文件包含浙教版八年级数学上册同步培优练习专题17第1章三角形的初步认识单元测试基础卷详解版docx、浙教版八年级数学上册同步培优练习专题17第1章三角形的初步认识单元测试基础卷测试题docx等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。

 专题1.7第1章三角形的初步认识单元测试（基础卷）
姓名：__________________ 班级：______________ 得分：_________________
注意事项：
本试卷满分100分，试题共24题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2020春•宜兴市期中）已知三角形的两边分别为4和10，则此三角形的第三边可能是（　　）
A．4 B．5 C．9 D．14
【分析】设此三角形第三边的长为x，根据三角形的三边关系求出x的取值范围，找出符合条件的x的值即可．
【解答】解：设此三角形第三边的长为x，则10﹣4＜x＜10+4，即6＜x＜14，四个选项中只有9符合条件．
故选：C．
2．（2020春•丹徒区期中）在下列各图的△ABC中，正确画出AC边上的高的图形是（　　）
A． B．
C． D．
【分析】根据三角形的高的概念判断．
【解答】解：AC边上的高就是过B作垂线垂直AC交AC的延长线于D点，因此只有C符合条件，
故选：C．
3．（2020春•孟村县期中）如图，将三角形ABC沿直线AB向右平移后得到三角形BDE，连接CD，CE，若三角形ACD的面积为10，则三角形BCE的面积为（　　）

A．4 B．5 C．6 D．10
【分析】根据平移的性质得到AB＝BD，BC∥DE，利用三角形面积公式得到S△BCD=12S△ACD＝5，然后利用DE∥BC得到S△BCE＝S△BCD＝5．
【解答】解：∵△ABC沿直线AB向右平移后到达△BDE的位置，
∴AB＝BD，BC∥DE，
∴S△ABC＝S△BCD=12S△ACD=12×10＝5，
∵DE∥BC，
∴S△BCE＝S△BCD＝5．
故选：B．
4．（2020春•吴江区期中）如图，△ABC中，∠ABC＝100°，且∠AEF＝∠AFE，∠CFD＝∠CDF，则∠EFD的度数为（　　）

A．80o B．60o C．40o D．20o
【分析】求出∠AFE+∠CFD即可解决问题．
【解答】解：∵∠B＝100°，
∴∠A+∠C＝80°，
∵∠AFE＝∠AEF，∠CFD＝∠CDF，∠A+2∠AFE＝180°，∠C+2∠CFD＝180°，
∴2∠AFE+2∠CFD＝280°，
∴∠AFE+∠CFD＝140°，
∴∠EFD＝180°﹣140°＝40°，
故选：C．
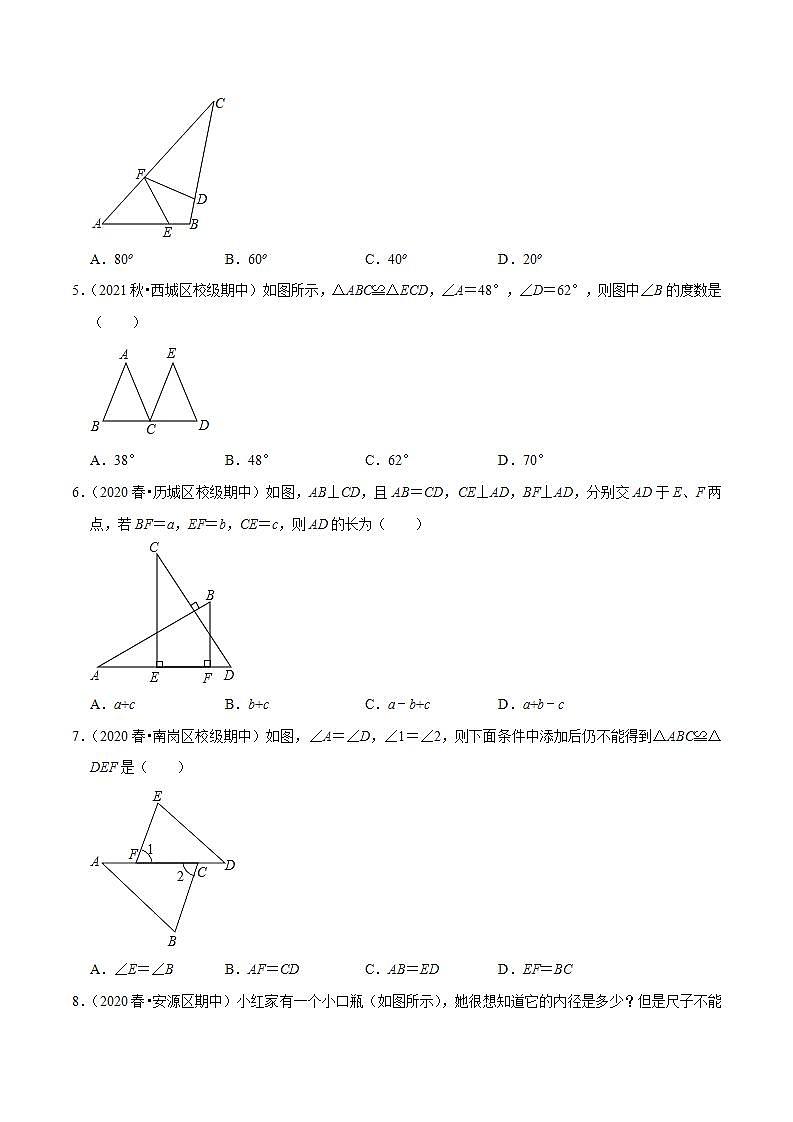
5．（2021秋•西城区校级期中）如图所示，△ABC≌△ECD，∠A＝48°，∠D＝62°，则图中∠B的度数是（　　）

A．38° B．48° C．62° D．70°
【分析】用△ABC≌△ECD求出∠E＝∠A＝48°，再运用三角形内角和求出∠ECD和∠ACB，从而得到结论．
【解答】解：∵△ABC≌△ECD，∠A＝48°，∠D＝62°，点B、C、D在同一直线上
∴∠ACB＝∠D＝62°，
∴∠B＝180°﹣∠A﹣∠ACB＝70°，
故选：D．
6．（2020春•历城区校级期中）如图，AB⊥CD，且AB＝CD，CE⊥AD，BF⊥AD，分别交AD于E、F两点，若BF＝a，EF＝b，CE＝c，则AD的长为（　　）

A．a+c B．b+c C．a﹣b+c D．a+b﹣c
【分析】由余角的性质可得∠A＝∠C，由“AAS”可证△ABF≌△CDE，可得AF＝CE＝c，BF＝DE＝a，可得AD的长．
【解答】解：∵AB⊥CD，CE⊥AD，BF⊥AD，
∴∠AFB＝∠CED＝90°，∠A+∠D＝90°，∠C+∠D＝90°，
∴∠A＝∠C，
∵AB＝CD，∠A＝∠C，∠CED＝∠AFB＝90°
∴△ABF≌△CDE（AAS）
∴AF＝CE＝c，BF＝DE＝a，
∵EF＝b，
∴AD＝AF+DF＝c+（a﹣b）＝a﹣b+c，
故选：C．
7．（2020春•南岗区校级期中）如图，∠A＝∠D，∠1＝∠2，则下面条件中添加后仍不能得到△ABC≌△DEF是（　　）

A．∠E＝∠B B．AF＝CD C．AB＝ED D．EF＝BC
【分析】根据全等三角形的判定定理逐个判断即可．
【解答】解：A、根据∠A＝∠D，∠1＝∠2和∠E＝∠B不符合全等三角形的判定定理，不能推出△ABC≌△DEF，故本选项符合题意；
B、∵AF＝CD，
∴AF+FC＝CD+FC，
即AC＝DF，
在△ABC和△DEF中
∠A=∠DAC=DF∠2=∠1
∴△ABC≌△DEF（ASA），故本选项不符合题意；
C、在△ABC和△DEF中
∠2=∠1∠A=∠DAB=DE
∴△ABC≌△DEF（AAS），故本选项不符合题意；
D、在△ABC和△DEF中
∠2=∠1∠A=∠DBC=EF
∴△ABC≌△DEF（AAS），故本选项不符合题意；
故选：A．
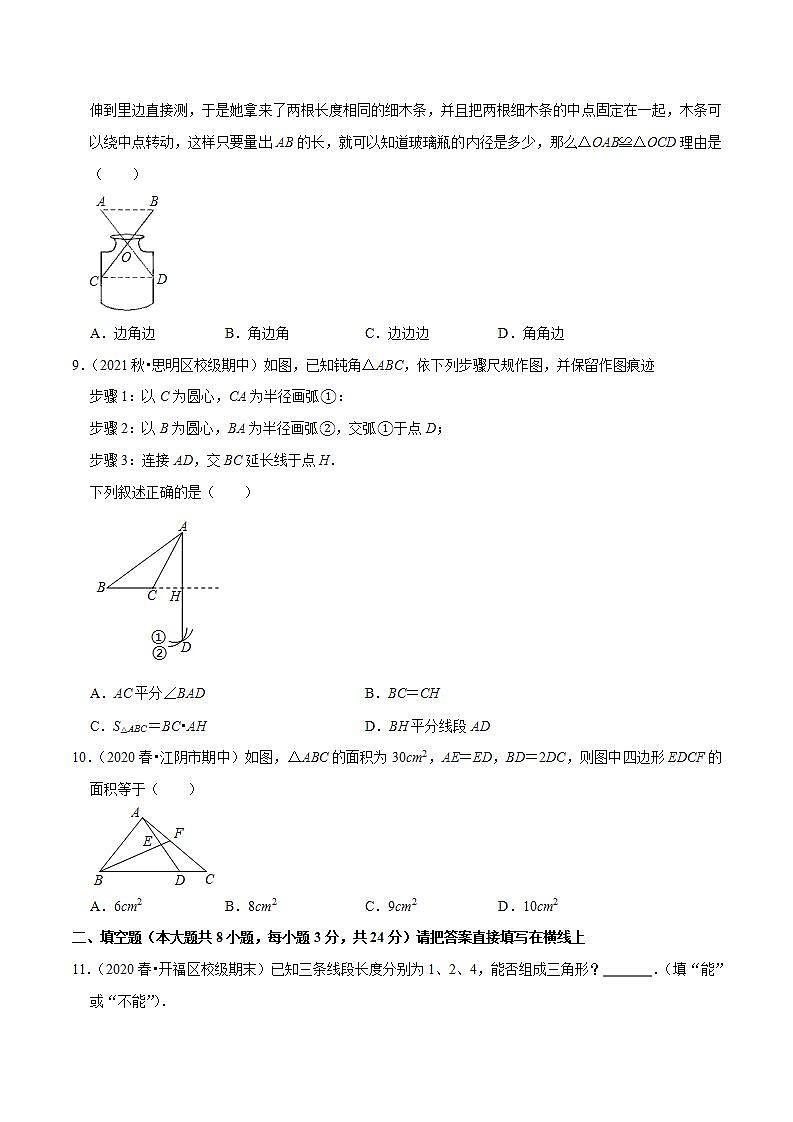
8．（2020春•安源区期中）小红家有一个小口瓶（如图所示），她很想知道它的内径是多少？但是尺子不能伸到里边直接测，于是她拿来了两根长度相同的细木条，并且把两根细木条的中点固定在一起，木条可以绕中点转动，这样只要量出AB的长，就可以知道玻璃瓶的内径是多少，那么△OAB≌△OCD理由是（　　）

A．边角边 B．角边角 C．边边边 D．角角边
【分析】根据题干中给出描述可得AO＝OD，BO＝OC，再根据对顶角相等可得∠AOB＝∠COD，即可解题．
【解答】证明：在△AOB和△COD中，
AO=OD∠AOB=∠CODBO=OC，
∴△AOB≌△COD（SAS），
∴AB＝CD．
故选：A．
9．（2021秋•思明区校级期中）如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹
步骤1：以C为圆心，CA为半径画弧①：
步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；
步骤3：连接AD，交BC延长线于点H．
下列叙述正确的是（　　）

A．AC平分∠BAD B．BC＝CH
C．S△ABC＝BC•AH D．BH平分线段AD
【分析】根据作图过程可得BH是线段AD的垂直平分线即可判断．
【解答】解：根据作图可知：

∴连接CD，BD，
AC＝CD，AB＝DB，
∴BH是AD的垂直平分线，
∴BH平分线段AD．
故选：D．
10．（2020春•江阴市期中）如图，△ABC的面积为30cm2，AE＝ED，BD＝2DC，则图中四边形EDCF的面积等于（　　）

A．6cm2 B．8cm2 C．9cm2 D．10cm2
【分析】连接DF．可知三角形AEF的面积等于三角形EFD的面积，三角形ABE的面积等于三角形BED的面积，三角形BDF的面积等于三角形FDC的面积的2倍．通过各个面积之间的关系，求出各自区域的面积即可得出所求面积．
【解答】解：如图，连接DF，
∵AE＝ED，BD＝2DC，
∴△AEF的面积等于△EFD的面积，△ABE的面积等于△BED的面积，△BDF的面积等于△FDC的面积的2倍，△ABD的面积等于△ADC面积的2倍．
设△AEF面积为x，△BDE面积为y，
则x+x+y+y+12（x+y）＝30；①
2y＝2[2x+12(x+y)]②
得出x+y＝12．
解得x＝2．y＝10，
故四边形CDEF的面积等于x+12（x+y）＝8cm2，
故选：B．
二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
11．（2020春•开福区校级期末）已知三条线段长度分别为1、2、4，能否组成三角形？　不能　．（填“能”或“不能”）．
【分析】根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”进行分析．
【解答】解：根据三角形的三边关系，1+2＝3＜4，不能组成三角形；
故答案为：不能．
12．（2020春•东海县期末）命题“末尾数字是5的数，能被5整除．”的逆命题是　能被5整除的数，末尾数字都是5　．
【分析】交换原命题的题设与结论得到它的逆命题．
【解答】解：命题“末尾数字是5的数，能被5整除．”的逆命题是能被5整除的数，末尾数字都是5．
故答案为能被5整除的数，末尾数字都是5．
13．（2020春•鼓楼区期末）如图，直线a、b、c、d互不平行，以下结论正确的是　①②③　．（只填序号）
①∠1+∠2＝∠5；
②∠1+∠3＝∠4；
③∠1+∠2+∠3＝∠6；
④∠3+∠4＝∠2+∠5．

【分析】利用三角形的外角的性质求解即可．
【解答】解：由三角形外角的性质可知：∠5＝∠1+∠2，∠4＝∠1+∠3，∠6＝∠4+∠2＝∠3+∠5，
∴∠6＝∠1+∠2+∠3，
故①②③正确，
故答案为①②③．
14．（2020春•雅安期末）如图，在△ABC中，D、E分别是AC，AB上的点，若△ADE≌△BDE≌△BDC，则∠DBC的度数为　30°　．

【分析】根据全等三角形的性质得出∠A＝∠DBE＝∠CBD，∠C＝∠AED＝∠BED，根据邻补角互补求出∠AED＝∠BED＝90°＝∠C，再根据三角形内角和定理求出即可．
【解答】解：∵△ADE≌△BDE≌△BDC，
∴∠A＝∠DBE＝∠CBD，∠C＝∠AED＝∠BED，
∵∠AED+∠BED＝180°，
∴∠AED＝∠BED＝90°＝∠C，
∵∠C+∠A+∠CBA＝180°，
∴3∠A＝90°，
∴∠A＝30°，
∴∠DBC＝∠A＝30°，
故答案为：30°．
15．（2020春•郑州期末）如图△ABC≌△EFD，请写出一组图中平行的线段　AB∥FE，答案不唯一　．

【分析】根据全等三角形的性质和平行线的判定解答即可．
【解答】解：∵△ABC≌△EFD，
∴∠B＝∠F，∠ACB＝∠EDF，
∴AB∥EF，AC∥DE，
故答案为：AB∥FE，答案不唯一．
16．（2020春•松北区期末）如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝20°，∠2＝25°，则∠3＝　45°　．

【分析】根据等式的性质得出∠BAD＝∠CAE，再利用全等三角形的判定和性质解答即可．
【解答】解：∵∠BAC＝∠DAE，
∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，
即∠BAD＝∠CAE，
在△BAD与△CAE中，
AB=AC∠BAD=∠CAEAD=AE，
∴△BAD≌△CAE（SAS），
∴∠ABD＝∠2＝25°，
∴∠3＝∠1+∠ABD＝25°+20°＝45°．
故答案为：45°．
17．（2020春•宁德期末）如图，已知△ABC，∠C＝90°，BD是△ABC的角平分线，若AD＝3，CD＝2，则点D到AB边的距离为　2　．

【分析】过点D作DE⊥AB于E，先求出CD，再根据角平分线上的点到角的两边的距离相等可得DE＝CD，即可得解．
【解答】解：如图，过点D作DE⊥AB于E，
∵∠C＝90°，BD是三角形的角平分线，
∴DE＝CD＝2，
即点D到AB边的距离是2．
故答案为：2．

18．（2020•东城区二模）如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC＝6cm，AC＝5cm，则△ACE的周长为　11　cm．

【分析】根据ED垂直平分AB，可以得到EA＝EC，然后即可得到EA+EC的长等于BC的长，从而可以求得△AEC的周长．
【解答】解：∵ED垂直平分AB，
∴EA＝EB，
∵BC＝6cm，AC＝5cm，
∴EB+EC＝6cm，
∴EA+EC＝6cm，
∴EA+EC+AC＝6+5＝11cm，
即△ACE的周长是11cm，
故答案为：11．
三、解答题（本大题共8小题，共66分．解答时应写出文字说明、证明过程或演算步骤）
19．（2020春•溧水区期末）如图，BD为△ABC的角平分线，若∠ABC＝60°，∠ADB＝70°．
（1）求∠C的度数；
（2）若点E为线段BC上任意一点，当△DEC为直角三角形时，则∠EDC的度数
为　50°或90°　．

【分析】（1）利用角平分线的性质可得∠DBC＝30°，由外角的性质可得结果；
（2）利用分类讨论思想：如图1，则∠CDE＝90°；如图2，当∠CED＝90°时，则∠EDC＝90°﹣∠C＝90°﹣40°＝50°．
【解答】解：（1）∵BD为△ABC的角平分线，∠ABC＝60°
∴∠DBC=12∠ABC＝30°，
又∵∠ADB是△BDC的外角，∠ADB＝70°，
∴∠ADB＝∠DBC+∠C，
∴∠C＝∠ADB﹣∠DBC＝40°；

（2）情况一，如图1，

则∠CDE＝90°；
情况二：如图2，当∠CED＝90°时，

∠EDC＝90°﹣∠C＝90°﹣40°＝50°，
综上所述，∠EDC的度数为90°或50°，
故答案为：50°或90°．
20．（2020春•朝阳区校级期末）如图，在△ABC中，∠B＝25°，∠BAC＝31°，过点A作BC边上的高，交BC的延长线于点D，CE平分∠ACD，交AD于点E．
求：（1）∠ACD的度数；
（2）∠AEC的度数．

【分析】（1）利用三角形的外角的性质求解即可．
（2）求出∠ECD，∠D，利用三角形的外角的性质求解即可．
【解答】解：（1）∵∠ACD＝∠B+∠BAC，∠B＝25°，∠BAC＝31°，
∴∠ACD＝25°+31°＝56°．

（2）∵AD⊥BD，
∴∠D＝90°，
∵∠ACD＝56°，CE平分∠ACD，
∴∠ECD=12∠ACD＝28°，
∴∠AEC＝∠ECD+∠D＝28°+90°＝118°．
21．（2020春•裕华区校级期末）（1）已知△ABC中，∠B＞∠C，AD⊥BC于D，AE平分∠BAC，∠B＝70°，∠C＝40°，求∠DAE的度数．
（2）在图2中，∠B＝x，∠C＝y，其他条件不变，若把“AD⊥BC于D改为“F是AE上一点，FD⊥BC于D“，试用x、y表示∠DFE＝　12（x﹣y）　：
（3）在图3中，若把（2）中的“点F在AE上“改为点F是AE延长线上一点”，其余条件不变，试用x、y表示∠DFE＝　12（x﹣y）　；
（4）在图3中，分别作出∠BAE和∠EDF的角平分线，交于点P，如图4．试用x、y表示∠P＝　14（3x﹣y）　．

【分析】（1）首先利用三角形内角和定理可求出∠BAC的度数，进而可求出∠BAD的度数，由垂直可得∠BAE＝90°﹣x，进而可求∠EAD的度数；
（2）由题意可知∠AEB＝90°−12x+12y，再利用已知条件和直角三角形余角的性质即可求出∠DFE的度数．
（3）由题意可知∠AEB＝90°−12x+12y，再利用已知条件、对顶角的性质和直角三角形余角的性质即可求出∠DFE的度数．
（4）由题意可知∠PAF=14（180°﹣x﹣y），再利用已知条件、对顶角的性质和角平分线的性质即可求出∠P的度数．
【解答】（1）解：∵∠B＝70°，∠C＝40°，
∴∠BAC＝180°﹣70°﹣40°＝70°，
∵∠BAC的平分线交BC于点D，
∴∠BAD=12∠BAC=12×70°＝35°，
在Rt△ABE中，∠BAE＝90°﹣70°＝20°，
∴∠EAD＝∠BAD﹣∠BAE＝35°﹣20°＝15°，
（2）∵∠BAD=12∠BAC=12（180°﹣x﹣y），
∴∠AEB＝180°﹣∠B﹣∠BAD＝180°﹣x−12（180°﹣x﹣y）＝90°−12x+12y，
∴∠DFE＝90°﹣∠AEB＝90°﹣90°+12x−12y=12（x﹣y）．
故答案为12（x﹣y）．
（3）∵∠BAD=12∠BAC=12（180°﹣x﹣y），
∴∠AEB＝180°﹣∠B﹣∠BAD＝180°﹣x−12（180°﹣x﹣y）＝90°−12x+12y，
∴∠DEF＝∠AEB＝90°−12x+12y，
∴∠DFE＝90°﹣∠DEF＝90°﹣90°+12x−12y=12（x﹣y）．
故答案为12（x﹣y）．
（4）∵∠BAD=12∠BAC=12（180°﹣x﹣y），
∴∠PAF=14（180°﹣x﹣y），
∴∠P＝180°﹣45°﹣[180°−14（180°﹣x﹣y）﹣x]=14（3x﹣y）．
故答案为14（3x﹣y）．
22．（2021秋•孝义市期末）已知：如图，△ABC≌△DEF，AM、DN分别是△ABC、△DEF的对应边上的高．求证：AM＝DN．

【分析】根据全等三角形的性质得出AB＝DE，∠E＝∠B，利用AAS证明△ABM与△DEN全等，进而证明即可．
【解答】证明：∵△ABC≌△DEF，
∴AB＝DE，∠B＝∠E，
∵AM，DN分别是△ABC，△DEF的对应边上的高，
即AM⊥BC，DN⊥EF，
∴∠AMB＝∠DNE＝90°，
在△ABM和△DEN中∠AMB=∠DNE∠B=∠EAB=DE，
∴△ABM≌△DEN（AAS），
∴AM＝DN．
23．（2021秋•临泉县期末）如图，△ABC≌△DBE，点D在边AC上，BC与DE交于点P，已知∠ABE＝162°，∠DBC＝30°，求∠CDE的度数．

【分析】根据全等三角形的性质得到∠ABC＝∠DBE，计算即可．
【解答】解：∵∠ABE＝162°，∠DBC＝30°，
∴∠ABD+∠CBE＝132°，
∵△ABC≌△DBE，
∴∠ABC＝∠DBE，∠C＝∠E，
∴∠ABD＝∠CBE＝132°÷2＝66°，
∵∠CPD＝∠BPE，
∴∠CDE＝∠CBE＝66°．
24．（2020•雁塔区校级模拟）如图，点C，D均在线段AB上，且AD＝BC，分别过C、D作FC⊥AB，ED⊥AB，连接AE、BF，连接EF交AB于点G，若AE＝BF，求证：DG＝CG．

【分析】由“HL”可证Rt△ADE≌Rt△BCF，可得DE＝CF，由“AAS”可证△EDG≌△FCG，可得结论．
【解答】证明：∵FC⊥AB，ED⊥AB，
∴∠EDA＝∠FCB＝90°，
在Rt△ADE和Rt△BCF中，
AE=DFAD=BC，
∴Rt△ADE≌Rt△BCF（HL），
∴DE＝CF，
∵∠EGD＝∠FGC，∠EDG＝∠FCG＝90°，
∴△EDG≌△FCG（AAS）
∴DG＝CG．

25．（2020春•南岸区期末）如图，在△ABC中，点D是BC上一点，且AD＝AB，AE∥BC，∠BAD＝∠CAE，连接DE交AC于点F．
（1）若∠B＝70°，求∠C的度数；
（2）若AE＝AC，AD平分∠BDE是否成立？请说明理由．

【分析】（1）根据等腰三角形的性质得出∠ADB＝∠B＝70°，根据三角形的内角和定理求出∠BAD＝40°，求出∠CAE＝40°，根据平行线的性质得出即可；
（2）求出∠BAC＝∠DAE，根据全等三角形的判定推出△BAC≌△DAE，根据全等三角形的性质得出∠B＝∠ADE，求出∠ADE＝∠ADB即可．
【解答】解：（1）∵∠B＝70°，AB＝AD，
∴∠ADB＝∠B＝70°，
∵∠B+∠BAD+∠ADB＝180°，
∴∠BAD＝40°，
∵∠CAE＝∠BAD，
∴∠CAE＝40°，
∵AE∥BC，
∴∠C＝∠CAE＝40°；

（2）AD平分∠BDE，
理由是：∵∠BAD＝∠CAE，
∴∠BAD+∠CAD＝∠CAE+∠CAD，
即∠BAC＝∠DAE，
在△BAC和△DAE中，
AB=AD∠BAC=∠DAEAC=AE，
∴△BAC≌△DAE（SAS）
∴∠B＝∠ADE，
∵∠B＝∠ADB，
∴∠ADE＝∠ADB，
即AD平分∠BDE．
26．（2020•河池）（1）如图（1），已知CE与AB交于点E，AC＝BC，∠1＝∠2．求证：△ACE≌△BCE．
（2）如图（2），已知CD的延长线与AB交于点E，AD＝BC，∠3＝∠4．探究AE与BE的数量关系，并说明理由．

【分析】（1）根据SAS可得出答案；
（2）在CE上截取CF＝DE，证明△ADE≌△BCF（SAS），可得出AE＝BF，∠AED＝∠CFB，则可得出BE＝BF．结论得证．
【解答】（1）证明：在△ACE和△BCE中，
∵AC=BC∠1=∠2CE=CE，
∴△ACE≌△BCE（SAS）；
（2）AE＝BE．
理由如下：
在CE上截取CF＝DE，

在△ADE和△BCF中，
∵AD=CB∠3=∠4CF=DE，
∴△ADE≌△BCF（SAS），
∴AE＝BF，∠AED＝∠CFB，
∵∠AED+∠BEF＝180°，∠CFB+∠EFB＝180°，
∴∠BEF＝∠EFB，
∴BE＝BF，
∴AE＝BE．