2020-2021学年3.3 抛物线教课课件ppt

这是一份2020-2021学年3.3 抛物线教课课件ppt，文件包含第二课时抛物线的方程及性质的应用pptx、第二课时抛物线的方程及性质的应用DOCX等2份课件配套教学资源，其中PPT共52页， 欢迎下载使用。
1.了解抛物线的简单应用.2.运用抛物线的方程及简单几何性质，解决与抛物线有关的问题.
通过本节课进一步提升逻辑推理及数学运算素养.
问题导学预习教材必备知识探究
互动合作研析题型关键能力提升
拓展延伸分层精练核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
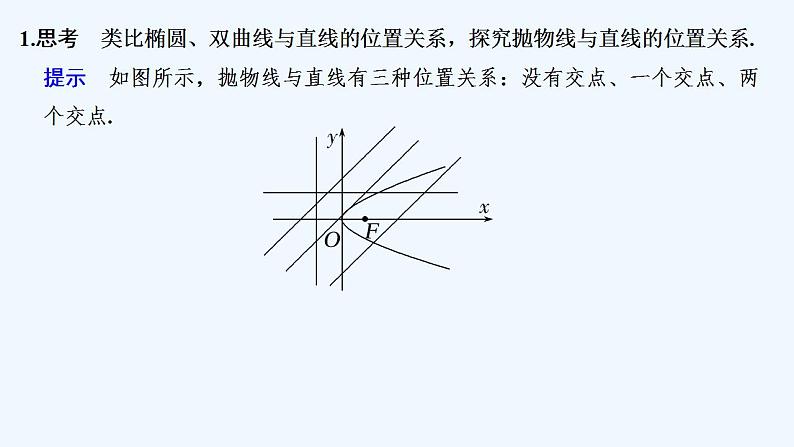
1.思考　类比椭圆、双曲线与直线的位置关系，探究抛物线与直线的位置关系.提示　如图所示，抛物线与直线有三种位置关系：没有交点、一个交点、两个交点.
设直线l：y＝kx＋b，抛物线：y2＝2px(p＞0)，将直线方程与抛物线方程联立消元得：k2x2＋(2kb－2p)x＋b2＝0.①若k2＝0，此时直线与抛物线有一个交点，该直线平行于抛物线的对称轴或与对称轴重合.②若k2≠0，当Δ＞0时，直线与抛物线相交，有两个交点；当Δ＝0时，直线与抛物线相切，有一个交点；当Δ＜0时，直线与抛物线相离，无公共点.
2.填空　(1)直线与抛物线的位置关系的判断方法
温馨提醒　(1)直线与抛物线有一个公共点是直线与抛物线相切的必要不充分条件.(2)研究直线与抛物线的关系时要注意直线斜率不存在的情况.
(1)若一条直线与抛物线只有一个公共点，则二者一定相切.( )提示　结合图象可知当直线与抛物线的对称轴平行时，也只有一个公共点，此时不相切.(2)“直线与抛物线有一个交点”是“直线与抛物线相切”的必要不充分条件. ( )(3)由抛物线y2＝2px(p>0)的图象可知，其上任意一点的横坐标的取值范围是x≥0. ( )(4)抛物线的方程虽然各不相同，但是其离心率都相同. ( )
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
例1 已知抛物线的方程为y2＝4x，直线l过定点P(－2，1)，斜率为k，k为何值时，直线l与抛物线y2＝4x只有一个公共点；有两个公共点；没有公共点？解　由题意，直线l的方程为y－1＝k(x＋2)，
可得ky2－4y＋4(2k＋1)＝0.①当k＝0时，由方程①得y＝1，
判断直线与抛物线的位置关系的方法：联立方程组消元，当二次项系数不等于零时，用判别式Δ来判定，当二次项系数等于0时，直线与抛物线相交于一点.
训练1 (1)已知直线y＝kx－k及抛物线y2＝2px(p＞0)，则(　　)A.直线与抛物线有一个公共点B.直线与抛物线有两个公共点C.直线与抛物线有一个或两个公共点D.直线与抛物线可能没有公共点
解析　∵直线y＝kx－k＝k(x－1)，∴直线过点(1，0).又点(1，0)在抛物线y2＝2px的内部，∴当k＝0时，直线与抛物线有一个公共点；当k≠0时，直线与抛物线有两个公共点.
将直线l的方程与y2＝2px联立，消去x得ky2－2py＋(2＋3k)p2＝0.
2x－6y＋9p＝0或2x＋2y＋p＝0或y＝p
所以直线l的方程为2x－6y＋9p＝0或2x＋2y＋p＝0.当直线l与x轴平行时，直线l与抛物线只有一个交点，此时，y＝p.故满足条件的直线共有三条，其方程为2x－6y＋9p＝0或2x＋2y＋p＝0或y＝p.
例2 过点P(4，1)作抛物线y2＝8x的弦AB，弦AB恰被点P平分，求AB所在直线的方程及弦AB的长度.
两式相减，得(y1－y2)(y1＋y2)＝8(x1－x2).∵P是AB的中点，∴x1＋x2＝8，y1＋y2＝2，
∴所求直线AB的方程为y－1＝4(x－4)，即4x－y－15＝0.
法二　由题意知AB所在直线的斜率存在且不为0.设AB所在直线的方程为y＝k(x－4)＋1(k≠0)，
涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”“整体代入”等解法.注意：涉及弦的中点、斜率时一般用“点差法”求解.
解析　由题意知，抛物线的焦点坐标为(2，0)，直线l过焦点F，
(2)已知抛物线C的顶点在坐标原点，焦点为F(1，0).直线l与抛物线C相交于A，B两点，若AB的中点为(2，2)，则抛物线的方程为________，直线l的方程为________.
解析　由题意知抛物线的方程为y2＝4x，设直线l与抛物线C的交点为A(x1，y1)，B(x2，y2)，
因为AB的中点为(2，2)，所以y1＋y2＝4，
所以直线l的方程为y－2＝x－2，即x－y＝0.
解　过点P作x轴的垂线且垂足为点N，则|PN|＝y，
化简得x2＝2y.故点P的轨迹方程为x2＝2y.
消去y化简得x2－2kx－2＝0，∴x1＋x2＝2k，x1x2＝－2.
∴k4＋3k2－4＝0，又k2≥0，∴k2＝1，∴k＝±1.
求轨迹问题的两种方法(1)直接法：按照动点适合条件直接代入求方程.(2)定义法：若动点满足某种曲线定义，可按待定系数法列方程(组)求解曲线方程.
训练3 若动圆M与圆C：(x－2)2＋y2＝1外切，又与直线x＋1＝0相切，求动圆圆心的轨迹方程.解　设动圆圆心为M(x，y)，半径为R，由已知可得定圆圆心为C(2，0)，半径r＝1.因为两圆外切，所以|MC|＝R＋1.又动圆M与已知直线x＋1＝0相切，所以圆心M到直线x＋1＝0的距离d＝R.所以|MC|＝d＋1.即动点M到定点C(2，0)的距离等于它到定直线x＋2＝0的距离.
由抛物线的定义可知，点M的轨迹是以C为焦点，x＝－2为准线的抛物线，
故动圆圆心M的轨迹方程为y2＝8x.
1.重要思想与方法(1)直线与抛物线的位置关系：①相离；②相切；③相交.(2)直线与抛物线的相交弦问题，大多涉及抛物线的弦长、弦的中点、弦的斜率.常用的办法是将直线方程与抛物线方程联立，转化为关于x或y的一元二次方程，然后利用根与系数的关系，这样避免求交点.尤其是弦的中点问题，还应注意“点差法”的运用.(3)本节课应用数学思想方法有：点差法、数形结合法和转化法.2.易错易混点提醒(1)利用点差法求轨迹方程时注意x或y的取值范围.(2)直线方程y＝kx＋b中k＝0时，与抛物线y2＝2px(p＞0)只有一个交点.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
1.动点P(x，y)到点F(3，0)的距离比它到直线x＋2＝0的距离大1，则动点的轨迹是(　　)A.椭圆 B.双曲线 C.双曲线的一支 D.抛物线
解析　依题意可知动点P(x，y)在直线x＋2＝0的右侧，设P到直线x＋2＝0的距离为d，则|PF|＝d＋1，所以动点P到F(3，0)的距与到x＋3＝0的距离相等，其轨迹为抛物线.
2.已知直线l与抛物线x2＝2py(p＞0)只有一个交点，则直线l与抛物线的位置关系是(　　)A.相交 B.相切C.相离 D.相交或相切 解析　当直线l与y轴平行或重合时，直线l与抛物线x2＝2py(p＞0)有一个交点，此时直线l与抛物线是相交的.当直线l的斜率存在，直线l与抛物线x2＝2py(p＞0)只有一个交点时，直线l与抛物线相切.
消去y并整理得2x2－11x＋8＝0，Δ＞0，设A(x1，y1)，B(x2，y2)，
4.已知抛物线y＝4x2上一点到直线y＝4x－5的距离最短，则该点的坐标是(　　)
解析　法一　设抛物线上点的坐标为(x，4x2)，其中x∈R，由点到直线的距离公式得
法二　设与y＝4x－5平行的抛物线y＝4x2的切线方程为y＝4x＋m，
再由Δ＝16－4×4·(－m)＝0，得m＝－1.
6.直线y＝kx＋2与抛物线y2＝8x有且只有一个公共点，则k＝________.
解析　当k＝0时，直线与抛物线有唯一交点；当k≠0时，联立方程消去y得k2x2＋4(k－2)x＋4＝0，由题意Δ＝16(k－2)2－16k2＝0，所以k＝1.综上，k＝0或k＝1.
7.直线y＝x－1被抛物线y2＝4x截得的线段的中点坐标是________.
解析　设线段的端点为(x1，y1)，(x2，y2)，将y＝x－1代入y2＝4x，整理得x2－6x＋1＝0.由根与系数的关系，得
∴所求点的坐标为(3，2).
解　设抛物线的方程为y2＝2ax(a≠0)，
得4x2－(2a－4)x＋1＝0.设直线y＝2x＋1与抛物线交于A，B两点，其坐标为A(x1，y1)，B(x2，y2)，则
解得a＝－2或a＝6(经检验均满足Δ＝(2a－4)2－4×4>0).∴抛物线方程为y2＝－4x或y2＝12x.
10.已知抛物线C：x2＝－2py(p>0)经过点(2，－1).(1)求抛物线C的方程及其准线方程.
解　由抛物线C：x2＝－2py经过点(2，－1)得p＝2.所以抛物线C的方程为x2＝－4y，其准线方程为y＝1.
(2)设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M，N，直线y＝－1分别交直线OM，ON于点A和点B.求证：以AB为直径的圆经过y轴上的两个定点.
证明　抛物线C的焦点为F(0，－1).设直线l的方程为y＝kx－1(k≠0).
设M(x1，y1)，N(x2，y2)，则x1x2＝－4.
综上，以AB为直径的圆经过y轴上的定点(0，1)和(0，－3).
11.设抛物线y2＝4x上一点P到y轴的距离为d1，到直线l：3x＋4y＋12＝0的距离为d2，则d1＋d2的最小值为(　　)
得3y2＋16y＋48＝0，Δ＝256－12×48＜0，故方程无解，∴直线3x＋4y＋12＝0与抛物线相离.又d1＋d2＝d1＋1＋d2－1，
而d1＋1为P到准线x＝－1的距离，故d1＋1为P到焦点F(1，0)的距离，从而 d1＋1＋d2的最小值为F到直线3x＋4y＋12＝0的距离，
故d1＋d2的最小值为2.
12.已知点M(－1，1)和抛物线C：y2＝4x，过C的焦点且斜率为k的直线与C交于A，B两点.若∠AMB＝90°，则k＝________.
解析　由抛物线的方程y2＝4x可知其焦点F的坐标为(1，0)，所以直线AB的方程为y＝k(x－1)，
得k2x2－2(k2＋2)x＋k2＝0，设A(x1，y1)，B(x2，y2)，
13.已知点A，B关于坐标原点O对称，|AB|＝4，⊙M过点A，B且与直线x＋2＝0相切.(1)若A在直线x＋y＝0上，求⊙M的半径；
解　因为⊙M过点A，B，所以圆心M在AB的垂直平分线上.由已知A在直线x＋y＝0上，且A，B关于坐标原点O对称，所以M在直线y＝x上，故可设M(a，a).因为⊙M与直线x＋2＝0相切，所以⊙M的半径为r＝|a＋2|.
故可得2a2＋4＝(a＋2)2，解得a＝0或a＝4.故⊙M的半径r＝2或r＝6.
(2)是否存在定点P，使得当A运动时，|MA|－|MP|为定值？并说明理由.
解　存在定点P(1，0)，使得|MA|－|MP|为定值.理由如下：设M(x，y)，由已知得⊙M的半径为r＝|x＋2|，|AO|＝2.
故可得x2＋y2＋4＝(x＋2)2，化简得M的轨迹方程为y2＝4x.因为曲线C：y2＝4x是以点P(1，0)为焦点，以直线x＝－1为准线的抛物线，所以|MP|＝x＋1.因为|MA|－|MP|＝r－|MP|＝x＋2－(x＋1)＝1，所以存在满足条件的定点P.
14.抛物线有如下光学性质：由其焦点射出的光线经抛物线反射后，沿平行于抛物线对称轴的方向射出.今有抛物线y2＝2px(p＞0)，如图，一平行于x轴的光线射向抛物线上的点P，反射后又射向抛物线上的点Q，再反射后又沿平行于x轴的方向射出，且两平行光线间的最小距离为3，则抛物线的方程为_____________.
当直线PQ的斜率不存在时，易得|PQ|＝2p；当直线PQ的斜率存在时，
综上，当直线PQ与x轴垂直时，弦长最短，又因为两平行光线间的最小距离为3，故2p＝3，所以抛物线的方程为y2＝3x.