【最新版】高中数学（新人教A版）习题+同步课件章末复习提升

这是一份【最新版】高中数学（新人教A版）习题+同步课件章末复习提升，文件包含章末复习提升pptx、章末复习提升DOCX等2份课件配套教学资源，其中PPT共48页， 欢迎下载使用。


章末复习提升
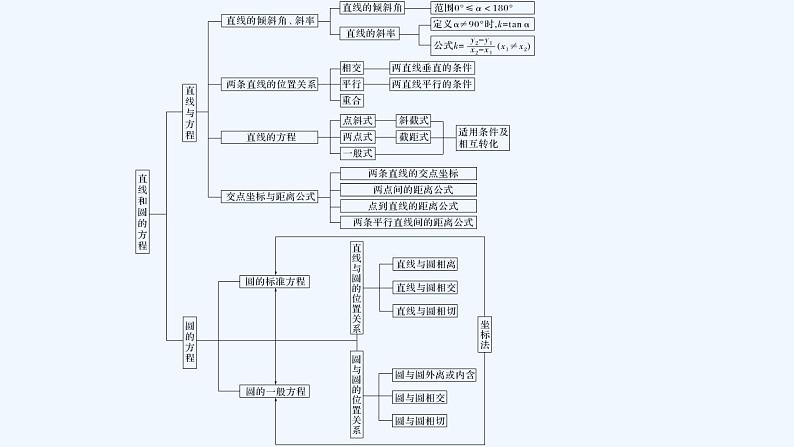
第二章　直线和圆的方程
网络构建形成体系
内容索引
要点聚焦类型突破
WANG LUO GOU JIAN XING CHENG TI XI
网络构建 形成体系
1
2
YAO DIAN JU JIAO LEI XING TU PO
要点聚焦 类型突破
求直线方程的一种重要方法就是待定系数法.运用此方法，要注意各种形式的方程的适用条件，选择适当的直线方程的形式至关重要.
例1 在平面直角坐标系中，已知△ABC的顶点A(0，1)，B(3，2). (1)若C点坐标为(1，0)，求AB边上的高所在的直线方程；
解　∵A(0，1)，B(3，2)，
由垂直关系可得AB边上的高所在的直线的斜率为k＝－3，∴AB边上的高所在直线方程为y－0＝－3(x－1)，化为一般式可得3x＋y－3＝0.
(2)若点M(1，1)为边AC的中点，求边BC所在的直线方程.
解　∵M(1，1)为AC的中点，A(0，1)，
∴边BC所在直线方程为y－1＝x－2，化为一般式可得x－y－1＝0.
训练1 已知△ABC的顶点A(6，1)，AB边上的中线CM所在直线方程2x－y－5＝0，AC边上的高BH所在直线方程为x－2y－5＝0.求： (1)顶点C的坐标；
(2)直线BC的方程.
解决此类问题关键是掌握两条直线平行与垂直的判定：若两条不重合的直线l1，l2的斜率k1，k2存在，则l1∥l2⇔k1＝k2，l1⊥l2⇔k1k2＝－1.若给出的直线方程中存在字母系数，则要考虑斜率是否存在.对于两条直线平行的问题，要注意排除两条直线重合的可能性.
例2 (1)当a＝_______时，直线l1：y＝－x＋2a与直线l2：y＝(a2－2)x＋2平行；
－1
解析　直线l1的斜率k1＝－1，直线l2的斜率k2＝a2－2.因为l1∥l2，所以a2－2＝－1且2a≠2，解得a＝－1.所以当a＝－1时，直线l1：y＝－x＋2a与直线l2：y＝(a2－2)x＋2平行.
(2)当a＝__________时，直线l1：y＝(2a－1)x＋3与直线l2：y＝4x－3垂直.
解析　直线l1的斜率k1＝2a－1，l2的斜率k2＝4.因为l1⊥l2，所以k1·k2＝－1，即4(2a－1)＝－1，
训练2 (1)已知直线l1：ax－3y＋1＝0，l2：2x＋(a＋1)y＋1＝0.若l1⊥l2，则实数a的值等于________； (2)已知直角三角形ABC的直角顶点C(1，1)，点A(－2，3)，B(0，y)，则y＝____.
－3
解析　(1)∵直线l1：ax－3y＋1＝0，l2：2x＋(a＋1)y＋1＝0，且l1⊥l2，∴2a－3(a＋1)＝0，∴a＝－3.
∵∠C＝90°，∴AC⊥BC，
解决解析几何中的距离问题时，往往是代数运算与几何图形直观分析相结合.三种距离是高考考查的热点，公式如下表：
1.关于点的对称问题
(2)直线关于点的对称问题：若两条直线l1，l2关于点P对称，则：①l1上任意一点关于点P的对称点必在l2上，反过来，l2上任意一点关于点P的对称点必在l1上；②若l1∥l2，则点P到直线l1，l2的距离相等；③过点P作一直线与l1，l2分别交于A，B两点，则点P是线段AB的中点.
2.关于直线的对称问题
(1)点关于直线的对称问题：若A，B两点关于直线l对称，则l是线段AB的垂直平分线.①直线AB与直线l垂直；②线段AB的中点在直线l上；③直线l上任意一点到A，B两点的距离相等.(2)直线关于直线的对称问题：若两条直线l1，l2关于直线l对称，则①l1上任意一点关于直线l的对称点必在l2上，反过来，l2上任意一点关于直线l的对称点必在l1上；②过直线l上的一点P且垂直于直线l作一直线与l1，l2分别交于A，B两点，则点P是线段AB的中点.
例4 已知直线l：y＝3x＋3，求： (1)点P(4，5)关于l的对称点坐标；
解　设点P关于直线l的对称点为P′(x′，y′)，则线段PP′的中点M在直线l上，且直线PP′垂直于直线l，
∴P′点坐标为(－2，7).
(2)直线y＝x－2关于l的对称直线的方程；
(3)直线l关于点A(3，2)的对称直线的方程.
训练4 已知直线l：2x－3y＋1＝0，点A(－1，－2).求： (1)点A关于直线l的对称点A′的坐标；
(2)直线m：3x－2y－6＝0关于直线l的对称直线m′的方程；
解　在直线m上取一点，如M(2，0)，则M(2，0)关于直线l的对称点M′必在m′上.设M′(a，b)，
设m与l的交点为N，则由
又∵m′经过点N(4，3)，∴由两点式得直线方程为9x－46y＋102＝0，即为所求直线方程.
(3)直线l关于点A(－1，－2)对称的直线l′的方程.
解　设P(x，y)为l′上任意一点，则P(x，y)关于点A(－1，－2)的对称点为P′(－2－x，－4－y).∵P′在直线l上，∴2(－2－x)－3(－4－y)＋1＝0，即2x－3y－9＝0，即为所求直线方程.
求圆的方程是考查圆的方程问题中的一个基本点，一般涉及圆的性质、直线与圆的位置关系等，主要依据圆的标准方程、一般方程、直线与圆的几何性质，运用几何方法或代数方法解决问题，多以选择题、填空题为主，属于基础题.(1)圆的方程中有三个参数，即标准方程中的a，b，r，或一般式方程中的D，E，F，因此需要三个独立条件建立方程组求解.(2)求圆的方程时，首选几何法，即先分析给出的条件的几何意义，或直接利用待定系数法求解.
解　由x2＋y2－2x＝0得(x－1)2＋y2＝1，故其圆心为(1，0)，半径为1.∵圆C与圆x2＋y2－2x＝0相外切，故两个圆心之间的距离等于半径的和，
设圆C的圆心为(a，b)，半径为r，
训练5 已知直线l经过两条直线2x－y－3＝0和4x－3y－5＝0的交点，且与直线x＋y－2＝0垂直. (1)求直线l的方程；
∵l与x＋y－2＝0垂直，∴kl＝1.又∵l过点(2，1)，∴l的方程y－1＝x－2即x－y－1＝0.
解得a＝3，r＝2.∴圆C的标准方程为(x－3)2＋y2＝4.
圆具有许多重要的几何性质，如圆的切线垂直于经过切点的半径；圆心与弦的中点的连线垂直于弦；切线长定理；直径所对的圆周角是直角等.充分利用圆的几何性质可获得解题途径，减少运算量.另外，对于未给出图形的题目，要边读题边画图，这样能更好地体会圆的几何形状，有助于找到解题思路.
例6 有一个圆与直线l：4x－3y＋6＝0相切于点A(3，6)，且经过点B(5，2)，求此圆的标准方程. 解　设圆心为C，则CA⊥l. 又设直线CA与圆的另一个交点为P.
解　由x2＋y2＋4x－12y＋24＝0得(x＋2)2＋(y－6)2＝42，∴圆C的圆心为C(－2，6)，半径r＝4.如图所示，
在Rt△ACD中，可得|CD|＝2.设所求直线l的斜率为k，则直线l的方程为y－5＝kx，即kx－y＋5＝0.
由点C到直线AB的距离
此时直线l的方程为3x－4y＋20＝0，又∵直线l的斜率不存在时，其方程为x＝0，易知也满足题意.∴所求直线l的方程为x＝0或3x－4y＋20＝0.
(2)求x－2y的最大、最小值.
训练7 已知实数x，y满足方程(x－3)2＋(y－3)2＝6，求x＋y的最大值和最小值.