高中数学人教B版 (2019)选择性必修 第一册1.2.1 空间中的点、直线与空间向量课文内容课件ppt

这是一份高中数学人教B版 (2019)选择性必修 第一册1.2.1 空间中的点、直线与空间向量课文内容课件ppt，文件包含第三课时直线与椭圆的位置关系pptx、第三课时直线与椭圆的位置关系DOCX等2份课件配套教学资源，其中PPT共42页， 欢迎下载使用。

互动合作研析题型关键能力提升
拓展延伸分层精练核心素养达成
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
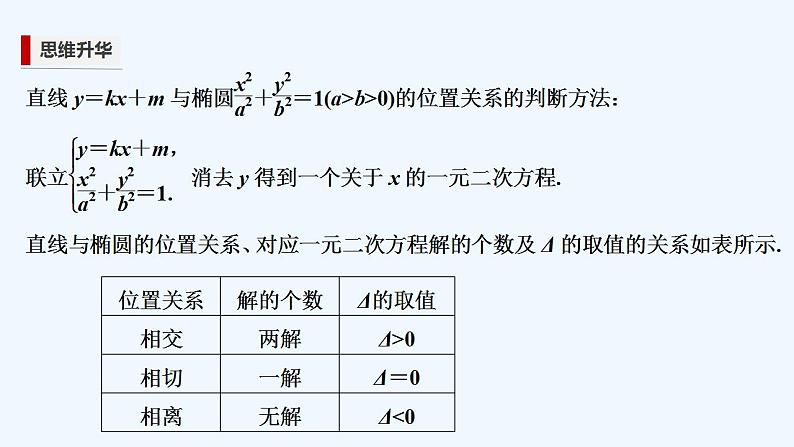
题型一　直线与椭圆的位置关系
解析　法一　由于直线y＝kx＋1恒过点(0，1)，所以点(0，1)必在椭圆内或椭圆上，
消去y整理得(5k2＋m)x2＋10kx＋5(1－m)＝0.由题意知Δ＝100k2－20(1－m)(5k2＋m)≥0对一切k∈R恒成立，即5mk2＋m2－m≥0对一切k∈R恒成立，由于m>0且m≠5，∴m≥1且m≠5.
解　设直线l与曲线C的交点为M(x1，y1)，N(x2，y2)，
整理得k4＋k2－2＝0，解得k2＝1或k2＝－2(舍).∴k＝±1，经检验符合题意.∴直线l的方程是y＝±x＋1，即x－y＋1＝0或x＋y－1＝0.
题型三　直线与椭圆的综合应用
解　存在.当直线l与x轴垂直时不满足条件.故可设A(x1，y1)，B(x2，y2)，直线l的方程为y＝k(x－2)＋1，代入椭圆方程得(3＋4k2)x2－8k(2k－1)x＋16k2－16k－8＝0，
∴4(x1－2)(x2－2)(1＋k2)＝5，
即4[x1x2－2(x1＋x2)＋4](1＋k2)＝5，
“设而不求”法解决直线与椭圆的综合问题可以降低解题难度，提高效率，解题时充分利用几何条件，并将其转化为坐标间的关系，利用x1＋x2，x1·x2的值解题.
由题意知OA⊥OB，则x1x2＋y1y2＝0，
解决直线与椭圆的位置关系问题，经常利用设而不求的方法，解题步骤为：(1)设直线与椭圆的交点为A(x1，y1)，B(x2，y2)；(2)联立直线与椭圆的方程；(3)消元得到关于x或y的一元二次方程；(4)利用根与系数的关系设而不求；(5)把题干中的条件转化为x1＋x2，x1·x2或y1＋y2，y1·y2，进而求解.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
∵Δ＝(－24)2－4×5×32＝－64<0，∴直线与椭圆相离.
7.已知椭圆4x2＋y2＝1及直线y＝x＋m，当直线与椭圆有公共点时，实数m的取值范围是________________.
当直线与椭圆有公共点时，Δ＝4m2－4×5(m2－1)≥0，
设直线与椭圆的交点为A(x1，y1)，B(x2，y2)，
由椭圆的定义，得|AF1|＋|AF2|＝2a＝4，|BF1|＋|BF2|＝2a＝4，又|AF1|＋|BF1|＝|AB|，∴△ABF2的周长为|AB|＋|AF2|＋|BF2|＝4a＝8.
设A(x1，y1)，B(x2，y2)，故直线AB的方程为y＝x＋1，
即(m＋n)x2－2nx＋n－1＝0，设M(x1，y1)，N(x2，y2)，MN的中点P(x0，y0)，
∴a2＝2b2，∴c2＝a2－b2＝b2＝9，
∴m＝1或m＝－1(舍去)，直线EF的方程为x＝y－1，即x－y＋1＝0.
直线PQ的方程为x＝my－2；当m＝0时，直线PQ的方程为x＝－2，也符合方程x＝my－2.设P(x1，y1)，Q(x2，y2)，将直线PQ的方程与椭圆C的方程联立，