高中数学苏教版 (2019)选择性必修第一册3.3 抛物线集体备课课件ppt

这是一份高中数学苏教版 (2019)选择性必修第一册3.3 抛物线集体备课课件ppt，文件包含第二课时抛物线的方程与性质的应用pptx、第二课时抛物线的方程与性质的应用doc等2份课件配套教学资源，其中PPT共56页， 欢迎下载使用。

第3章 圆锥曲线与方程
第二课时　抛物线的方程与性质的应用
课标要求
1.了解抛物线的简单应用.2.能运用抛物线的方程及简单几何性质，解决与抛物线有关的问题.
素养要求
通过本节课进一步提升逻辑推理及数学运算素养.
问题导学预习教材必备知识探究
内容索引
互动合作研析题型关键能力提升
拓展延伸分层精练核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1
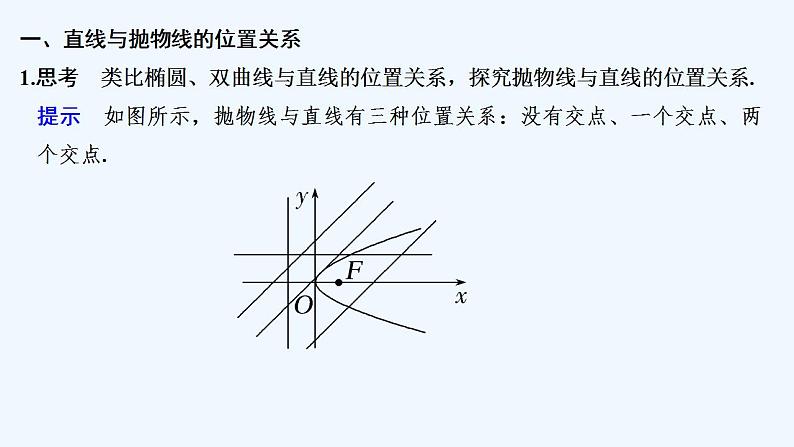
一、直线与抛物线的位置关系1.思考　类比椭圆、双曲线与直线的位置关系，探究抛物线与直线的位置关系.
提示　如图所示，抛物线与直线有三种位置关系：没有交点、一个交点、两个交点.
(1)当k≠0时，若Δ>0，则直线与抛物线有____个不同的公共点，此时直线与抛物线______；若Δ＝0，则直线与抛物线有____个公共点，此时直线与抛物线______；若Δ0)的内部，所以当k＝0时，直线与抛物线有一个公共点；当k≠0，直线与抛物线有两个公共点.故选C.
二、弦长问题1.思考　过抛物线y2＝2px(p>0)的焦点的直线交抛物线于A(x1，y1)，B(x2，y2)两点，那么线段AB叫作焦点弦，如图.如何求弦AB的长度？
提示　(1)利用弦长公式.
(2)根据抛物线的定义AB＝x1＋x2＋p.
2.填空　(1)一般弦长
x1＋x2＋p
温馨提醒　设过抛物线焦点的弦的端点为A(x1，y1)，B(x2，y2)，则四种标准方程形式下的弦长公式为：
3.做一做　过抛物线y2＝4x的焦点作直线交抛物线于A(x1，y1)，B(x2，y2)两点，若x1＋x2＝10，则弦AB的长度为(　　) A.16 B.14 C.12 D.10
C
解析　设抛物线的焦点为F(1，0)，则AB＝AF＋BF＝x1＋1＋x2＋1＝x1＋x2＋2＝10＋2＝12.
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
2
例1 已知直线l：y＝kx＋1，抛物线C：y2＝4x，当k为何值时，l与C：只有一个公共点；有两个公共点；没有公共点？
题型一　直线与抛物线的位置关系
①当Δ>0，即k0，则y1＋y2＝4m，y1y2＝－16，
8.已知A(2，0)，B为抛物线y2＝x上的一点，则AB的最小值为________.
11.(多选)已知抛物线y2＝2px(p>0)上三点A(x1，y1)，B(1，2)，C(x2，y2)，F为抛物线的焦点，则下列说法正确的是(　　 )
ABD
解析　把点B(1，2)代入抛物线方程y2＝2px，得p＝2，所以抛物线的准线方程为x＝－1，故A正确；
设AC的中点为M(x0，y0)，
因为AF＋CF≥AC，AF＋CF＝x1＋1＋x2＋1＝2x0＋2，所以2x0＋2≥6，得x0≥2，即AC的中点到y轴距离的最小值为2，故D正确.
(2)设直线l与C交于P，Q，若线段PQ的中点的纵坐标为1，求△OPQ的面积的最大值.
解　由题意知直线l的斜率存在，设直线l的方程为y＝kx＋b(b≥0)，代入抛物线方程，可得x2－4kx－4b＝0.设P(x1，y1)，Q(x2，y2)，则x1＋x2＝4k，x1x2＝－4b，所以y1＋y2＝4k2＋2b，因为线段PQ的中点的纵坐标为1，所以2k2＋b＝1，即2k2＝1－b≥0，所以0