









高中苏教版 (2019)5.3 导数在研究函数中的应用课文内容课件ppt
展开1.结合实例,借助几何直观了解函数的单调性与导数的关系.2.能利用导数研究函数的单调性.3.对于多项式函数,能求不超过三次的多项式函数的单调区间.
通过利用导数研究函数的单调性,结合函数的图象对其加以理解,发展学生的数学运算和直观想象素养.
问题导学预习教材必备知识探究
互动合作研析题型关键能力提升
拓展延伸分层精练核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1.思考 观察下面几个图象,探究函数的单调性和导数的正负的关系.
提示 (1)函数y=x的定义域为R,并且在定义域上是增函数,其导数y′=1>0;(2)函数y=x2的定义域为R,在(-∞,0)上为减函数,在(0,+∞)上为增函数,而y′=2x,当x<0时,其导数y′<0;当x>0时,其导数y′>0;当x=0时,其导数y′=0.
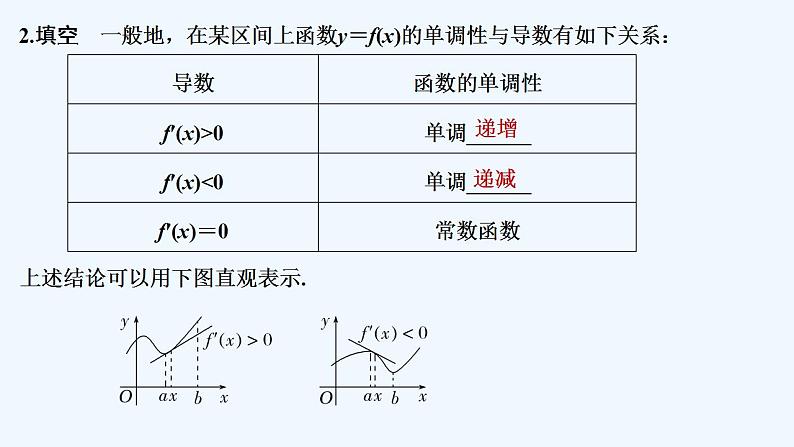
2.填空 一般地,在某区间上函数y=f(x)的单调性与导数有如下关系:
上述结论可以用下图直观表示.
温馨提醒 (1)一般地,可导函数y=f(x)在区间(a,b)内是增(减)函数的充要条件是:对任意的x∈(a,b),都有f′(x)≥0(f′(x)≤0),且f′(x)在(a,b)的任何子区间内都不恒等于0.(2)在某个区间内,若仅有有限个点所对应的导数值为0,则不能判定f(x)为常数函数.
3.做一做 函数f(x)=x+ln x在(0,6)上的单调性是( )
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
例1 (1)已知f(x)的导函数f′(x)的图象如图所示,那么f(x)的图象最有可能是图中的( )
题型一 函数图象与导函数图象的关系
解析 由题意可知,当x<0和x>2时,导函数f′(x)<0,函数f(x)是减函数;当x∈(0,2)时,导函数f′(x)>0,函数f(x)是增函数,故函数f(x)的图象如图D.
(2)已知函数f(x)与其导函数f′(x)的图象如图所示,则满足f′(x)
训练1 (多选)在同一坐标系中作出三次函数f(x)=ax3+bx2+cx+d(a≠0)及其导函数的图象,下列一定不正确的是( )
解析 当f′(x)>0时,y=f(x)是增加的;当f′(x)<0时,y=f(x)是减少的.故可得,A,B中函数图象的增减趋势与导函数的正负区间是吻合的;而C中导函数为负的区间内相应的函数不递减,故错误;D中导函数为负的区间内相应的函数不递减,故错误.
例2 (1)求证:函数f(x)=ex-x-1在(0,+∞)内是增函数,在(-∞,0)内是减函数;
题型二 判断(证明)函数的单调性
证明 由于f(x)=ex-x-1,所以f′(x)=ex-1,x∈R,当x∈(0,+∞)时,ex>1,即f′(x)=ex-1>0.故函数f(x)在(0,+∞)内为增函数,当x∈(-∞,0)时,ex<1,即f′(x)=ex-1<0.故函数f(x)在(-∞,0)内为减函数.
利用导数判断函数单调性的步骤:确定函数的定义域;求导数f′(x);确定f′(x)在定义域内的符号,在此过程中,需要对导函数进行通分、因式分解等变形;得出结论.
训练2 利用导数判断下列函数的单调性:
题型三 求函数的单调区间
例3 求下列函数的单调区间.
求函数y=f(x)的单调区间的步骤(1)确定函数y=f(x)的定义域.(2)求导数y′=f′(x).(3)解不等式f′(x)>0,函数在解集与定义域的交集上为增函数.(4)解不等式f′(x)<0,函数在解集与定义域的交集上为减函数.
训练3 求下列函数的单调区间: (1)f(x)=2x3+3x2-36x+1;
解 f(x)的定义域为R,f′(x)=6x2+6x-36.由f′(x)>0得6x2+6x-36>0,解得x<-3或x>2;由f′(x)<0解得 -3
3.注意1个易错点 讨论函数单调性时忽略定义域.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
1.函数f(x)=cs x-x在(0,π)上的单调性是( )A.先增后减 B.先减后增C.单调递增 D.单调递减
2.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则其导函数y=f′(x)的图象可能是( )
解析 由函数y=f(x)的图象,知当x<0时,f(x)单调递减;当x>0时,f(x)先递增,再递减,最后再递增,分析知y=f′(x)的图象可能为D.
3.(多选)如图是函数y=f(x)的导函数f′(x)的图象,则下列判断正确的是( )
A.在区间(-2,1)上,f(x)是增函数B.在(1,2)上,f(x)是增函数C.在(4,5)上,f(x)是增函数D.在(-3,-2)上,f(x)是增函数
解析 由题图知当x∈(1,2),x∈(4,5)时,f′(x)>0,所以在(1,2),(4,5)上,f(x)是增函数,当x∈(-3,-2)时,f′(x)<0,所以在(-3,-2)上,f(x)是减函数.
4.函数f(x)=ln x-4x+1的单调递增区间为( )
5.(多选)函数f(x)=xln x( )
6.函数y=x2-4x+a的单调递增区间为________,单调递减区间为________.
解析 函数的定义域为R,y′=2x-4,令y′>0,得x>2;令y′<0,得x<2,所以y=x2-4x+a的单调递增区间为(2,+∞),单调递减区间为(-∞,2).
8.函数f(x)=x2-5x+2ln(2x)的单调递增区间是__________________.
9.判断函数f(x)=2x(ex-1)-x2的单调性.
解 函数f(x)的定义域为R,f′(x)=2(ex-1+xex-x)=2(ex-1)(x+1).当x∈(-∞,-1)时,f′(x)>0;当x∈(-1,0)时,f′(x)<0;当x∈(0,+∞)时,f′(x)>0.故f(x)在(-∞,-1)和(0,+∞)上单调递增,在(-1,0)上单调递减.
(2)求函数f(x)的单调区间.
可知h(x)在(0,+∞)上为减函数,由h(1)=0知,当0
解析 由奇函数的定义可知,A,B,D均为奇函数,C为偶函数,所以排除C;对于选项A,y′=6x2+4>0,所以y=2x3+4x在(0,1)上单调递增;对于选项B,y′=1-cs x≥0,且y′不恒为0,所以y=x+sin(-x)在(0,1)上单调递增;对于选项D,y′=2xln 2+2-xln 2>0,所以y=2x-2-x在(0,1)上单调递增.故选ABD.
12.函数f(x)=xcs x的导函数f′(x)在区间[-π,π]上的图象大致是( )
解析 因为f(x)=xcs x,所以f′(x)=cs x-xsin x.因为f′(-x)=f′(x),所以f′(x)为偶函数,所以函数图象关于y轴对称,排除C;由f′(0)=1可排除D;而f′(1)=cs 1-sin 1<0,排除B.
14.(多选)若函数exf(x)(e=2.718 28……是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数中具有M性质的是( )
A.f(x)=2-x B.f(x)=x2+2C.f(x)=3-x D.f(x)=cs x
【最新版】高中数学(新苏教版)习题+同步课件午练18 导数与函数的单调性: 这是一份【最新版】高中数学(新苏教版)习题+同步课件午练18 导数与函数的单调性,文件包含午练18导数与函数的单调性pptx、午练18导数与函数的单调性doc等2份课件配套教学资源,其中PPT共14页, 欢迎下载使用。
数学选择性必修第一册5.3 导数在研究函数中的应用教案配套课件ppt: 这是一份数学选择性必修第一册5.3 导数在研究函数中的应用教案配套课件ppt,文件包含第二课时导数在实际中的应用pptx、第二课时导数在实际中的应用doc等2份课件配套教学资源,其中PPT共54页, 欢迎下载使用。
苏教版 (2019)选择性必修第一册5.3 导数在研究函数中的应用备课课件ppt: 这是一份苏教版 (2019)选择性必修第一册5.3 导数在研究函数中的应用备课课件ppt,文件包含第二课时导数与函数的单调性二pptx、第二课时导数与函数的单调性二doc等2份课件配套教学资源,其中PPT共49页, 欢迎下载使用。













