【最新版】高中数学（新苏教版）习题+同步课件培优课　利用导数研究恒成立、能成立问题

这是一份【最新版】高中数学（新苏教版）习题+同步课件培优课　利用导数研究恒成立、能成立问题，文件包含培优课利用导数研究恒成立能成立问题pptx、培优课利用导数研究恒成立能成立问题doc等2份课件配套教学资源，其中PPT共10页， 欢迎下载使用。
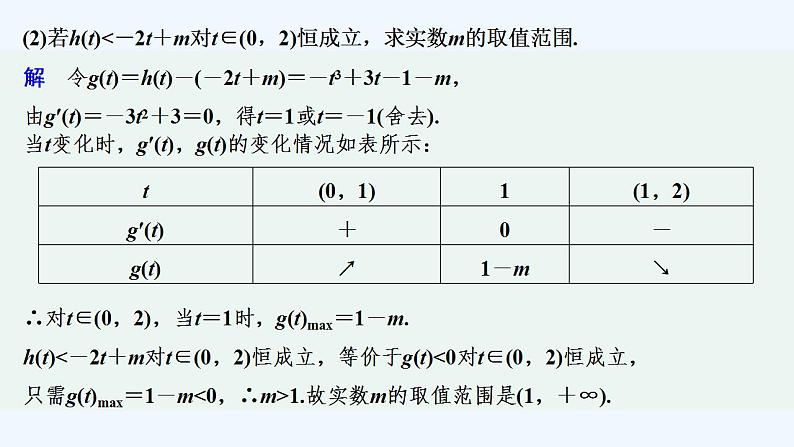
培优课　利用导数研究恒成立、能成立问题恒(能)成立问题的转化策略：若f(x)在区间D上有最值，则(1)恒成立：∀x∈D，f(x)>0⇔f(x)min>0；∀x∈D，f(x)<0⇔f(x)max<0.(2)能成立：∃x∈D，f(x)>0⇔f(x)max>0；∃x∈D，f(x)<0⇔f(x)min<0.恒成立与能成立问题，要注意理解“任意”与“存在”的不同含义，要注意区分转化成的最值问题的异同.类型一　不等式恒成立求参数的值(取值范围)例1 设函数f(x)＝tx2＋2t2x＋t－1(x∈R，t>0).(1)求f(x)的最小值h(t)；(2)若h(t)<－2t＋m对t∈(0，2)恒成立，求实数m的取值范围.解　(1)∵f(x)＝t(x＋t)2－t3＋t－1(x∈R，t>0)，∴当x＝－t时，f(x)取最小值f(－t)＝－t3＋t－1，即h(t)＝－t3＋t－1.(2)令g(t)＝h(t)－(－2t＋m)＝－t3＋3t－1－m，由g′(t)＝－3t2＋3＝0，得t＝1或t＝－1(舍去).当t变化时，g′(t)，g(t)的变化情况如表所示：t(0，1)1(1，2)g′(t)＋0－g(t)↗1－m↘∴对t∈(0，2)，当t＝1时，g(t)max＝1－m.h(t)<－2t＋m对t∈(0，2)恒成立，等价于g(t)<0对t∈(0，2)恒成立，只需g(t)max＝1－m<0，∴m>1.故实数m的取值范围是(1，＋∞).思维升华　(1)“恒成立”问题向最值问题转化是一种常见的题型，一般地，可采用分离参数法进行转化，λ≥f(x)恒成立⇔λ≥f(x)max；λ≤f(x)恒成立⇔λ≤f(x)min，对于不能分离参数的恒成立问题，直接求含参函数的最值即可.(2)此类问题特别要小心“最值能否取得到”和“不等式中是否含等号”的情况，以此来确定参数的范围能否取得“＝”.类型二　不等式能成立求参数的值(取值  范围)例2 已知函数f(x)＝x2－(2a＋1)x＋aln x(a∈R).(1)若f(x)在区间[1，2]上是单调函数，求实数a的取值范围；(2)函数g(x)＝(1－a)x，若∃x0∈[1，e]使得f(x0)≥g(x0)成立，求实数a的取值范围.解　(1)f′(x)＝，当导函数f′(x)的零点x＝a落在区间(1，2)内时，函数f(x)在区间[1，2]上就不是单调函数，即a∉(1，2)，所以实数a的取值范围是(－∞，1]∪[2，＋∞).(2)由题意知，不等式f(x)≥g(x)在区间[1，e]上有解，即x2－2x＋a(ln x－x)≥0在区间[1，e]上有解.因为当x∈[1，e]时，ln x≤1≤x(不同时取等号)，所以x－ln x>0，所以a≤在区间[1，e]上有解.令h(x)＝，则h′(x)＝.因为x∈[1，e]，所以x＋2>2≥2ln x，所以h′(x)≥0，h(x)在[1，e]上单调递增，所以x∈[1，e]时，h(x)max＝h(e)＝，所以a≤，所以实数a的取值范围是.思维升华　1.含参数的能成立(存在型)问题的解题方法若a≥f(x)在x∈D上能成立，则a≥f(x)min；若a≤f(x)在x∈D上能成立，则a≤f(x)max.2.含全称、存在量词不等式能成立问题(1)若存在x1∈A，对任意x2∈B，使f(x1)≥g(x2)成立，则f(x)max≥g(x)max；(2)若对任意x1∈A，存在x2∈B，使f(x1)≥g(x2)成立，则f(x)min≥g(x)min.