





沪科版八年级下册20.2 数据的集中趋势与离散程度课堂教学ppt课件
展开1.掌握平均数和加权平均数的概念,会求一组数据的平均数和加权平均数.(重点)2.会用平均数和加权平均数解决实际生活中的问题.(难点)
1.数据1、2、3、4、5的平均数是 .
2.一次数学测验,3名同学的数学成绩分别是60,80和100分,则他们的平均成绩是多少?你怎样列式计算?算式中的分子分母分别表示什么含义?
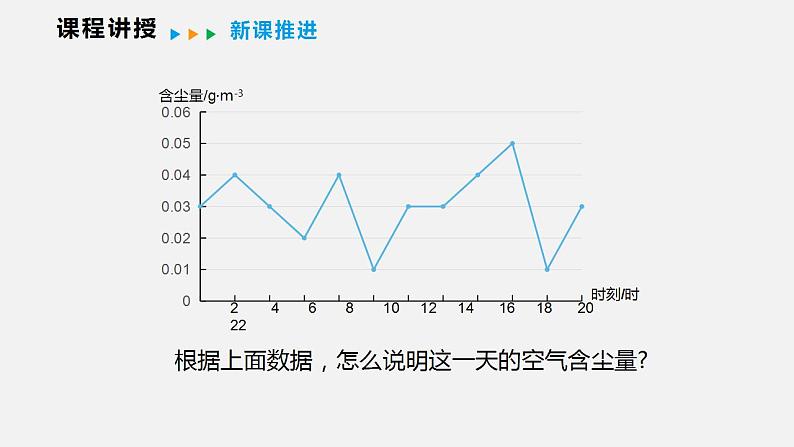
问题1 某校“环保宣传”小组定期对学校的空气含尘量进行检测,下面是某天每隔2h测得的数据:
0.03,0.04,0.03,0.02,0.04,,0.03,0.04,0.05,0.01,0.03
2 4 6 8 10 12 14 16 18 20 22
根据上面数据,怎么说明这一天的空气含尘量?
解:计算上述数据的平均数:
把这个平均数作为这组数据的一个代表,用来反映该日空气含尘量的一般状况,我们说学校这一天的空气含尘量平均为0.03(g/m-3)
日常生活中,我们常用平均数表示一组数据的“平均水平”. 一般地,如果有 n 个数据
x1,x2,…,xn,
对于一组数据,我们常用平均数来作为刻画它的集中趋势的一种方法;平均数是反映数据的平均水平的一个特征量.
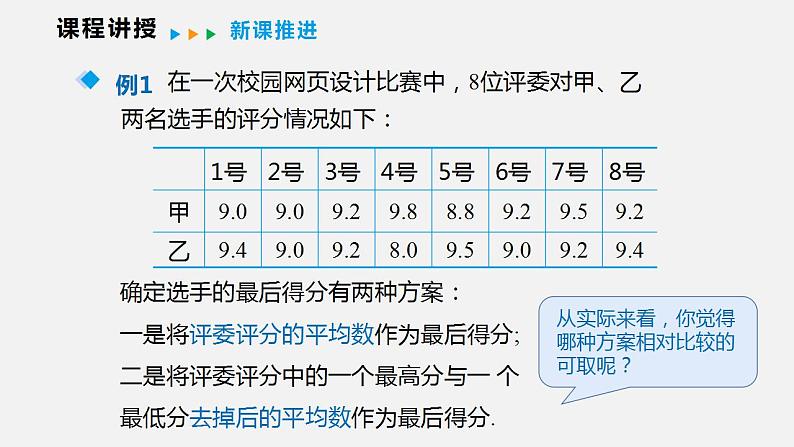
在一次校园网页设计比赛中,8位评委对甲、乙两名选手的评分情况如下:
确定选手的最后得分有两种方案:一是将评委评分的平均数作为最后得分; 二是将评委评分中的一个最高分与一 个最低分去掉后的平均数作为最后得分.
将上面的得分与表中的数据相比较,我们发现有5位评委对甲的评分不高于乙,这表明多数人认为乙的成绩比较好.方案二的结果表明乙的成绩比甲的高,与大多数评委的观点相符.因此,方案二评定选手的最后得分比较可取.
个体户张某经营一家餐馆,下面是该餐馆所有工作人员200年10月份的工资:
张某: 4000元; 会计: 700元; 厨师甲:1000元
厨师乙: 900元; 杂工甲:580元; 杂工乙:560元
服务员甲:620元;服务员乙:600元;服务员丙:580元
(1) 计算他们的平均工资,这个平均工资能否反映餐馆加工在这个月收入的一般水平?
(2) 不计张某的工资,再求餐馆员工的月平均工资,这个平均工资能代表一般水平吗?
用平均数作为一组数据的代表,容易受到个别极端数值的影响.
想一想怎样避免这个缺点?
为了消除这种现象,可将少数极端数据去掉,只计算余下的数据的平均数,并把所得的结果作为全部数据的平均数.如某些评奖比赛的计分,通常去掉一个最高分和一个最低分.
(1) 如果学校将教学设计、课堂教学和答辩按1:3:1的比例来计算各人的考评成绩,那么谁会被录用?
(2)如果按教学设计占30%、课堂教学占50%、答辩占20%来计算各人的成绩,那么谁会被录用?
乙的考评成绩为 80×30%+92×50%+83×20%=86.6(分)
(2)甲的考评成绩为 90×30%+85×50%+90×20%=87.5 (分)
上例中是用什么来表示各个指标的重要程度?
(1)是用各项所占比例的形式来表示各个指标的重要程度的.
(2)是用各项所占百分比的形式来表示各个指标的重要程度的.
它们都是用来衡量各项考评成绩在总评分中所占权重”,“权重”不一样,结果就不一样.
一般地,对上面的求平均数,可统一用下面的公式
通过例2,我们可以看出数据的权能反映数据的相对“重要程度”.
公式②和公式①有什么关系?
公式①是公式②的一种特殊形式,即当 f1=1,f2=1,f3=1,…,fk=1时,公式②就是公式①.
2、若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是( )
1、某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( ) A.84 B. 86 C. 88 D. 90
求一组数据的平均数,当数据很多时,用笔算比较麻烦,这是用计算器就很方面。只要按着指定的方法将各个数据依次输入计算器,即可直接得出结果。下面我们以例1中求选手甲的平均数为例加以说明.
已知:x1,x2,x3,…, x10的平均数是a,x11,x12,x13,… ,x30的平均数是b,则x1,x2,x3,… ,x30的平均数( )
A.(a+b)
若x1,x2,x3,···,xn的平均数为 ,则
(1) nx1,nx2,nx3,···,nxn的平均数为 .
(2) x1+b,x2+b,x3+b,···,xn+b的平均数为 .
(3) nx1+b,nx2+b,nx3+b,···,nxn+b的平均数为 .
拓展练习 若x1,x2,…, xn 的平均数为 ,y1,y2,…, yn 的平均数为 ,则 x1+y1,x2+y2,x3+y3,···,xn+yn 的平均数为 .
一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下
如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
85×3+83×3+78×2+75×2 3+3+2+2
73×3+80×3+85×2+82×2 3+3+2+2
显然甲的成绩比乙的高,所以从成绩看,应该录取甲.
听、说、读、写的成绩按照3:3:2:2的比确定.
数学八年级下册20.2 数据的集中趋势与离散程度评课课件ppt: 这是一份数学八年级下册20.2 数据的集中趋势与离散程度评课课件ppt,共12页。PPT课件主要包含了跟踪练习,评分表,哪一种方案更为可取,练一练等内容,欢迎下载使用。
数学沪科版20.2 数据的集中趋势与离散程度优质ppt课件: 这是一份数学沪科版20.2 数据的集中趋势与离散程度优质ppt课件,共29页。PPT课件主要包含了观察与思考,平均数,合作探究,想一想,归纳总结,典例精析,练一练,加权平均数,B的平均成绩为,C的平均成绩为等内容,欢迎下载使用。
初中数学沪科版八年级下册第20章 数据的初步分析20.2 数据的集中趋势与离散程度集体备课ppt课件: 这是一份初中数学沪科版八年级下册第20章 数据的初步分析20.2 数据的集中趋势与离散程度集体备课ppt课件,共18页。PPT课件主要包含了学习目标及重难点,课程导入,课程讲授,新课推进,习题解析,习题1,习题2,习题3,2如图所示等内容,欢迎下载使用。













