初中数学北师大版八年级上册2 平方根备课ppt课件

这是一份初中数学北师大版八年级上册2 平方根备课ppt课件，共20页。PPT课件主要包含了学习目标，情境导入，探索交流，x2+1，y2+1，z2+1，例题解析，7因为，练习巩固等内容，欢迎下载使用。

1.了解算术平方根的概念及其性质．（重点）2.会求一个数的算术平方根.（难点）
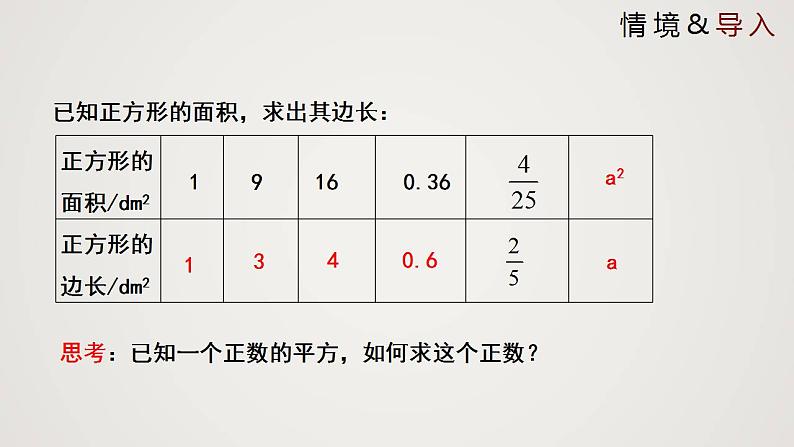
已知正方形的面积，求出其边长：
思考：已知一个正数的平方，如何求这个正数？
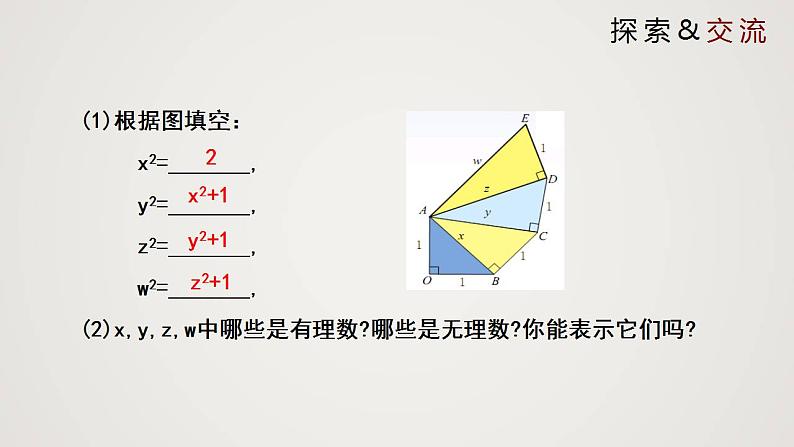
(1)根据图填空： x2=_______, y2=_______, z2=_______, w2=_______,(2)x,y,z,w中哪些是有理数?哪些是无理数?你能表示它们吗?
因为没有任何整数或分数的平方等于2，3，5，所以x、y、w不是有理数，而是无理数，因为22=4.所以z=2，是有理数.
定义：一般地，如果一个正数x的平方等于a，即x2＝a，那么这个正数x就叫做a的算术平方根．规定：0的算术平方根是0.表示方法：正数a的算术平方根表示为 读作 “根号a”．
算术平方根等于自身的数是0和1.
特别提醒正数的算术平方根是一个正数，0的算术平方根是0（ =0），负数没有算术平方根.
例1.下列说法中,正确的是(　　)A．3是9的算术平方根　　　　　　 B．-2是4的算术平方根C.(-2)2的算术平方根是-2 D．-9的算术平方根是3
例2.求下列各数的算术平方根： (1)900; (2)1; (3) ； (4) 14.
例3.求下列各数的算术平方根：(1)64； (2) (3)0.36； (4) 52； (5) (-5)2；(6)0； (7) (8)7； (9) -16.
解：(1) 因为82＝64 ，所以64的算术平方根是8，即 (2) 因为 所以 的算术平方根是 ， (3) 因为0.62＝0.36，所以0.36的算术平方根是0.6，即(4) 因为 52=52，所以52的算术平方根是5，
(5) 因为52＝（-5）2 ，所以 （-5）2的算术平方根是5， (6) 0算术平方根是 0 . ，9的算术平方根是3，所以 的算术平方根是3.(8) 7的算术平方根是
要点精析1.求带分数的算术平方根，先将带分数化成假分数，再求算术平方根.2.求一个数的算术平方根必须明确两点：（1）这个数是非负数；（2）求出的算术平方根（结果）必须是非负数.
思考：(1)-4有算术平方根吗？即有一个正数的平方等于-4吗？(2)什么数才有算术平方根？
负数没有算术平方根；非负数才有算术平方根
(1)正数有一个正的算术平方根;(2)0的算术平方根是0;(3)负数没有算术平方根;
1.要点精析：(1)算术平方根 具有双重非负性：①a是非负数，即a ≥0；②算术平方根 是非负数，即 ≥0.(2)算术平方根是它本身的数只有0和1.
2.性质：(1)算术平方根是一个非负数 ，即 (2)在 中，a称为被开方数，也是非负数，即a ≥0.我们可 以说 具有“双重非负性”，即
例4.自由下落物体的高度h（米）与下落时间t（秒）的关系为h=4.9 t2．有一铁球从19.6米高的建筑物上自由下落，到达地面需要多长时间？
解:将h=19.6代入公式 h=4.9 t2,得 t2 =4,所以t =2(秒).即铁球到达地面需要2秒.
1.16的算术平方根是（　　）A. 2B. 4C. ±2D. ±4
2.下列说法正确的是（　　）A. 5是25的算术平方根 B. -6是36的算术平方根C. 0的算术平方根是0 D. 0.01是0.1的算术平方根
3.在Rt△ABC中，∠C=90°，BC=3，AC=5.求AB的长.
4.(1)已知y＝ ＋ ＋5，求2x的算术平方根．
(2)已知x，y为有理数，且 ＋3(y－2)2＝0，求x－y的值．