高中数学人教A版 (2019)必修 第一册第五章 三角函数5.2 三角函数的概念精品ppt课件

课题名

5.2.1三角函数的概念第2课时

教学目标

1.掌握任意角三角函数(正弦、余弦、正切)在各象限的符号；

2.掌握公式一并会应用。

教学重点

掌握任意角三角函数(正弦、余弦、正切)在各象限的符号

教学难点

掌握公式一并会应用

教学准备

教师准备：幻灯片、黑板、投影

学生准备：笔、纸、课本

教学过程

一、 新课引入

【探究1】根据三角函数的定义,各个三角函数值是用单位圆上点的坐标表示的,当角在不同象限时,其与单位圆的交点坐标的符号就不同,因此其各个三角函数值的正负就不同,你能推导出sin α,cos α,tan α在不同象限内的符号吗?

【提示】根据各个象限点的坐标的符号去探究。

当α在第一象限时,sin α>0, cos α>0, tan α>0;

当α在第二象限时,sin α>0, cos α<0, tan α<0;

当α在第三象限时,sin α<0, cos α<0, tan α>0;

当α在第四象限时,sin α<0, cos α>0, tan α<0.

【探究2】30°,390°,-330°三个角的终边有什么关系?它们与单位圆的交点坐标相同吗?这三个角的正弦值、余弦值、正切值相等吗?

【提示】终边相同,所以角的终边与单位圆的交点坐标相同,三个角的正弦值、余弦值、正切值相等.

【设计意图】

通过复习任意角的三角函数的定义，引入本节新课，建立知识间的联系，提高学生概括推理的能力。

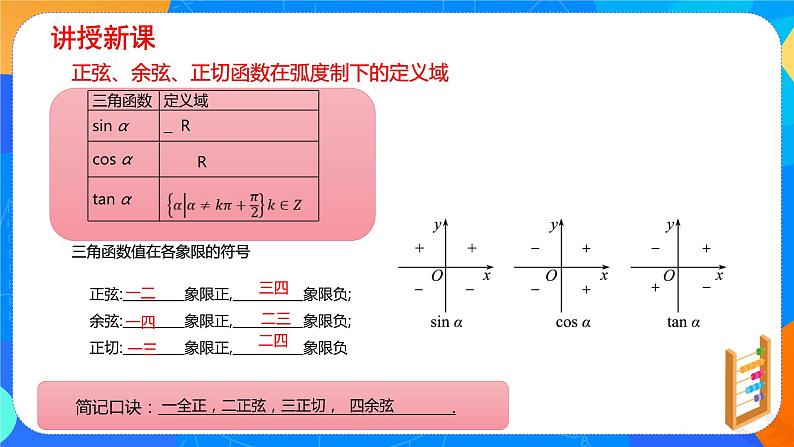
二、讲授新课

正弦、余弦、正切函数在弧度制下的定义域

三角函数值在各象限的符号：

正弦:一二象限正,三四象限负;

余弦:一四象限正,二三象限负;

正切:一三象限正,二四象限负.

简记口诀：一全正，二正弦，三正切，四余弦。

【思考1】若sin α>0,则α的终边落在第一象限或第二象限内？

【提示】若sin α>0,则α的终边不一定落在第一象限或第二象限内,有可能终边落在y轴的非负半轴上.

【做一做1】sin 145°     0， cos(-210°)      0， tan 405°      0.

【做一做2】判断正误(正确的打“√”，错误的打“×”)

(1)已知α是三角形的内角，则必有sinα>0.(　　)

(2)任意角α的正弦值sinα、余弦值cosα、正切值tanα都有意义．(　　)

【设计意图】

通过探究让学生理解判断任意角的三角函数值的正负，提高学生解决问题的能力。

【探究1】终边相同的角的同名三角函数值相等吗?

【提示】相等.由三角函数的定义可知,终边相同的角的三角函数值相等.

【探究2】若sin α=sin β,则一定有α=β吗?

【提示】不一定.由终边相同的角的表示可知,当α与β的终边相同时,它们的正弦值虽然相等,但这两个角不一定相等.

【探究3】　同一三角函数值相等时，角是否一定相等或相差周角的整数倍？

【提示】不一定，如sin 30°＝sin 150°＝.

公式一：

（1）       语言表示:终边相同的角的同一三角函数的值相等．

（2）式子表示：

sin(α＋k·2π)＝sinα，

cos(α＋k·2π)＝cosα，

tan(α＋k·2π)＝tanα，其中k∈Z.

(1)公式一的实质：是说终边相同的角的三角函数值相

等，即角α的终边每绕原点旋转一周，函数值将重复出现一次，体现了三角函数特有的“周而复始”的变化规律．

(2)公式一的作用

利用诱导公式一可把负角的三角函数化为0～2π间角的三角函数，亦可把大于2π的角的三角函数化为0～2π间角的三角函数，即实现了“负化正，大化小”.

【做一做1】判断正误(正确的打“√”，错误的打“×”)

(1)若α＝β＋720°，则cosα＝cosβ.(　　)

(2)若sinα＝sinβ，则α＝β.(　　)

【做一做2】tan765°=     ；cos 405°=      ；sin =     .

【答案】1； ；

例1. 确定下列式子的符号：

(1) tan 108°·cos 305°；(2)；(3)tan 120°·sin 269°.

【解析】(1)∵108°是第二象限角，∴tan 108°＜0.

∵305°是第四象限角，∴cos 305°＞0.从而tan 108°·cos 305°＜0.

(2)∵是第二象限角，是第四象限角，是第二象限角

∴cos ＜0，tan＜0，sin ＞0.从而

∴sin 269°＜0.从而tan 120°sin 269°＞0.

【类题通法】判断三角函数值在各象限符号的攻略

(1)基础：准确确定三角函数值中各角所在象限；

(2)关键：准确记忆三角函数在各象限的符号；

(3)注意：用弧度制给出的角常常不写单位，不要误认为角度导致象限判断错误．

提醒：注意巧用口诀记忆三角函数值在各象限符号．

【巩固练习1】

(1)若α是第四象限角，则点P(cos α，tan α)在第________象限．

(2)判断下列各式的符号：①sin 183°；②tan ；③cos 5.

【解析】(1)∵α是第四象限角，∴cos α>0，tan α<0，

∴点P(cos α，tan α)在第四象限．

(2)　①∵180°<183°<270°，在第三象限，∴sin 183°<0；

②∵<<2π，在第四象限，∴tan <0；③∵<5<2π，在第四象限∴cos 5>0.

例2. 求值：(1)tan 405°－sin 450°＋cos 750°；

(2)sincos＋tancos.

【解析】　(1)原式＝tan(360°＋45°)－sin(360°＋90°)＋cos(2×360°＋30°)

＝tan 45°－sin 90°＋cos 30°＝1－1＋＝.

(2)原式＝sincos＋tan·cos

＝sincos＋tancos＝×＋1×＝.

【类题通法】利用诱导公式一进行化简求值的步骤

(1)定形：将已知的任意角写成2kπ＋α的形式，其中α∈[0，2π)，k∈Z.

(2)转化：根据诱导公式，转化为求角α的某个三角函数值．

(3)求值：若角为特殊角，可直接求出该角的三角函数值．

【巩固练习2】

化简下列各式：

(1)a2sin(－1 350°)＋b2tan 405°－2abcos(－1 080°)；

(2)sin＋cosπ·tan 4π.

【解析】(1)原式＝a2sin(－4×360°＋90°)＋b2tan(360°＋45°)

－2abcos(－3×360°)

＝a2sin 90°＋b2tan 45°－2abcos 0°

＝a2＋b2－2ab＝(a－b)2.

(2)sin＋cosπ·tan 4π

＝sin＋cosπ·tan 0＝sin＋0＝.

三、课堂小结

四、达标检测

1．若α是第二象限角，则点P(sin α，cos α)在(　D　)

A．第一象限  B．第二象限

C．第三象限  D．第四象限

2.若sin θ cos θ>0，则θ在(　B　)

A．第一、二象限  B．第一、三象限

C．第一、四象限  D．第二、四象限

3.若点P坐标为(cos 2 014°，sin 2 014°)，则点P在(　C  　)

A．第一象限  B．第二象限

C．第三象限  D．第四象限

4.sinπ的值为________．

【设计意图】通过练习巩固本节所学知识，通过学生解决问题的能力，感悟其中蕴含的数学思想，增强学生的应用意识。

布置作业

完成对应的课后练习

板书设计

教学反思

学生基本上都掌握了本次课程内容，不过学生在角的范围这里还是会忘记属于整数的要求。