北师大版九年级上册4 探索三角形相似的条件课文配套课件ppt

这是一份北师大版九年级上册4 探索三角形相似的条件课文配套课件ppt，文件包含442《利用两边及夹角判定三角形相似》课件PPTpptx、442《利用两边及夹角判定三角形相似》教案docx等2份课件配套教学资源，其中PPT共16页， 欢迎下载使用。
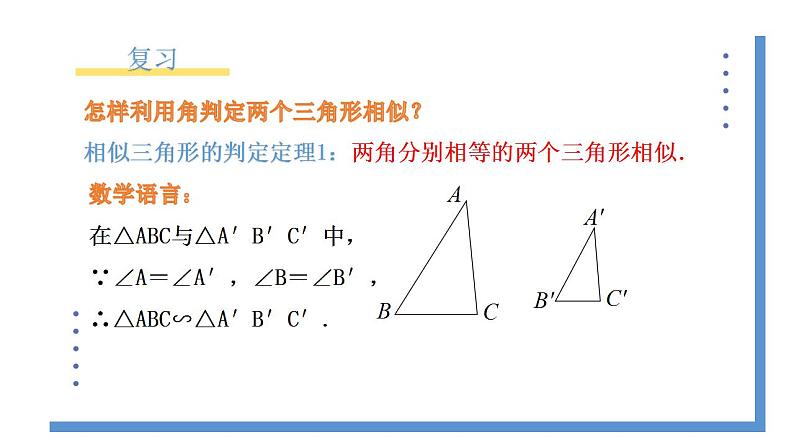
相似三角形的判定定理1：两角分别相等的两个三角形相似．
数学语言：在△ABC与△A′B′C′中，∵∠A＝∠A′，∠B＝∠B′，∴△ABC∽△A′B′C′.
怎样利用角判定两个三角形相似？
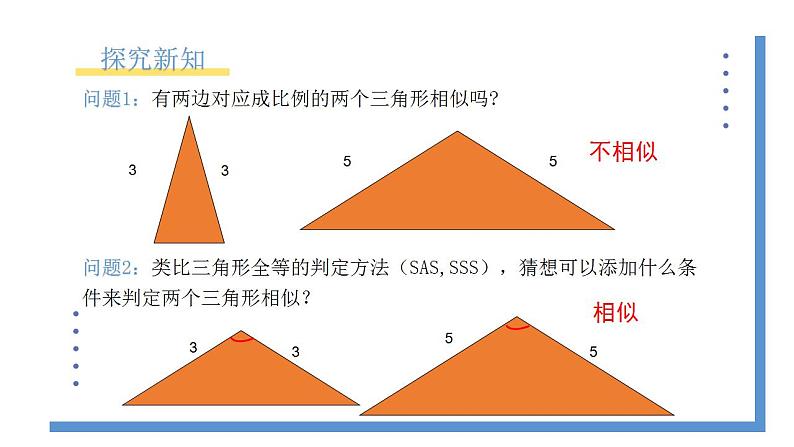
问题1：有两边对应成比例的两个三角形相似吗?
问题2：类比三角形全等的判定方法（SAS,SSS），猜想可以添加什么条件来判定两个三角形相似？
改变 k 和∠A 的值的大小，是否有同样的结论？
由此得到利用两边和夹角来判定三角形相似的定理：两边成比例且夹角相等的两个三角形相似．
∴ △ABC ∽ △A′B′C′ .
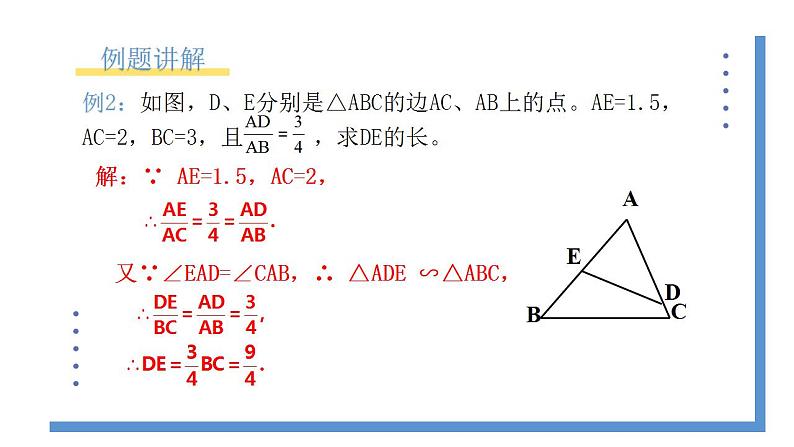
又∵∠EAD=∠CAB，∴ △ADE ∽△ABC，
解：∵ AE=1.5，AC=2，
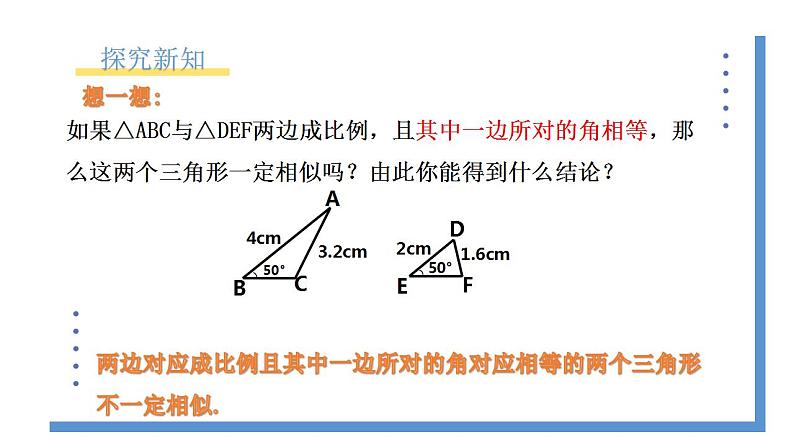
如果△ABC与△DEF两边成比例，且其中一边所对的角相等，那么这两个三角形一定相似吗？由此你能得到什么结论？
两边对应成比例且其中一边所对的角对应相等的两个三角形不一定相似.
如果两个三角形两边对应成比例，但相等的角不是两条对应边的夹角，那么两个三角形不一定相似，相等的角一定要是两条对应边的夹角.
(1) 两个等边三角形相似 ( )(2) 两个直角三角形相似 ( )(3) 两个等腰直角三角形相似( )(4) 有一个角是50°的两个等腰三角形相似( )
2.如图，在△ABC中，∠A＝78°，AB＝4，AC＝6.将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是(　　)
3.如图，D 是 △ABC 一边 BC 上一点，连接 AD，使 △ABC ∽ △DBA的条件是( )A. AC : BC=AD : BD B. AC : BC=AB : ADC. AB2 = CD · BCD. AB2 = BD · BC
4.如图，在直角坐标系中有两点A(4，0)，B(0，2)，如果点C在x轴上(C与A不重合)，当点C的坐标为_____________时，使得由点B、O、C组成的三角形与△AOB相似(不包括全等)．
(-1,0)或(1，0)
1.三角形相似的判定定理2：两边成比例且夹角相等的两个三角形相似.
2.两边对应成比例且其中一边所对的角对应相等的两个三角形不一定相似.