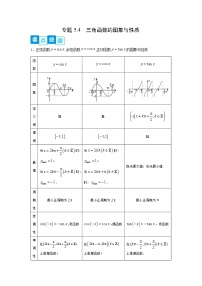
人教A版 (2019)必修 第一册第五章 三角函数5.4 三角函数的图象与性质精品同步练习题
展开专题5.4 三角函数的图象与性质
1.正弦函数,余弦函数,正切函数的图象与性质
函数 | |||
图象 | |||
定义域 | |||
值域 | |||
最值 | 当时,; 当时,. | 当时,; 当时,. | 既无最大值,也无最小值 |
周期性 | 最小正周期为 | 最小正周期为 | 最小正周期为 |
奇偶性 | ,奇函数 | ,偶函数 | ,奇函数 |
单调性 | 在上是增函数; 在上是减函数. | 在上是增函数; 在上是减函数. | 在上是增函数. |
对称性 | 对称中心; 对称轴, 既是中心对称图形又是轴对称图形. | 对称中心; 对称轴, 既是中心对称图形又是轴对称图形. | 对称中心; 无对称轴, 是中心对称图形但不是轴对称图形. |
2.函数的图象的画法
(1)变换作图法
由函数的图象通过变换得到(A>0,ω>0)的图象,有两种主要途径:“先平移后伸缩”与“先伸缩后平移”.如下图.
(2)五点作图法
找五个关键点,分别为使y取得最小值、最大值的点和曲线与x轴的交点.其步骤为:
①先确定最小正周期T=,在一个周期内作出图象;
②令,令X分别取0,,,,求出对应的x值,列表如下:
由此可得五个关键点;
③描点画图,再利用函数的周期性把所得简图向左右分别扩展,从而得到的简图.
3.函数(A>0,ω>0)的性质
(1)奇偶性:时,函数为奇函数;
时,函数为偶函数.
(2)周期性:存在周期性,其最小正周期为T= .
(3)单调性:根据y=sint和t=的单调性来研究,
由得单调增区间;
由得单调减区间.
(4)对称性:利用y=sin x的对称中心为求解,
令,求得x.
利用y=sin x的对称轴为求解,
令,得其对称轴.
一、单选题
1.函数在上的递增区间为
A. B.
C. D.
2.已知在区间上的最大值为,则
A. B.
C. D.
3.函数的一个对称中心的坐标是
A. B.
C. D.
4.已知函数,则的最大值为
A. B.3
C.4 D.5
5.函数最小正周期为
A. B.
C. D.
6.已知函数,则
A.的最小正周期为,对称中心为
B.的最小正周期为,对称中心为
C.的最小正周期为,对称中心为
D.的最小正周期为,对称中心为
7.函数在区间上是增函数,在区间上是减函数,则的最小值为
A. B.
C.2 D.3
8.已知的最小正周期为,则
A. B.
C. D.
9.函数的一个对称中心是
A.(0,0) B.(,0)
C.(,0) D.以上选项都不对
10.若,,则“”是“”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
11.在①,②,③,④中,最小正周期为的所有函数为
A.①②③ B.②③④
C.②③ D.①③
12.函数y=2cos(2x+),x[-,]的值域是
A. B.
C. D.
13.函数的部分图象如图所示,则的解析式为
A. B.
C. D.
14.若,,则“”是“”的
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
15.下列函数中是奇函数,且最小正周期为π的函数是
A.y=tan2x B.y=|sinx|
C.y=cos2x D.y=sin2x
16.下列区间中是函数的单调递减区间的是
A. B.
C. D.
17.下列区间是函数的单调递减区间的是
A. B.
C. D.
18.已知在内有零点,且在上单调递减,则的取值范围是
A. B.
C. D.
19.的
A.最大值为4,最小正周期为 B.最大值为4,最小正周期为
C.最小值为0,最小正周期为 D.最小值为0,最小正周期为
20.若,则函数的零点为
A. B.
C. D.
21.已知函数的部分图象如图所示,且在上恰有一个最大值和一个最小值,则的取值范围是
A. B.
C. D.
22.已知,对任意,都存在使得成立,则下列取值可能的是
A. B.
C. D.
23.对于函数,下列结论正确的是
A.是以为周期的函数
B.的减区间为
C.的最大值为1
D.图象的对称轴为
24.函数(,)在区间上不可能
A.单调递增 B.单调递减
C.有最大值 D.有最小值
25.已知,若存在使得集合中恰有3个元素,则的取值不可能是
A. B.
C. D.
二、多选题
1.下列函数中,同时满足:①在上是增函数;②为奇函数;③周期为的函数有
A. B.
C. D.
2.如图是函数的部分图象,则下列说法正确的是
A. B.是函数的一个对称中心
C. D.函数在区间上是减函数
3.已知函数,则下列结论错误的是
A.是偶函数 B.是增函数
C.是周期函数 D.的值域为
4.对于函数,下列说法正确的是
A.最小正周期为 B.对称轴方程为
C.其图象关于点对称 D.单调增区间是
5.已知某物体作简谐运动,位移函数为,且,则下列说法正确的是
A.该简谐运动的初相为
B.函数在区间上单调递增
C.若,则
D.若对于任意,,都有,则
三、填空题
1.已知函数,则的对称中心为___________.
2.函数的最小正周期为,则___________.
3.函数,的值域是___________.
4.函数的值域是___________.
5.函数的单调递增区间是______.
6.用“五点法”作函数,的大致图象,所取的五点是___________.
7.已知函数,则的对称中心为___________.
8.已知函数(,,)的部分图象如图,则函数的解析式为___________.
9.设,则函数的最小值为___________.
10.若已知,函数在上单调递增,则的取值范围是___________.
11.设,,,则a,b,c的大小关系为___________.
12.设函数,则___________.
13.已知函数,若关于x的方程在上有两个不同的解,则实数m的取值范围是___________.
14.与的大小关系是___________.
15.函数的单调递增区间是___________.
16.若函数,的最小正周期为,且,则的取值范围是______.
17.已知函数,,则该函数的图象最高点的纵坐标是______.
18.已知函数与函数的图象关于原点对称,则函数的解析式为___________.
19.已知函数.给出下列四个结论:
①的最小正周期为.
②在区间上单调递减.
③的最大值为1.
④当时,取得极值.
以上正确结论的序号是___________.(写出所有正确的序号)
20.已知函数()的一个零点是,则的单调减区间是___________.
21.函数的单调递增区间是___________.
22.函数,的值域是___________.
23.已知函数,的值域为,则实数的取值范围为___________.
24.设定义在上的函数,给出以下四个说法:
①的周期为;
②在区间上是增函数;
③的图象关于点对称;
④的图象关于直线对称.
以其中两个说法作为条件,另两个说法作为结论,写出一组你认为正确的一个命题(写成“”的形式)___________.(其中用到的说法用序号表示)
25.若不等式对任意的恒成立,则实数a的取值范围为___________.
四、解答题
1.已知函数.
(1)求的最小正周期;
(2)求的单调递增区间.
2.求下列函数的值域:
(1);
(2);
(3).
3.画出,的大致图象,并分别写出使和的取值范围.
4.已知函数,其中,,且,.
(1)求的解析式;
(2)求单调递增区间及对称轴;
(3)求.
5.已知函数的一条对称轴为直线.
(1)求;
(2)求的单调递增区间.
人教A版 (2019)必修 第一册5.4 三角函数的图象与性质课后练习题: 这是一份人教A版 (2019)必修 第一册5.4 三角函数的图象与性质课后练习题,文件包含专题54三角函数图像与性质解析版docx、专题54三角函数图像与性质原卷版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
人教A版 (2019)必修 第一册5.4 三角函数的图象与性质同步达标检测题: 这是一份人教A版 (2019)必修 第一册5.4 三角函数的图象与性质同步达标检测题,文件包含专题54三角函数的图象与性质解析版docx、专题54三角函数的图象与性质原卷版docx等2份试卷配套教学资源,其中试卷共46页, 欢迎下载使用。
专题5.4 三角函数的图象与性质- 2022-2023学年高一数学阶段性复习精选精练(人教A版2019必修第一册): 这是一份专题5.4 三角函数的图象与性质- 2022-2023学年高一数学阶段性复习精选精练(人教A版2019必修第一册),文件包含专题54三角函数图像与性质解析版docx、专题54三角函数图像与性质原卷版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。