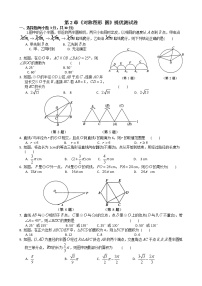
苏科版九年级上册第2章 对称图形——圆综合与测试同步训练题

这是一份苏科版九年级上册第2章 对称图形——圆综合与测试同步训练题，共43页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
第2章《对称图形--圆》单元复习培优卷

一、选择题
1、已知⊙O的直径为10，点P到点O的距离大于8，那么点P的位置（ ）
A．一定在⊙O的内部 B．一定在⊙O的外部 C．一定在⊙O的上 D．不能确定
2、如图，的直径为10，弦的长为6，为弦上的动点，则线段长的取值范围是（ ）

A. B. C. D.
3、如图，在⊙O中所对的圆周∠ACB＝67°，点P在劣弧上，∠AOP＝42°，则∠BOP的度数为（　　）

A．25° B．90° C．92° D．109°
4、如图，已知△ABC内接于⊙O，BC是⊙O的直径，AD平分∠BAC，交⊙O于D，若BC＝4，则CD的长为（　　）

A．2 B． C．3 D．
5、如图，AC是⊙O的直径，弦BD⊥AC于点E，连接BC过点O作OF⊥BC于点F，若BD＝12cm，AE＝4cm，则OF的长度是（　　）

A． B． C． D．3cm
6、如图，、切于点、，，切于点，交、于、两点，
则的周长是（ ）

A．10 B．18 C．20 D．22
7、如图，是的外接圆，交于点E，垂足为点D，，的延长线交于点F．若，，则的长是（ ）

A．10 B．8 C．6 D．4
8、如图，分别以正五边形ABCDE的顶点A，D为圆心，以AB长为半径作，，若AB＝1，则阴影部分图形的周长是（　　）

A．π+1 B．π C．π+1 D．π
9、把边长为2+的正方形沿过中心的一条直线折叠，两旁重叠部分恰为正八边形的一半，则这个正八边形的边EF的长为（　　）

A．1 B．2 C． D．2
10、如图，边长为2的正方形ABCD的中心与半径为2的⊙O的圆心重合，E，F分别是AD，BA的延长线与⊙O的交点，则图中阴影部分的面积为（　　）

A．2π﹣2 B．2π﹣2 C．2π+2 D．2π+2
二、填空题
11、已知一点到圆周上点的最大距离为，最短距离为，则圆的直径为________．
12、已知圆锥的底面半径是4，母线长是5，则该圆锥的侧面积是　 　（结果保留π）．
13、如图，△ABD内接于⊙O，∠ADB＝90°，∠ADB的角平分线DC交⊙O于C．若BD＝8，BC＝，则AD的长为 　　．

14、一条弦恰好等于圆的半径，则这条弦所对的圆周角为 　 　．
15、如图，平面直角坐标系xOy中，点A的坐标为（12，6.5），⊙A与x轴相切，点P在y轴正半轴上，PB与⊙A相切于点B．若∠APB＝30°，则点P的坐标为 　 　．

16、已知四边形ABCD内接于⊙O，OA＝5，AB＝BC，E为CD上一点，且BE＝BC，∠ABE＝90°，则AD的长为　 ．

17、如图，在平面直角坐标系中，点A的坐标是（20，0），点B的坐标是（16，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，则点C的坐标为　 　．

18、如图，MN为⊙O的直径，A、B是⊙O上的两点，过A作AC⊥MN于点C，过B作BD⊥MN于点D，P为DC上的任意一点，若MN=20，AC=8，BD=6，则PA+PB的最小值是____________．

19、如图，AB是⊙O的弦，点C在上，点D是AB的中点．将沿AC折叠后恰好经过点D，若⊙O的半径为2，AB＝8．则AC的长是　 　．

20、如图，CD为⊙O的直径，AB为⊙O中长度为定值的弦，AB＜CD．作AE⊥CD于E，连接AC，BC，BE．下列四个结论中：①O到AB的距离为定值；②BE＝BC；③当OE＝AE时，∠ABC＝67.5°或22.5°；④∠BAE+2∠ACD为定值．正确的是 　 　．（填所有正确的序号）

三、解答题
21、已知AB是⊙O的直径，CD是⊙O的弦，连接BD．
（Ⅰ）如图①，连接OC，AD．若∠ADC＝56°，求∠CDB及∠COB的大小；
（Ⅱ）如图②，过点C作DB的垂线，交DB的延长线于点E，连接OD．若∠ABD＝2∠CDB，∠ODC＝20°，求∠DCE的大小．






22、已知：如图，圆O是△ABC的外接圆，AO平分∠BAC．
（1）求证：△ABC是等腰三角形；
（2）当OA＝4，AB＝6，求边BC的长．






23、如图，⊙O是△ABC的外接圆，AB＝AC，CD⊥AB于点D，BO的延长线交CD于点E，交⊙O于另一点F．
（1）求证：∠DBE＝∠BCD．
（2）若BC＝4，BE＝4，求AB的长．









24、如图，四边形ABCD为菱形，以AD为直径作⊙O交AB于点F，连接DB交⊙O于点H，E是BC上一点，且BE＝BF，连接DE．
（1）求证DE是⊙O的切线；
（2）若BF＝1，BD＝，则菱形ABCD的面积为 　 　．





25、如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连结BE．
（1）求证：BE是⊙O的切线；
（2）设OE交⊙O于点F，若DF＝2，BC＝，求劣弧BC的长．








26、如图，⊙O是△ABC的外接圆，AB＝AC，CD⊥AB于点D，BO的延长线交CD于点E，交⊙O于另一点F．
（1）求证：∠DBE＝∠BCD．
（2）若BC＝4，BE＝4，求AB的长．







27、如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．
（1）求证：AE＝ED；
（2）若AB＝6，∠CBD＝30°，求图中阴影部分的面积．









28、已知：内接于，，于点，连接．
（1）如图，求证：；

（2）如图，延长交于点，连接，若，求证：；

（3）如图，在（2）的条件下，若，，求线段的长．















答案解析
一、选择题
1、已知⊙O的直径为10，点P到点O的距离大于8，那么点P的位置（ ）
A．一定在⊙O的内部 B．一定在⊙O的外部 C．一定在⊙O的上 D．不能确定
试题分析：的直径为10，半径为5，点到点的距离大于8，点一定在的外部，
故选B．

2、如图，的直径为10，弦的长为6，为弦上的动点，则线段长的取值范围是（ ）

A. B. C. D.
【答案】C
【解析】
【分析】由垂线段最短可知当OP⊥AB时最短，当OP是半径时最长．根据垂径定理求最短长度．
【详解】解：如图，连接OA，作OP⊥AB于P，
∵⊙O的直径为10，
∴半径为5，
∴OP的最大值为5，
∵OP⊥AB于P，
∴AP=BP，
∵AB=6，
∴AP=3，
在Rt△AOP中，OP=；
此时OP最短，
所以OP长的取值范围是4≤OP≤5．
故选：C．


3、如图，在⊙O中所对的圆周∠ACB＝67°，点P在劣弧上，∠AOP＝42°，则∠BOP的度数为（　　）

A．25° B．90° C．92° D．109°
【思路引导】根据圆周角定理得出∠AOB＝2∠ACB，求出∠AOB的度数，再求出答案即可．
【完整解答】解：∵∠ACB＝67°，
∴∠AOB＝2∠ACB＝134°，
∵∠AOP＝42°，
∴∠BOP＝∠AOB﹣∠AOP＝134°﹣42°＝92°，
故选：C．

4、如图，已知△ABC内接于⊙O，BC是⊙O的直径，AD平分∠BAC，交⊙O于D，若BC＝4，则CD的长为（　　）

A．2 B． C．3 D．
【思路引导】连接BD，根据圆周角定理得到∠BAC＝∠BDC＝90°，根据角平分线的定义得到∠BAD＝∠CAD，推出△DBC是等腰直角三角形，根据等腰直角三角形的性质即可得到答案．
【完整解答】解：连接BD，
∵BC是⊙O的直径，
∴∠BAC＝∠BDC＝90°，
∵AD平分∠BAC，
∴∠BAD＝∠CAD，
∴＝，
∴BD＝CD，
∴△DBC是等腰直角三角形，
∴CD＝BC＝2，
故选：B．


5、如图，AC是⊙O的直径，弦BD⊥AC于点E，连接BC过点O作OF⊥BC于点F，若BD＝12cm，AE＝4cm，则OF的长度是（　　）

A． B． C． D．3cm
【分析】连接OB，根据垂径定理求出BE，根据勾股定理求出OB，再根据勾股定理计算即可．
【解答】解：连接OB，
∵AC是⊙O的直径，弦BD⊥AC，
∴BE＝BD＝6，
在Rt△OEB中，OB2＝OE2+BE2，即OB2＝（OB﹣4）2+62，
解得，OB＝，
则EC＝AC﹣AE＝9，
BC＝＝3，
∵OF⊥BC，
∴CF＝BC＝，
∴OF＝＝（cm），
故选：A．


6、如图，、切于点、，，切于点，交、于、两点，
则的周长是（ ）

A．10 B．18 C．20 D．22
【分析】根据切线长定理得出PA=PB=10，CA=CE，DE=DB，求出△PCD的周长是PC+CD+PD=PA+PB，代入求出即可．
【详解】
解：∵PA、PB切⊙O于点A、B，CD切⊙O于点E，
∴PA=PB=10，CA=CE，DE=DB，
∴△PCD的周长是PC+CD+PD=PC+AC+DB+PD=PA+PB=10+10=20．
故选C．
7、如图，是的外接圆，交于点E，垂足为点D，，的延长线交于点F．若，，则的长是（ ）

A．10 B．8 C．6 D．4
【答案】A
【分析】先据垂径定理可得，再利用勾股定理可得，然后根据三角形中位线定理即可得．
【详解】解：，，
，，，，，，
又，是的中位线，，故选：A．

8、如图，分别以正五边形ABCDE的顶点A，D为圆心，以AB长为半径作，，若AB＝1，则阴影部分图形的周长是（　　）

A．π+1 B．π C．π+1 D．π
【思路引导】由五边形ABCDE可得出，AB＝BC＝CD＝DE＝EA＝1、∠A＝∠D＝108°，利用弧长公式可求出和的长度，再根据周长的定义，即可求解．
【完整解答】解：∵五边形ABCDE为正五边形，AB＝1，
∴AB＝BC＝CD＝DE＝EA＝1，∠A＝∠D＝108°，
∴的长＝的长＝＝π，
∴阴影部分图形的周长＝的长+的长+BC＝π+1．
故选：A．

9、把边长为2+的正方形沿过中心的一条直线折叠，两旁重叠部分恰为正八边形的一半，则这个正八边形的边EF的长为（　　）

A．1 B．2 C． D．2
【思路引导】重叠部分为正八边形的一半，则△CGF、△B'EF是全等的等腰直角三角形，设CG＝x，则GF＝x，B'F＝x，从而BC＝x+x+x＝2+，即可解决问题．
【完整解答】解：如图，

∵重叠部分为正八边形的一半，
∴GF＝EF＝PE＝HP，∠GFE＝∠FEP＝∠HPE＝135°，
∴∠GFC＝∠B'FE＝∠DEP＝∠A'PH＝45°，
∴△CGF、△B'EF是全等的等腰直角三角形，
设CG＝x，则GF＝x，B'F＝x，
∴BG＝B'G＝x+x，
∴BC＝x+x+x＝2+，
∴x＝1，
∴GF＝，
故选：C．

10、如图，边长为2的正方形ABCD的中心与半径为2的⊙O的圆心重合，E，F分别是AD，BA的延长线与⊙O的交点，则图中阴影部分的面积为（　　）

A．2π﹣2 B．2π﹣2 C．2π+2 D．2π+2
【思路引导】延长DC，CB交⊙O于M，N，根据圆和正方形的面积公式即可得到结论．
【完整解答】解：延长DC，CB交⊙O于M，N，连接OF，过点O作OH⊥AB于H．
在Rt△OFH中，FH＝＝＝，
∵AH＝BH＝，
∴AF＝﹣，
∴S△DAF＝•AD•AF＝×2×（﹣）＝2﹣2，
则图中阴影部分的面积＝×（S圆O﹣S正方形ABCD）﹣S△ADF＝•[π•（2）2﹣2×2]﹣（2﹣2）＝2π﹣2，
故选：A．


二、填空题
11、已知一点到圆周上点的最大距离为，最短距离为，则圆的直径为________．
【答案】或
【解析】
【分析】分点在圆内和圆外两种情况：当点在圆内时，最大距离与最小距离的和等于直径；当点在圆外时，最大距离与最小距离的差等于直径．由此即可解答.
【详解】当点在圆内时，圆的直径为9+1=10；
当点在圆外时，圆的直径为9-1=8．
故答案是：10或8．

12、已知圆锥的底面半径是4，母线长是5，则该圆锥的侧面积是　 　（结果保留π）．
【分析】圆锥的侧面积＝底面周长×母线长÷2．
【解答】解：∵底面圆的半径为4，
∴底面周长＝8π，
∴侧面面积＝×8π×5＝20π．
故答案为：20π．

13、如图，△ABD内接于⊙O，∠ADB＝90°，∠ADB的角平分线DC交⊙O于C．若BD＝8，BC＝，则AD的长为 　　．

【思路引导】连接AC，根据圆周角定理得到AB为⊙O的直径，求得∠ACB＝90°，根据角平分线的定义得到∠ADC＝∠BDC，得到AC＝BC＝5，求得AB＝AC＝10，根据勾股定理即可得到答案．
【完整解答】解：连接AC，
∵∠ADB＝90°，
∴AB为⊙O的直径，
∴∠ACB＝90°，
∵CD平分∠ADB，
∴∠ADC＝∠BDC，
∴＝，
∴AC＝BC＝5，
∴AB＝AC＝10，
∵BD＝8，
∴AD＝＝6，
故答案为：6．


14、一条弦恰好等于圆的半径，则这条弦所对的圆周角为 　 　．
【分析】根据⊙O的一条弦长恰好等于半径知：这条弦和两条半径组成了等边三角形．所以这条弦所对的圆心角是60°，再根据弦所对的圆周角有两种情况讨论求解．
解：根据题意，弦所对的圆心角是60°，
①当圆周角的顶点在优弧上时，则圆周角＝×60°＝30°；
②当圆周角的顶点在劣弧上时，则根据圆内接四边形的性质，和第一种情况的圆周角是互补，等于150°．
故答案为：30°或150°．

15、如图，平面直角坐标系xOy中，点A的坐标为（12，6.5），⊙A与x轴相切，点P在y轴正半轴上，PB与⊙A相切于点B．若∠APB＝30°，则点P的坐标为 　 　．

【思路引导】连接AB，过点A分别作AC⊥x轴、AD⊥y轴，利用根据圆的切线性质可知△PAB、△AOC为直角三角形，AB＝AC＝6.5，利用直角三角形中30°角的性质和勾股定理分别求出AP、AD的长度，进而求出OD、PD的长度即可求得答案．
【完整解答】解：过点A分别作AC⊥x轴于点C、AD⊥y轴于点D，连接AB，
当点P在点D是上方时，如图，

∵AD⊥y轴，AC⊥x轴，
∴四边形ADOC为矩形，
∴AC＝OD，OC＝AD，
∵⊙A与x轴相切，
∴AC为⊙A的半径，
∵点A坐标为（12，6.5），
∴AC＝OD＝6.5，OC＝AD＝12，
∵PB是切线，
∴AB⊥PB，
∵∠APB＝30°，
∴PA＝2AB＝13，
在Rt△PAD中，根据勾股定理得，
PD＝＝＝5，
∴OP＝PD+DO＝11.5，
∵点P在y轴的正半轴上，
∴点P坐标为（0，11.5），
故答案为：（0，11.5）．


16、已知四边形ABCD内接于⊙O，OA＝5，AB＝BC，E为CD上一点，且BE＝BC，∠ABE＝90°，则AD的长为　 ．

【思路引导】如图，连接OD，AC．首先证明∠ACE＝∠ABE＝45°，推出∠AOD＝2∠ACE＝90°，可得结论．
【完整解答】解：如图，连接OD，AC．

∵BA＝BE＝BC，
∴点B是△AEC的外接圆的圆心，
∴∠ACE＝∠ABE＝45°，
∴∠AOD＝2∠ACE＝90°，
∵OA＝OD＝5，
∴AD＝5，
故答案为：5．

17、如图，在平面直角坐标系中，点A的坐标是（20，0），点B的坐标是（16，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，则点C的坐标为　 　．

【分析】过点M作MF⊥CD于点F，则CF＝CD＝8，过点C作CE⊥OA于点E，由勾股定理可求得MF的长，从而得出OE的长，然后写出点C的坐标．
【解答】解：∵四边形OCDB是平行四边形，B（16，0），
∴CD∥OA，CD＝OB＝16，
过点M作MF⊥CD于点F，则CF＝CD＝8，
过点C作CE⊥OA于点E，
∵MN⊥CD，CD∥OB，
∴MN⊥OB，
∴∠CNM＝∠EMN＝90°，
又∵∠OEM＝90°，
∴四边形CEMN是矩形，
∵A（20，0），
∴OE＝OM﹣ME＝OM﹣CF＝10﹣8＝2．
连接MC，则MC＝OA＝10，
∴在Rt△CMF中，由勾股定理得MF＝＝6
∴点C的坐标为（2，6）
故答案为：（2，6）．


18、如图，MN为⊙O的直径，A、B是⊙O上的两点，过A作AC⊥MN于点C，过B作BD⊥MN于点D，P为DC上的任意一点，若MN=20，AC=8，BD=6，则PA+PB的最小值是____________．

【答案】
【解析】
【分析】先求出⊙O的半径，连接OA、OB，根据勾股定理求出OD、OC，即可求出CD，作点B关于MN的对称点B′，连接AB′，根据两点之间线段最短可得AB′即为PA＋PB的最小值，利用勾股定理求值即可．
【详解】解：∵MN＝20，
∴⊙O的半径＝10，
连接OA、OB，在Rt△OBD中，OB＝10，BD＝6，
∴OD＝＝＝8；
同理，在Rt△AOC中，OA＝10，AC＝8，
∴OC＝＝＝6，
∴CD＝8＋6＝14，
作点B关于MN的对称点B′，
连接AB′，则AB′即为PA＋PB的最小值，
B′D＝BD＝6，过点B′作AC的垂线，交AC的延长线于点E，
在Rt△AB′E中，
∵AE＝AC＋CE＝8＋6＝14，B′E＝CD＝14，
∴AB′＝＝＝14
故答案为：14．


19、如图，AB是⊙O的弦，点C在上，点D是AB的中点．将沿AC折叠后恰好经过点D，若⊙O的半径为2，AB＝8．则AC的长是　 　．

【思路引导】如图，延长BO交⊙O 于E，连接AE，OA，OD，OC，BC，作CH⊥AB于H．首先证明∠CAE＝∠CAH＝45°，推出∠BOC＝90°，推出BC＝2，设AH＝CH＝x，则BH＝8﹣x，在Rt△BCH中，根据CH2+BH2＝BC2，构建方程求出x即可解决问题；
【完整解答】解：如图，延长BO交⊙O 于E，连接AE，OA，OD，OC，BC，作CH⊥AB于H．
∵AD＝DB，
∴OD⊥AB，
∴∠ADO＝90°，
∵OA＝2，AD＝DB＝4，
∴OD＝＝2，
∵BE是直径，
∴∠BAE＝90°，
∵AD＝DB，EO＝OB，
∴OD∥AE，AE＝2OD＝4，
∴AE＝AD，
∴＝，
∴＝，
∴∠CAE＝∠CAH＝45°，
∴∠BOC＝2∠CAB＝90°，
∴BC＝OC＝2，
∵CH⊥AB，
∴∠CAH＝∠ACH＝45°，
∴AH＝CH，设AH＝CH＝x，则BH＝8﹣x，
在Rt△BCH中，∵CH2+BH2＝BC2，
∴x2+（8﹣x）2＝（2）2，
∴x＝6或2（舍弃），
在Rt△ACH中，∵AC＝，
∴AC＝6．
故答案为6．

20、如图，CD为⊙O的直径，AB为⊙O中长度为定值的弦，AB＜CD．作AE⊥CD于E，连接AC，BC，BE．下列四个结论中：①O到AB的距离为定值；②BE＝BC；③当OE＝AE时，∠ABC＝67.5°或22.5°；④∠BAE+2∠ACD为定值．正确的是 　 　．（填所有正确的序号）

【思路引导】①正确，利用勾股定理解决问题即可．
②错误，寻找特殊位置说明即可．
③正确，分两种情形求解即可．
④正确．证明∠BAE+2∠ACD＝90°﹣∠OAB，可得结论．
【完整解答】解：如图1中，

∵OH⊥AB，
∴AH＝BH，
∴OH＝，
∵OB，BH是定值，
∴OH是定值，故①正确，
当＝时，CD⊥AB，此时A，E，B关系，BC＞BE，故②错误，
如图2中，连接AO，AD．

当AE＝OE时，∵AE⊥OE，
∴∠AOE＝∠OAE＝45°，
∵OA＝OD，
∴∠OAD＝∠D＝67.5°，
∴∠ABC＝∠D＝67.5°，
如图3中，当AE＝OE时，连接OA，AD，

∵AE⊥OE，
∴∠AOE＝∠OAE＝45°，
∵OA＝OD，
∴∠OAD＝∠D＝22.5°，
∴∠ABC＝∠D＝22.5°，
综上所述，∠ABC＝67.5°或22.5°，故③正确，
如图4中，连接AO．

∵OA＝OC，
∴∠OAC＝∠OCA，
∴∠AOE＝∠OAC+∠OCA＝2∠ACD，
∵AE⊥EC，
∴∠AEO＝90°，
∴∠BAE+∠OAB+∠AOE＝90°，
∴∠BAE+2∠ACD＝90°﹣∠OAB，
∵∠OAB是定值，
∴∠BAE+2∠ACD是定值，故④正确，
故答案为：①③④．

三、解答题
21、已知AB是⊙O的直径，CD是⊙O的弦，连接BD．
（Ⅰ）如图①，连接OC，AD．若∠ADC＝56°，求∠CDB及∠COB的大小；
（Ⅱ）如图②，过点C作DB的垂线，交DB的延长线于点E，连接OD．若∠ABD＝2∠CDB，∠ODC＝20°，求∠DCE的大小．

【分析】（1）由直径所对的圆周角是直角可得∠CDB的度数，再利用圆周角与圆心角的关系可得答案；（2）由半径的关系可得∠ODB＝∠OBD，再利用∠ABD＝2∠CDB，∠ODC＝20°可得∠CDB＝20°，最后根据直角三角形锐角互余可得答案．
【解析】（Ⅰ）∵AB是⊙O的直径，∴∠ADB＝90°，
∵∠ADC＝56°，∴∠CDB＝90°﹣∠ADC＝90°﹣56°＝34°，
在⊙O中，∠COB＝2∠CDB＝2×34°＝68°．
（II ）∵OD＝OB，∴∠ODB＝∠OBD，即∠ODC+∠CDB＝∠OBD，
∵∠ABD＝2∠CDB，∠ODC＝20°，∴20°+∠CDB＝2∠CDB，∴∠CDB＝20°，
∵CE⊥DE，∴∠CED＝90°，在Rt△CDE中，∠DCE＝90°﹣∠CDE＝90°﹣20°＝70°．
22、已知：如图，圆O是△ABC的外接圆，AO平分∠BAC．
（1）求证：△ABC是等腰三角形；
（2）当OA＝4，AB＝6，求边BC的长．

【答案】（1）见解析；（2）3
【分析】（1）连接OB、OC，先证明∠OBA＝∠OCA＝∠BAO＝∠CAO，再证明△OAB≌△OAC得AB＝AC，问题得证；（2）延长AO交BC于点H，先证明AH⊥BC，BH＝CH，设OH＝b，BH＝CH＝a，根据OA＝4，AB＝6，由勾股定理列出a、b的方程组，解得a、b，便可得BC．
【解析】解：（1）连接OB、OC，∵OA＝OB＝OC，OA平分∠BAC，∴∠OBA＝∠OCA＝∠BAO＝∠CAO，
在△OAB和△OAC中， ，∴△OAB≌△OAC（AAS），
∴AB＝AC，即△ABC是等腰三角形；

（2）延长AO交BC于点H，∵AH平分∠BAC，AB＝AC，∴AH⊥BC，BH＝CH，
设OH＝b，BH＝CH＝a，∵BH2+OH2＝OB2， OA＝4，AB＝6，则 　①
BH2+AH2＝AB2，OA＝4，AB＝6，则 　②
②－①得： 把代入①得：（舍）
∴BC＝2a＝3．


23、如图，⊙O是△ABC的外接圆，AB＝AC，CD⊥AB于点D，BO的延长线交CD于点E，交⊙O于另一点F．
（1）求证：∠DBE＝∠BCD．
（2）若BC＝4，BE＝4，求AB的长．

【思路引导】（1）连接CF，由题意可知∠BCF＝∠ADC＝90°，利用圆周角定理可得∠BAC＝∠BFC，根据内角和为180°可得∠ACD＝∠FBC，因为AB＝AC，所以∠ABC＝∠ACB，通过等量代换即可求解；
（2）根据角的互余可得∠FEC＝∠FCE，从而可得FE＝FC，设FC＝x，则BF＝4+x，根据勾股定理即可求解．
【完整解答】（1）证明：如图，连接CF，

∵BF为直径，
∴∠BCF＝90°，
∵CD⊥AB，
∴∠ADC＝90°，
∵∠BAC＝∠BFC，
∴∠ACD＝180°﹣∠ADC﹣∠BAC，
∠FBC＝180°﹣∠BCF﹣∠BFC，
∴∠ACD＝∠FBC，
∵AB＝AC，
∴∠ABC＝∠ACB，
∴∠DBE＝∠BCD；
（2）解：∠DBE+∠DEB＝90°，∠DEB＝∠FEC，
∴∠DBE+∠FEC＝90°，
∵∠BCD+∠FCE＝90°，∠DBE＝∠BCD，
∴∠FEC＝∠FCE，
∴FE＝FC，
设FC＝x，则BF＝4+x，
在Rt△BCF中，BC2+FC2＝BF2，即（4）2+x2＝（4+x）2，
解得x＝2，
∴BF＝6，
如图，过点A作AG⊥BC于G，

∵AB＝AC，
∴BG＝CG＝2，
∴点A、O、G在同一直线上，
∴OG＝FC＝1，
∴AG＝AO+OG＝4，
在Rt△ABG中，AB2＝AG2+BG2＝24，
∴AB＝2．

24、如图，四边形ABCD为菱形，以AD为直径作⊙O交AB于点F，连接DB交⊙O于点H，E是BC上一点，且BE＝BF，连接DE．
（1）求证DE是⊙O的切线；
（2）若BF＝1，BD＝，则菱形ABCD的面积为 　 　．

【思路引导】（1）证明△DAF≌△DCE，可得∠DFA＝∠DEC，证出∠ADE＝∠DEC＝90°，即OD⊥DE，DE是⊙O的切线．
（2）连接AH，在Rt△BDF利用勾股定理求解DF的长，再根据Rt△ADF中，利用勾股定理求解AB的长，再利用菱形的面积公式可求解．
【完整解答】（1）证明：连接DF，

∵四边形ABCD为菱形，
∴AB＝BC＝CD＝DA，AD∥BC，∠DAB＝∠C，
∵BF＝BE，
∴AB−BF＝BC−BE，
即AF＝CE，
∴△DAF≌△DCE（SAS），
∴∠DFA＝∠DEC，
∵AD是⊙O的直径，
∴∠DFA＝90°，
∴∠DEC＝90°
∵AD∥BC，
∴∠ADE＝∠DEC＝90°，
∴OD⊥DE，
∵OD是⊙O的半径，
∴DE是⊙O的切线；
（2）解：∵AD是⊙O的直径，
∴∠AHD＝∠DFA＝90°，
∴∠DFB＝90°，
在Rt△BDF中，BF＝1，BD＝，
∴DF2＝BD2−BF2＝5﹣1＝4，
∴DF＝2，
在Rt△ADF中，AD2＝DF2+AF2，
∴AB2＝22+（AB﹣1）2，
解得AB＝，
∴S菱形ABCD＝AB•DF＝×2＝5．

25、如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连结BE．
（1）求证：BE是⊙O的切线；
（2）设OE交⊙O于点F，若DF＝2，BC＝，求劣弧BC的长．

【思路引导】（1）由题意连接OC，依据垂直平分线的性质得出∠EBC＝∠ECB，进而利用切线得出∠OBE＝90°，OB⊥BE，即可求解；
（2）设⊙O的半径为R，则OD＝R﹣DF＝R﹣2，OB＝R，进而利用OD2+BD2＝OB2，得到R，最后根据三角函数求出∠BOC，从而运用劣弧BC＝得出答案．
【完整解答】（1）证明：连接OC，如图，

∵OD⊥BC，
∴CD＝BD，
∴OE为BC的垂直平分线，
∴EB＝EC，
∴∠EBC＝∠ECB
∵OB＝OC，
∴∠OBC＝∠OCB，
∴∠OBC+∠EBC＝∠OCB+∠ECB，即∠OBE＝∠OCE，
∵CE为⊙O的切线，
∴OC⊥CE，
∴∠OCE＝90°，
∴∠OBE＝90°，
∴OB⊥BE，
∵OB是半径，
∴BE是⊙O的切线；
（2）设⊙O的半径为R，则OD＝R﹣DF＝R﹣2，OB＝R，
在Rt△OBD中，BD＝BC＝，
∵OD2+BD2＝OB2，
∴，
解得R＝4，
∴OD＝2，OB＝4，
∴cos∠BOD＝，
∴∠BOD＝60°，
又OD⊥BC，OB＝OC，得∠BOC＝120°，
∴劣弧BC＝．

26、如图，⊙O是△ABC的外接圆，AB＝AC，CD⊥AB于点D，BO的延长线交CD于点E，交⊙O于另一点F．
（1）求证：∠DBE＝∠BCD．
（2）若BC＝4，BE＝4，求AB的长．

【思路引导】（1）连接CF，由题意可知∠BCF＝∠ADC＝90°，利用圆周角定理可得∠BAC＝∠BFC，根据内角和为180°可得∠ACD＝∠FBC，因为AB＝AC，所以∠ABC＝∠ACB，通过等量代换即可求解；
（2）根据角的互余可得∠FEC＝∠FCE，从而可得FE＝FC，设FC＝x，则BF＝4+x，根据勾股定理即可求解．
【完整解答】（1）证明：如图，连接CF，

∵BF为直径，
∴∠BCF＝90°，
∵CD⊥AB，
∴∠ADC＝90°，
∵∠BAC＝∠BFC，
∴∠ACD＝180°﹣∠ADC﹣∠BAC，
∠FBC＝180°﹣∠BCF﹣∠BFC，
∴∠ACD＝∠FBC，
∵AB＝AC，
∴∠ABC＝∠ACB，
∴∠DBE＝∠BCD；
（2）解：∠DBE+∠DEB＝90°，∠DEB＝∠FEC，
∴∠DBE+∠FEC＝90°，
∵∠BCD+∠FCE＝90°，∠DBE＝∠BCD，
∴∠FEC＝∠FCE，
∴FE＝FC，
设FC＝x，则BF＝4+x，
在Rt△BCF中，BC2+FC2＝BF2，即（4）2+x2＝（4+x）2，
解得x＝2，
∴BF＝6，
如图，过点A作AG⊥BC于G，

∵AB＝AC，
∴BG＝CG＝2，
∴点A、O、G在同一直线上，
∴OG＝FC＝1，
∴AG＝AO+OG＝4，
在Rt△ABG中，AB2＝AG2+BG2＝24，
∴AB＝2．

27、如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．
（1）求证：AE＝ED；
（2）若AB＝6，∠CBD＝30°，求图中阴影部分的面积．

【分析】（1）根据圆周角定理得到∠ADB＝90°，根据平行线的性质得到∠AEO＝∠ADB＝90°，即OC⊥AD，于是得到结论；
（2）连接CD，OD，根据平行线的性质得到∠OCB＝∠CBD＝30°，根据等腰三角形的性质得到∠OCB＝∠OBC＝30°，求得∠AOD＝120°，根据扇形和三角形的面积公式即可得到结论．
【解答】（1）证明：∵AB是⊙O的直径，∴∠ADB＝90°，
∵OC∥BD，∴∠AEO＝∠ADB＝90°，即OC⊥AD，又∵OC为半径，∴AE＝ED，
（2）解：连接CD，OD，
∵OC∥BD，∴∠OCB＝∠CBD＝30°，
∵OC＝OB，∴∠OCB＝∠OBC＝30°，∴∠AOC＝∠OCB+∠OBC＝60°，
∵∠COD＝2∠CBD＝60°，∴∠AOD＝120°，
∵AB＝6，∴BD＝3，AD＝3，
∵OA＝OB，AE＝ED，





28、已知：内接于，，于点，连接．
（1）如图，求证：；

（2）如图，延长交于点，连接，若，求证：；

（3）如图，在（2）的条件下，若，，求线段的长．

【答案】（1）见解析；（2）见解析；（3）．
【分析】（1）如图，连接OC，根据等腰三角形的性质可得，根据可得，根据圆周角定理可得，根据等腰三角形的性质可得，根据三角形内角和可得，即可得结论；
（2）如图，连接，过点作于点，根据垂径定理可得，根据圆周角定理可得，利用角的和差关系可得，根据等腰三角形的性质可得，根据圆周角定理可得，利用AAS可证明，根据全等三角形的性质可得，进而可得结论；
（3）延长交于点，过点作于点，交于点，连接，设，根据圆周角定理及等腰三角形的性质可得，即可得出，利用SAS可证明，根据全等三角形的性质可得，，，进而可得，可得，根据三角形内角和可得，即可得出，根据等腰三角形的性质可得，设，则，，利用ASA可证明，可得，根据直角三角形两锐角互余的关系可得，利用ASA可证明，可得，利用勾股定理列方程求出m的值即可得答案．
【详解】（1）连接，
∵，∴，
∵，∴，∴，
∵∠BAC和∠BOC分别是所对的圆周角和圆心角，∴，
∵，∴，
∵，∴，
∴，∴．

（2）连接，过点作于点，
∵，∴，
∵∠EBC和∠EAC是所对的圆周角，∴，
∵，∴=，∴，
∵，，∴，
∵，∴，
∵，，∴，
在△BOK和△OBH中，，∴，∴，∴．

（3）延长CO交于点，过点作于点，交于点，连接．
设，∴，
∴，
∵∠OBC=∠OCB=，∴，
在△BCM和△ACM中，，∴，
∴，，，
∴，∴，
∵，∴，
在中，，∠EGB=90°-∠OBC=90°-，
∴，∴，
∴，
∵，∴，
设，则，
在和中，∴，∴，
∵，∴，∴，
∴，
在△GBD和△MDN中，，∴，∴，
在中，，
在中，，
∴，解得：(舍去)，，
∴．