

12.3 乘法公式 华东师大版八年级数学上册同步练习题2(含答案)
展开12.3乘法公式 同步练习题
一.选择题
1.下列计算正确的是( )
A.(﹣a3)2=a6 B.3a+2b=5ab
C.a6÷a3=a2 D.(a+b)2=a2+b2
2.已知x的二次三项式x2+kx+9可以写成一个完全平方式,则k的值是( )
A.3 B.±3 C.6 D.±6
3.下列能用平方差公式计算的式子是( )
A.(a﹣b)(a﹣b) B.(﹣a+b)(a﹣b)
C.(﹣a﹣b)(a+b) D.(﹣a﹣b)(﹣a+b)
4.若a﹣b=2,则a2﹣b2﹣4b的值是( )
A.2 B.0 C.4 D.6
5.若x+4=2y,则代数式x2﹣4xy+4y2的值为( )
A.6 B.8 C.12 D.16
6.若a+b=﹣3,ab=﹣10,则a﹣b的值是( )
A.0或7 B.0或﹣13 C.﹣7或7 D.﹣13或13
二.填空题
7.已知x2﹣2(m+3)x+9是一个完全平方式,则m= .
8.化简:(2a﹣3)(2a+3)﹣(a﹣1)2= .
9.如果y=x2﹣3,y=﹣x2+3,那么x4﹣y4= .
10.从一个边长为2a+b的大正方形中剪出一个边长为b的小正方形,剩余的正好能剪拼成四个宽为a的长方形,那么这个长方形的长为 .
11.如图,四个完全相同的长方形围一个大正方形.已知每个长方形的周长为90,面积为30,那么图中中间阴影部分的面积为 .
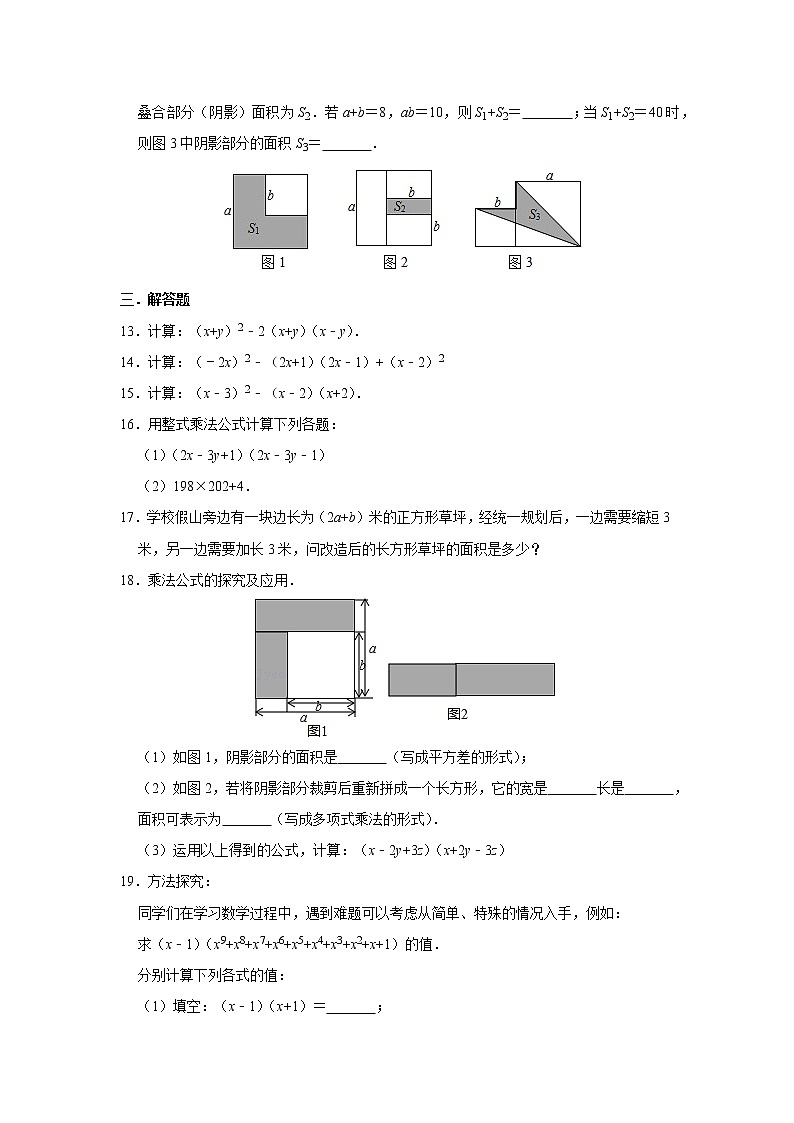
12.两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.若a+b=8,ab=10,则S1+S2= ;当S1+S2=40时,则图3中阴影部分的面积S3= .
三.解答题
13.计算:(x+y)2﹣2(x+y)(x﹣y).
14.计算:(﹣2x)2﹣(2x+1)(2x﹣1)+(x﹣2)2
15.计算:(x﹣3)2﹣(x﹣2)(x+2).
16.用整式乘法公式计算下列各题:
(1)(2x﹣3y+1)(2x﹣3y﹣1)
(2)198×202+4.
17.学校假山旁边有一块边长为(2a+b)米的正方形草坪,经统一规划后,一边需要缩短3米,另一边需要加长3米,问改造后的长方形草坪的面积是多少?
18.乘法公式的探究及应用.
(1)如图1,阴影部分的面积是 (写成平方差的形式);
(2)如图2,若将阴影部分裁剪后重新拼成一个长方形,它的宽是 长是 ,面积可表示为 (写成多项式乘法的形式).
(3)运用以上得到的公式,计算:(x﹣2y+3z)(x+2y﹣3z)
19.方法探究:
同学们在学习数学过程中,遇到难题可以考虑从简单、特殊的情况入手,例如:
求(x﹣1)(x9+x8+x7+x6+x5+x4+x3+x2+x+1)的值.
分别计算下列各式的值:
(1)填空:(x﹣1)(x+1)= ;
(x﹣1)(x2+x+1)= ;
(x﹣1)(x3+x2+x+1)= ;
…
由此可得(x﹣1)(x9+x8+x7+x6+x5+x4+x3+x2+x+1)= ;
(2)计算:1+2+22+23+…+22020+22021= ;
(3)根据以上结论,计算:5+52+53+…+52020+52021.
20.已知多项式A=x2+2x+n2,多项式B=2x2+4x+3n2+3.
(1)若多项式x2+2x+n2是完全平方式,则n2= ;
(2)已知x=m时,多项式x2+2x+n2的值为﹣1,则x=﹣m时,多项式A的值为多少?
(3)在第(2)问的条件下,求5A+[(3A﹣B)﹣2(A+B)]的值.
21.图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)图②中的阴影部分的面积为 ;
(2)观察图②,三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是 ;
(3)若x+y=﹣6,xy=2.75,则x﹣y= ;
(4)观察图③,你能得到怎样的代数恒等式呢?
(5)试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.
参考答案
一.选择题
1.解:A.(﹣a3)2=a6,故此选项符合题意;
B.3a+2b无法合并,故此选项不合题意;
C.a6÷a3=a3,故此选项不合题意;
D.(a+b)2=a2+2ab+b2,故此选项不合题意,
故选:A.
2.解:∵x的二次三项式x2+kx+9可以写成一个完全平方式,
∴x2+kx+9=(x±3)2=x2±6x+9,
∴k=±6.
故选:D.
3.解:A、(a﹣b)(a﹣b),a、b符号相同,不能用平方差公式进行计算,故此选项不合题意;
B、(﹣a+b)(a﹣b),a、b符号相反,不能用平方差公式进行计算,故此选项不合题意;
C、(﹣a﹣b)(a+b),a、b符号相反,不能用平方差公式进行计算,故此选项不合题意;
D、(﹣a﹣b)(﹣a+b),a符号相同,b的符号相反,能用平方差公式进行计算,故此选项符合题意.
故选:D.
4.解:∵a+b=2,
∴a2﹣b2﹣4b,
=(a+b)(a﹣b)﹣4b,
=2(a+b)﹣4b,
=2a﹣2b,
=2(a﹣b),
=2×2,
=4.
故选:C.
5.解:∵x+4=2y,
∴x﹣2y=﹣4,
∴x2﹣4xy+4y2=(x﹣2y)2=(﹣4)2=16.
故选:D.
6.解:∵(a﹣b)2=(a+b)2﹣4ab,
∴(a﹣b)2=(﹣3)2﹣4×(﹣10)=49,
∴a﹣b=±7.
故选:C.
二.填空题
7.解:∵x2﹣2(m+3)x+9是一个完全平方式,
∴m+3=±3,
解得:m=﹣6或m=0,
故答案为:﹣6或0
8.解:(2a﹣3)(2a+3)﹣(a﹣1)2
=(4a2﹣9)﹣(a2﹣2a+1)
=4a2﹣9﹣a2+2a﹣1
=3a2+2a﹣10,
故答案为:3a2+2a﹣10.
9.解:∵y=x2﹣3,y=﹣x2+3,
∴x2﹣3=﹣x2+3,
解得x2=3,
∴y=0,
∴x4﹣y4=9﹣0=9.
故答案为:9.
10.解:[(2a+b)2﹣b2]÷4÷a
=(2a+b+b)(2a+b﹣b)÷4÷a
=4a(a+b)÷4÷a
=a(a+b)÷a
=a+b.
故这个长方形的长为a+b.
故答案为:a+b.
11.解:设小长方形的长为a,宽为b,
则2(a+b)=90,ab=30,
∴a+b=45,
∴图中阴影部分的面积=(a+b)2﹣4ab=452﹣4×30=1905,
故答案为:1905.
12.解:由图1可得,S1=a2﹣b2,
由图2可得,S2=2b2﹣ab,
因为a+b=8,ab=10,
所以S1+S2=a2﹣b2+2b2﹣ab
=a2+b2﹣ab
=(a+b)2﹣3ab
=82﹣3×10
=64﹣30
=34;
由图3可得,S3=a2+b2﹣b(a+b)﹣a2
=a2+b2﹣ab
=(a2+b2﹣ab)
=(S1+S2)
=×40
=20;
故答案为:34,20.
三.解答题
13.解:原式=x2+2xy+y2﹣2(x2﹣y2)
=x2+2xy+y2﹣2x2+2y2
=﹣x2+2xy+3y2.
14.解:原式=4x2﹣(4x2﹣1)+x2﹣4x+4
=x2﹣4x+5.
15.解:原式=x2﹣6x+9﹣x2+4=﹣6x+13.
16.解:(1)(2x﹣3y+1)(2x﹣3y﹣1)
=(2x﹣3y)2﹣1
=4x2﹣12xy+9y2﹣1;
(2)198×202+4
=(200﹣2)×(200+2)+4
=40000﹣4+4
=40000.
17.解:(2a+b﹣3)(2a+b+3)
=(2a+b)2﹣9
=4a2+4ab+b2﹣9.
18.解:(1)利用大正方形面积减去小正方形面积即可求出:a2﹣b2;
故答案为:a2﹣b2;
(2)它的宽是 a﹣b,长是 a+b,面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a﹣b)(a+b);
(3)(x﹣2y+3z)(x+2y﹣3z);
=[x﹣(2y﹣3z)][x+(2y﹣3z)]
=x2﹣(2y﹣3z)2
=x2﹣4y2﹣9z2+12yz.
19.解:(1)(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)=x4﹣1;…
由此可得(x﹣1)(x9+x8+x7+x6+x5+x4+x3+x2+x+1)=x10﹣1;
(2)1+2+22+23+…+22020+22021
=(2﹣1)(1+2+22+23+…+22020+22021)
=22022﹣1;
故答案为x2﹣1;x3﹣1; x4﹣1;x10﹣1;22022﹣1.
(3)5+52+53+…+52020+52021=﹣1+1+5+52+53+…+52020+52021=﹣1+(5﹣1)(1+5+52+53+…+52020+52021)
=﹣1+
=.
20.解:(1)∵x2+2x+n2是一个完全平方式,
∴n2=1,
故答案为:1;
(2)当x=m时m2+2m+n2=﹣1,
∴m2+2m+1+n2=0,
∴(m+1)2+n2=0,
∵(m+1)2≥0,n2≥0,
∴x=m=﹣1,n=0,
∴x=﹣m时,多项式x2+2x+n2的值为m2﹣2m+n2=3;
(3)∵x=m=﹣1,n=0,
∴A=x2+2x+n2=﹣1,
B=2x2+4x+3n2+3=1,
∴5A+[(3A﹣B)﹣2(A+B)]
=5A+3A﹣B﹣2A﹣2B
=6A﹣3B
=6×(﹣1)﹣3×1
=﹣9.
21.解:(1)(m﹣n)2
(2)(m﹣n)2+4mn=(m+n)2
(3)±5(3分)
(4)(m+n)(2m+n)=2m2+3mn+n2
(5)答案不唯一:
例如:









