初中人教版 (五四制)30.1 图形的旋转公开课课件ppt

这是一份初中人教版 (五四制)30.1 图形的旋转公开课课件ppt，文件包含人教版五四学制9上数学301图形的旋转课件ppt、人教版五四学制9上数学301图形的旋转教案doc等2份课件配套教学资源，其中PPT共31页， 欢迎下载使用。

30.1 图形的旋转
（1）平移的定义: ，将一个图形 ，这样的图形运动叫平移.
在平面内
沿某个方向移动一定的距离
（3）平移不改变图形形状、大小、方向，只改变图形的位置.
③对应角相等． ④平移前后两图形全等．
回顾旧知，回忆平移当中的相关概念
探究一：旋转、旋转中心、旋转角、旋转方向的概念
活动1
将△ABC经平移得到△DEF（如图）
（1）平移方向是什么？（2）平移距离是多少？ （3）图中的对应点，对应线段，对应角分别有哪些？
问题：
①对应点：②对应线段：③对应角：
重点知识 ★
整合旧知，探究旋转中的相关概念
探究一：旋转、旋转中心、旋转角、旋转方向的概念
活动2
（1）① ②经过了怎样的变化？
问题：
平移
（2）① ③经过了怎样的变化？
对称
（3）① ④是平移吗？是轴对称吗？
都不是，是旋转
重点知识 ★
大胆猜想，大胆操作，探究新知
探究二：旋转的基本性质
活动1
请同学们看讲台上的大时钟，有什么在不停地转动？是绕什么点旋转呢？从现在到下课时钟转了多少度？分针转了多少度？秒针转了多少度？
问题1：
时针、分针、秒针在不停地转动，它们都绕时钟的中心转动．
如果从现在到下课时针转了_____度，分针转了_____度，秒针转了_____度．
重点、难点知识 ★▲
大胆猜想，大胆操作，探究新知
探究二：旋转的基本性质
活动1
如图，如果把钟表的指针看做三角形OAB，它绕O点按顺时针方向旋转得到△OEF，在这个旋转过程中：
问题2：
（1）旋转中心是什么？旋转角是什么？
重点、难点知识 ★▲
旋转中心是O，∠AOE、∠BOF等都是旋转角．
（2）经过旋转，点A、B分别移动到什么位置？
经过旋转，点A和点B分别移动到点E和点F的位置．
集思广益，探索旋转的基本性质
探究二：旋转的基本性质
活动2
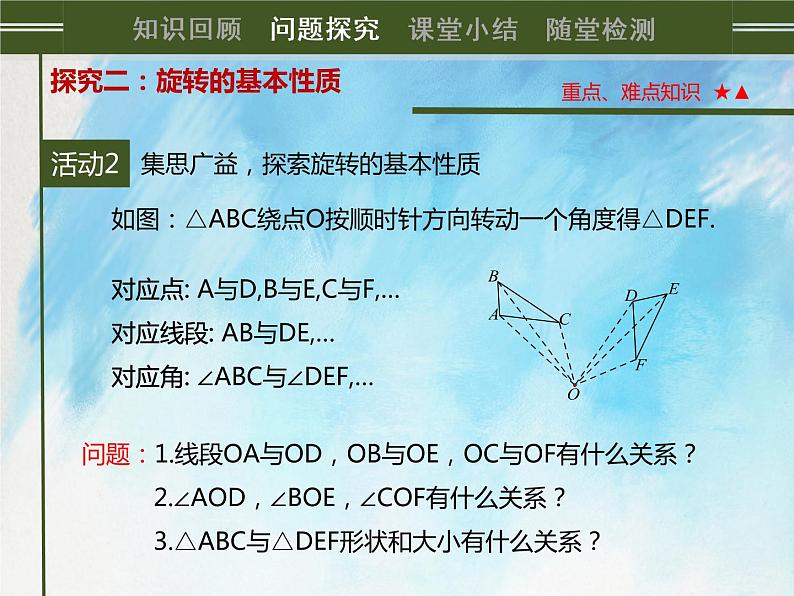
如图：△ABC绕点O按顺时针方向转动一个角度得△DEF.
对应点: 对应线段: 对应角:
重点、难点知识 ★▲
问题：1.线段OA与OD，OB与OE，OC与OF有什么关系？ 2.∠AOD，∠BOE，∠COF有什么关系？ 3.△ABC与△DEF形状和大小有什么关系？
对应点: A与D,B与E,C与F,…对应线段: AB与DE,…对应角: ∠ABC与∠DEF,…
集思广益，探索旋转的基本性质
探究二：旋转的基本性质
活动2
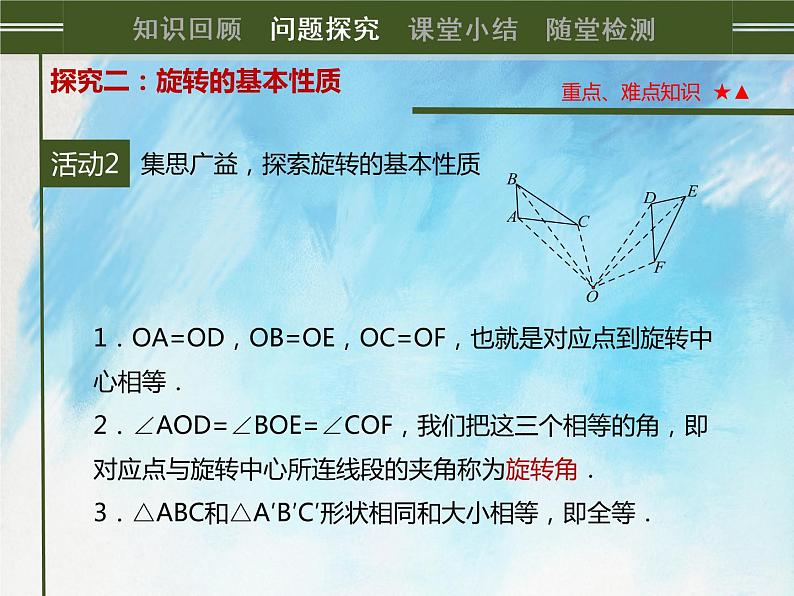
1．OA=OD，OB=OE，OC=OF，也就是对应点到旋转中心相等．2．∠AOD=∠BOE=∠COF，我们把这三个相等的角，即对应点与旋转中心所连线段的夹角称为旋转角．3．△ABC和△A′B′C′形状相同和大小相等，即全等．
重点、难点知识 ★▲
集思广益，探索旋转的基本性质
探究二：旋转的基本性质
活动2
旋转的性质：（1）对应点到旋转中心的距离相等；（2）对应点与旋转中心所连线段的夹角等于旋转角；（3）旋转前、后的图形全等．
重点、难点知识 ★▲
旋转性质应用
探究二：旋转的基本性质
活动3
1.△ABC是顶角为120°的等腰三角形, △ABD旋转至△ACE位置.
重点、难点知识 ★▲
（1）旋转中心是________（2）旋转角度是________（3）B的对应点是_______ ，BD的对应边是________，∠1的对应角是__________， ∠DAE=________.（4）连接DE, △AED是__________三角形.
【思路点拨】抓住旋转的三要素.
A
120°
C
等腰
CE
∠CAE
∠BAC
旋转性质应用
探究二：旋转的基本性质
活动3
重点、难点知识 ★▲
解：∵ ∠CAB=65°， CC'//AB ， ∴∠C'CA=∠CAB=65°.∵△ABC绕点A旋转到△AB'C'的位置∴AC=AC'，∠C'CA=∠CC'A=65°.所以∠BAB‘=∠CAC’=180°-∠C‘CA-∠CC’A＝50°.
【思路点拨】抓住旋转过程中产生的等腰三角形.
50°
旋转性质应用
探究二：旋转的基本性质
活动3
重点、难点知识 ★▲
2.②如图，△COD是△AOB绕点O按顺时针方向旋转40°得到的图形，点C恰好在AB上，∠AOD=90°，则∠B=______ .
60°
对比探究，平移与旋转的区别与联系
探究二：旋转的基本性质
活动4
重点、难点知识 ★▲
平移与旋转都是图形的变换；变换前后图形的形状，大小均不变，图形的位置要改变；平移不改变图形的方向，旋转要改变图形的方向.
练习：将图2沿MN翻折180°,再旋转180°,所得图形是( )
旋转识图
探究三：拓展应用
活动1
重点、难点知识 ★▲
例1.将图1绕O点顺时针旋转90°,得到图形是( )
D
B
【思路点拨】抓住翻折的性质和旋转的三要素是解题的关键.
提升型例题
探究三：拓展应用
活动2
重点、难点知识 ★▲
例2.如图，矩形ABCD绕C点顺时针旋转90°得到矩形CEFG， AB=4，BC=3，求AF长.
【解题过程】
【思路点拨】抓住旋转前后的对应点，构造旋转角，利用直角三角形中勾股定理求解.
提升型例题
探究三：拓展应用
活动2
重点、难点知识 ★▲
【解题过程】
【思路点拨】利用特殊的旋转角构造特殊的三角形.

30°
探究型例题
探究三：拓展应用
活动3
重点、难点知识 ★▲
例3.在Rt△ABC中，∠C=90°，∠A=30°. A、B、E在同一直线上.
⑴△ABC绕点____沿________方向旋转_____°得到△DBE.⑵若AB=2,则A点经过的路径为_______________.⑶若AB=2,则AB扫过的面积为________________.⑷若△DBE继续向右翻转到直线AB上，则从开始到结束A点经过的路径为____________________.

B
顺时针
120

探究型例题
探究三：拓展应用
活动3
重点、难点知识 ★▲
练习：一块等边三角形木块，边长为1，如图，现将木块沿水平线翻滚五个三角形，那么B点从开始至结束所走过的路径长是多少？

【解题过程】
【思路点拨】根据旋转的定义作出旋转过程中点的运动轨迹.
翻滚一次滚120°，翻滚五个三角形，正好翻滚一个圆，所以所走路径是2π．
旋转作图
探究三：拓展应用
活动4
重点、难点知识 ★▲
例4.（1）画出以下图所示的四边形ABCD以O点为中心，旋转角分别为30°、60°的旋转图形.

【解题过程】
①连结OA.②以OA为一边作∠AOA'，使得∠AOA'=30°.③在射线OA'上截取OA′=OA,则A′即为所求的A的对应点．④同理作出B'、C'、D'⑤顺次连接A'B'、B'C'、C'D'、D'A'则四边形A‘B’C‘D'即为旋转后的图形．
旋转作图
探究三：拓展应用
活动4
重点、难点知识 ★▲
例4.（1）画出以下图所示的四边形ABCD以O点为中心，旋转角分别为30°、60°的旋转图形.

【思路点拨】抓住旋转的三要素.
旋转作图
探究三：拓展应用
活动4
重点、难点知识 ★▲
（２）如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A(﹣1, 3)，B(﹣4, 0)，C(0, 0).①画出将△ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△A1B1C1；②画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O.

旋转作图
探究三：拓展应用
活动4
重点、难点知识 ★▲
①画出将△ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△A1B1C1；②画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O.

旋转作图
探究三：拓展应用
活动4
重点、难点知识 ★▲
①分别将点A、B、C向上平移1个单位，再向右平移5个单位，然后顺次连接；②根据网格结构找出点A、B、C以点O为旋转中心顺时针旋转90°后的对应点，然后顺次连接即可．

【解题过程】
【思路点拨】抓住平移和旋转的要素.
旋转作图
探究三：拓展应用
活动4
重点、难点知识 ★▲
（3）方格纸中，格点三角形甲经过旋转后得到格点三角形乙，其旋转中心是____.

【解题过程】
连接两对对应点的线段，作中垂线,交点即旋转中心.
【思路点拨】抓住对应点的连线段的中垂线交于一点.
旋转作图
探究三：拓展应用
活动4
重点、难点知识 ★▲
练习: (1)已知四边形ABCD，把四边形ABCD绕O逆时针旋转180°，请画出旋转后的图形.

旋转作图
探究三：拓展应用
活动4
重点、难点知识 ★▲

【解题过程】
①连结OA并延长.②在射线OA1上截取OA1=OA,则A1即为所求的A的对应点．③同理作出B1，C1，D1④顺次连接A1B1，B1C1，C1D1，D1A1则四边形A1B1C1D1即为旋转后的图形．
D1
A1
B1
C1
旋转作图
探究三：拓展应用
活动4
重点、难点知识 ★▲
(2)将大写字母A绕它上侧的顶点按逆时针方向旋转90°, 作出旋转后的图案, 并写出旋转前后的对应顶点、对应线段及对应角.

【解题过程】
对应顶点：A对应A，D对应D'，E对应E'，B对应B'，C对应C'.对应线段：AB对应AB'，AC对应AC'，AD对应AD'，AE对应AE'，DE对应DE'，BD对应BD'，CE对应CE'.对应角：∠BAC对应∠B'AC'，∠ADE对应∠AD'E'，∠AED对应∠AE'D'.
【思路点拨】 依次找到各特殊点的对应点，并依次连接.
旋转作图
探究三：拓展应用
活动4
重点、难点知识 ★▲
(3)在平面直角坐标系中，△A1B1C1由△ABC绕点P旋转所得，则点P的坐标为_________.

【解题过程】
连接CC1作中垂线；连接AA1作中垂线，两中垂线交点即为P(1,-1).
【思路点拨】抓住对应点的连线段的中垂线交于一点.
（1）旋转的定义：在平面内，将一个图形绕着一个定点沿某个方向转动一个角度，这样的图形运动为旋转.这个定点称为旋转中心，转动的角为旋转角.
（3）旋转的性质: ①对应点到旋转中心的距离相等； ②对应点与旋转中心所连线段的夹角等于旋转角； ③旋转前、后的图形全等．
（1）对应点到旋转中心的距离相等.即旋转中心在对应点连线段的中垂线上.（2）对应点与旋转中心的连线段所夹的角相等,都是旋转角.(找旋转角的方法)（3）对应点的连线段的中垂线交于一点,即旋转中心. (找旋转中心的方法)
点击“随堂训练→名师训练”选择“《图形的旋转》随堂检测 ”