








人教版 (五四制)九年级上册31.1 圆的有关性质优秀课件ppt
展开31.1.1 圆
一、教学目标
(一)学习目标
1.感受圆和实际生活的联系.
2.体会圆的不同定义方法.理解并掌握弧、弦、优弧、劣弧、半圆等基本概念,能够从图形中识别.
3.进一步理解点与圆的位置关系.
(二)学习重点
圆的两种定义的探索,能利用圆的知识能够解释一些生活问题.理解并掌握弧、弦、优弧、劣弧、半圆等基本概念,能够从图形中识别.
(三)学习难点
圆的运动式定义方法
二、教学设计
(一)课前设计
1.预习任务
(1)生活中的圆_________
(2)几何中的线有_________线和_________线
2.预习自测
(1)组成几何图形的基本元素是__________
【知识点】组成几何图形的基本元素
【解题过程】组成几何图形的基本元素有:点、线、面、体
【思路点拨】回顾初一内容,组成几何图形的基本元素
【答案】点,线,面,体
(2)圆是到定点的距离等于__________的点的集合,定点是__________,定长是__________
【知识点】圆的定义
【解题过程】圆的定义知,圆是到定点的距离等于定长的点的集合,定点是圆心,定长是圆的半径
【思路点拨】思考圆是怎么画出来的,其定义是什么
【答案】定长,圆心,半径
(3)圆上任意两点间的线段叫__________,圆上任意两点间的部分叫_________
【知识点】圆的相关定义
【解题过程】圆上任意两点间的线段叫弦,圆上任意两点间的部分叫弧
【思路点拨】由弦,弧的定义可得
【答案】弦,弧
(4)圆的内部可以看作到________的距离小于________的集合
【知识点】点与圆的位置关系
【数学思想】数形结合
【解题过程】圆上的点到圆心的距离等于半径,圆内的点到圆心的距离小于半径,圆外的点到圆心的距离大于半径
【思路点拨】点与圆的位置可以用距离来刻画
【答案】圆心,半径
(二)课堂设计
1.知识回顾
(1) 组成几何图形的基本元素有点,线,面,体
(2) 几何中的线有直线和曲线
2.问题探究
探究一 感受圆和实际生活的联系.
●活动① 回顾旧知,回忆学过的几何图形
学生回答:三角形,四边形
【设计意图】通过对旧知识的复习,为新知识的学习作铺垫.
●活动② 整合旧知,探究新的几何图形
师问:以上生活场景中,有哪个共同的图形?
学生回答:圆
师问:生活中,你还能举出哪些场景含有圆?
学生举手抢答
【设计意图】鼓励学生独立自主解决问题,让学生初步感受掌握几何知识的相关概念,引导学生由观察得到的感性认识,思考圆的定义
探究二 体会圆的不同定义方法.★ ▲
●活动①大胆猜想,探究新知识
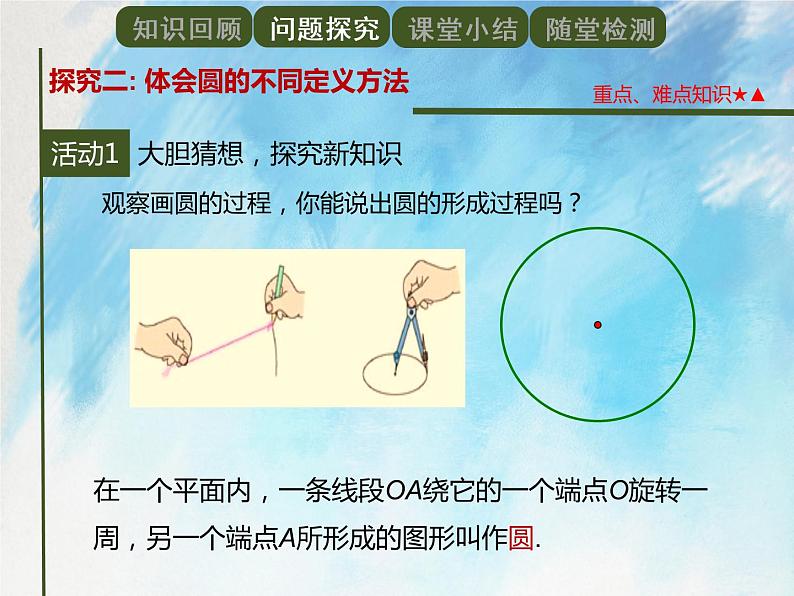
观察画圆的过程,你能说出圆的形成过程吗?(课件画图)
学生活动设计:
学生小组合作、分组讨论,通过动画演示,发现在一个平面内一条线段OA绕它的一个端点O旋转一周,另一个端点形成的图形就是圆.
教师活动设计:
在学生归纳的基础上,引导学生对圆的一些基本概念作一界定:
圆:在一个平面内,一条线段OA绕它的一个端点O旋转一周,另一个端点A所形成的图形叫作圆;
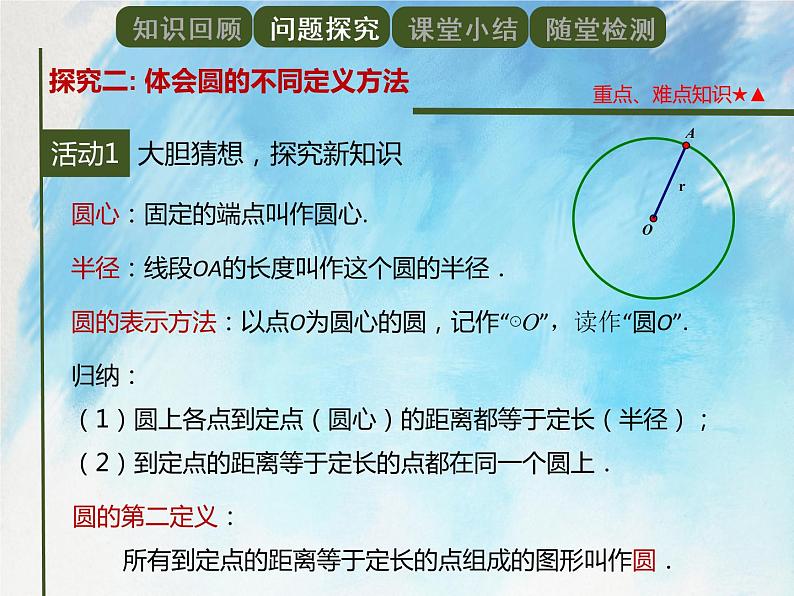
圆心:固定的端点叫作圆心;
半径:线段OA的长度叫作这个圆的半径.
圆的表示方法:以点O为圆心的圆,记作“⊙O”,读作“圆O”.
同时从圆的定义中归纳:
(1)圆上各点到定点(圆心)的距离都等于定长(半径);
(2)到定点的距离等于定长的点都在同一个圆上.
于是得到圆的第二定义:
所有到定点的距离等于定长的点组成的图形叫作圆.
【设计意图】老师综合学生的疑惑,把有意义的问题归纳,并展示出来。
●活动② 集思广益,讨论圆中相关元素的定义
如图1,你能说出弦、直径、弧、半圆的定义吗?
学生活动设计:
学生小组讨论,讨论结束后派一名代表发言进行交流,在交流中逐步完善自己的结果.
教师活动设计:
在学生交流的基础上得出上述概念的严格定义,对于学生的不准确的叙述,可以让学生讨论解决.
弦:连接圆上任意两点的线段叫作弦;
直径:经过圆心的弦叫作直径;
弧:圆上任意两点间的部分叫作圆弧,简称弧;
弧的表示方法:以A、B为端点的弧记作,读作“圆弧AB”或“弧AB”;
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫作半圆.
优弧:大于半圆的弧叫作优弧,用三个字母表示,如图1中的;
劣弧:小于半圆的弧叫作劣弧,如图1中的.
【设计意图】让学生准确认识圆中相关元素的定义
探究三 进一步理解点与圆的位置关系★ ▲
●活动1 探究点与圆的位置关系
例1. 在中,,BC=6cm,AC=8cm,以B为圆心,以BC为半径作,
问点A、C及AB、AC的中点D、E与有怎样的位置关系?
【知识点】 点与圆的位置关系,勾股定理.
【数学思想】数形结合
【解答过程】在中,,BC=6cm,AC=8cm,
,
的半径为6cm,,
点A在圆外.
,C点在圆上.
,点D在圆内,
点E在圆外.
【思路点拨】若的半径为r,点P到圆心的距离为d,当d=r,则点P在圆上;当,则点P在圆的外部;当,则点P在圆的内部,反之亦然.
当问题未附图时,可给问题配图,当问题的图形不能唯一确定时,可考虑配不同图形,分类讨论.
【答案】点A在圆外,点C在圆上,点D在圆内,点E在圆外,
练习:如图,中,,,,,以C为圆心画经过点D,则这个圆的半径应有多长?
【知识点】 点与圆的位置关系.
【数学思想】数形结合
【解答过程】由已知条件,知,,
要使经过点D,的半径应为1.5cm.
【思路点拨】若的半径为r,点P到圆心的距离为d,当d=r,则点P在圆上;当,则点P在圆的外部;当,则点P在圆的内部,反之亦然.
【答案】的半径应为1.5cm.
【设计意图】把点与圆的位置关系放在熟悉的几何图形中,进一步了解并掌握点与圆的位置关系与数形结合的思想
活动2:探究四点共圆的方法
例2.如图,四边形ABCD的一组对角,都是直角. 求证:A,B,C,D四点在同一个圆上.
【知识点】 圆的定义
【解答过程】证明:连接AC,取AC中点O,连DO,BO,在Rt△ABC中,O为斜边AC的中点,
,即OD=OA=OC.
同理:OB=OA=OC.
.
A,B,C,D四点在以O为圆心,AC为直径的圆上.
【思路点拨】四点共圆的关键体现在这四点到圆心(某一特殊点)的距离相等,从而获得该四点共圆.
练习:如图,已知中,BD,CE是两条高. 求证:B、C、D、E四点在同一圆上
【知识点】 圆的概念,直角三角形的性质.
【解答过程】证明:取BC中点O,连接EO,DO,.
在中,DO=BC
同理:,
.
B,C,D,E四点在以O为圆心,BC为直径的圆上.
【思路点拨】四点共圆的关键体现在这四点到圆心(某一特殊点)的距离相等,从而获得该四点共圆.
【设计意图】通过直角三角形斜边中线等于斜边的一半快速找到四点共圆的圆心,进一步了解圆的定义,探索证明四点共圆的方法
活动3 圆在实际生活中的应用
例3.如图,某部队在灯塔A的周围进行爆破作业,A周围3km内的水域为危险区域,有一渔民误入离A处2km的B处,为尽快驶离危险区域,该船应沿哪个方向航行?(要求给予证明)
【知识点】点与圆的位置关系,三角形的三边关系
【解答过程】该船应沿射线AB方向驶离危险区域,理由如下:
如图,设射线AB与相交于点C,在上任取一点D(不包括C关于A的对称点). 连AD,BD,在中,
,,
.
.
【思路点拨】实际应用问题,应抽象出一般的几何图形,依据圆上所有点的共同特征,结合三角形三边的关系来解决实际问题.
【答案】该船应沿射线AB方向驶离危险区域
练习:爆破时,导火索的燃烧速度为每秒0.9cm,点导火线的人要跑到离爆破点120m以外的安全区域,这个导火索的长度为18cm,那么点导火索的人每秒钟跑6.5m安全吗?
【知识点】路程与速度、时间的关系,点与圆的位置关系
【数学思想】数形结合
【解答过程】如图,圆内为危险区域. 导火索燃烧时间为,人跑的路程为,,点导火索的人非常安全.
【思路点拨】实际应用问题,应抽象出一般的几何图形,依据圆上所有点的共同特征,结合数学公式来解决实际问题.
【答案】安全
【设计意图】根据圆的定义,点与圆的位置关系,结合实际生活,解决具体问题。
3.课堂总结
知识梳理:
(1)数学来源于生活,圆与实际生活的联系
(2)圆的不同定义方法.
在一个平面内,一条线段OA绕它的一个端点O旋转一周,另一个端点A所形成的图形叫作圆
所有到定点的距离等于定长的点组成的图形叫作圆
(3)弦:连接圆上任意两点的线段叫作弦;
直径:经过圆心的弦叫作直径;
弧:圆上任意两点间的部分叫作圆弧,简称弧;
弧的表示方法:以A、B为端点的弧记作,读作“圆弧AB”或“弧AB”;
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫作半圆.
优弧:大于半圆的弧叫作优弧,用三个字母表示
劣弧:小于半圆的弧叫作劣弧
(4)若的半径为r,点P到圆心的距离为d,当d=r,则点P在圆上;当,则点P在圆的外部;当,则点P在圆的内部,反之亦然.
重难点归纳:
(1)圆的定义中:
圆上各点到定点(圆心)的距离都等于定长(半径);
到定点的距离等于定长的点都在同一个圆上
(2)点与圆的位置关系:若的半径为r,点P到圆心的距离为d,当d=r,则点P在圆上;当,则点P在圆的外部;当,则点P在圆的内部,反之亦然.
(三)课后作业
基础型 自主突破
1.圆是到定点的距离等于 的点的集合,定点是 ,定长是 .
【知识点】圆的定义
【解答过程】根据圆的定义得到
【思路点拨】圆的两要素:圆心定位置,半径定大小
【答案】定长 圆心 半径
2.圆的内部可以看作是到 距离小于 的点的集合.
【知识点】点与圆的位置关系
【解答过程】若的半径为r,点P到圆心的距离为d,当d=r,则点P在圆上;当,则点P在圆的外部;当,则点P在圆的内部,反之亦然.
【思路点拨】点的圆的位置可以通过比较点到圆心的距离与半径来确定
【答案】圆心 半径
3.确定一个圆的两个要素是 和 .
【知识点】圆的定义
【解答过程】根据圆的定义知,
【思路点拨】圆心定位置,半径定大小
【答案】圆心 半径
4.已知的直径为8cm,点A,B,C与圆心O的距离分别为4cm,3cm,5cm,则点A在 ,点B在 ,点C在 .
【知识点】点与圆的位置关系
【解答过程】∵的直径为8cm,∴半径r=4cm.∵4=4,∴点A在圆上;3<4,∴点B在圆内;∵5>4,∴点C在圆外.
【思路点拨】点的圆的位置可以通过比较点到圆心的距离与半径来确定
【答案】圆上,圆内,圆外
5.到已知点P的距离等于2cm的点的集合是 .
【知识点】圆的定义
【解答过程】根据圆的定义到定点的距离等于定长
【思路点拨】圆是到定点距离等于定长的点的集合
【答案】以P为圆心,2cm为半径的圆
6.若的半径为R,点A到圆的距离为d,当点A在圆外时,则 ;当点A在圆上时,则 ;当点A在圆内时,则 .
【知识点】点与圆的位置关系
【解答过程】若的半径为r,点P到圆心的距离为d,当d=r,则点P在圆上;当,则点P在圆的外部;当,则点P在圆的内部,反之亦然.
【思路点拨】点与圆的位置可以通过比较点到圆心的距离与半径来确定
【答案】d>R d=R d<R
能力型 师生共研
7.在中,,AB=3cm,BC=2cm,以A为圆心,以2.3cm为半径作圆,则C点和的位置关系是 .
【知识点】点与圆的位置关系
【解答过程】在中,AB=3,BC=2,,,内.
【思路点拨】点与圆的位置可以通过比较点到圆心的距离与半径来确定
【答案】点C在圆内
8.矩形的四个顶点在同一个圆上,这个圆的圆心是该矩形 ,这个圆的半径是 .
【知识点】圆的定义,矩形的性质
【解答过程】因为矩形的四个顶点到矩形对角线的交点距离相等,所以矩形对角线的交点就是圆的圆心,半径就是对角线长的一半
【思路点拨】四点共圆的关键体现在这四点到圆心(某一特殊点)的距离相等
【答案】对角线的交点 对角线长的一半
探究型 多维突破
9如图,AB是的任一直径,CD是中不过圆心的任一弦.
求证:.
【知识点】同圆半径相等 三角形三边关系
【解答过程】连接OC,OD,则OC+OD=AB,在△OCD中,OC+OD>CD,则AB>CD
【思路点拨】比较两条线段长短常见方法:三角形两边之和大于第三边,垂线段最短,两点之间,线段最短
【答案】连接OC,OD,则OC+OD=AB,在△OCD中,OC+OD>CD,则AB>CD
10.请找出图中圆的圆心,并写出你找圆心的方法.(不要求证明)
【知识点】垂直平分线的性质,圆的定义
【解答过程】有一个公共端点的两条弦的中垂线交点即为所求
【思路点拨】圆是轴对称图形,直径是它的对称轴
【答案】有一个公共端点的两条弦的中垂线交点即为所求
自助餐
1.已知的半径为5cm,A为线段OP的中点,当OP=6cm时,点A与的位置关系是( )
A. 点A在内 B. 点A在上 C. 点A在外 D. 不能确定
【知识点】点与圆的位置关系
【解答过程】根据题意OA=3cm则OA<r,所以点A在圆内
【思路点拨】点与圆的位置可以通过比较点到圆心的距离与半径来确定
【答案】A
2.已知的半径为r,点P到点O的距离大于r,那么点P的位置( )
A.一定在的内部 B. 一定在的外部 C. 一定在上 D. 不能确定
【知识点】点与圆的位置关系
【解答过程】若的半径为r,点P到圆心的距离为d,当d=r,则点P在圆上;当,则点P在圆的外部;当,则点P在圆的内部,反之亦然.
【思路点拨】点的圆的位置可以通过比较点到圆心的距离与半径来确定
【答案】B
3.如图,在中,,AC=2cm,BC=4cm,CM是中线,以C为圆心,以长为半径画圆,则A,B,C,M四点在圆外的有 ;在圆上的有 ;在圆内的有 .
【知识点】点与圆的位置关系 直角三角形斜边的中线等于斜边的一半,勾股定理
【解答过程】∵BC=4cm>,∴点B在圆外;∵∠C=90°,AC=2cm,BC=4cm,∴AB=;又∵CM是Rt的中线,∴CM=.∴点M在圆上;∵AC=2cm<,∴点A在圆内;∵C为圆心,∴点C也在圆内;
【思路点拨】点与圆的位置可以通过比较点到圆心的距离与半径来确定
【答案】点B,点M,点C和点A
4.用图形(阴影)表示到定点A的距离小于或等于2cm的点的集合.
【知识点】圆的定义 点圆的位置关系
【解答过程】
【思路点拨】到A的距离小于或等于2cm的点在以A为圆心,2cm为半径的圆上和圆
【答案】
5.如图,已知矩形ABCD的边AB=3cm,AD=4cm.
(1)以点A为圆心,4cm为半径作,则点B,C,D与的位置关系如何?
(2)若以点A为圆心作,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,则的半径r的取值范围是什么?
【知识点】点与圆的位置关系,矩形性质,勾股定理
【数学思想】数形结合
【解答过程】(1) ,B在圆内,AD=4,在圆上,,在圆外;
(2)AB=3,AD=4,AC=5,即B离A3cm是最短距离,C离A5cm最长,
【思路点拨】点的圆的位置可以通过比较点到圆心的距离与半径来确定
【答案】(1)B在圆内,D在圆上,C在圆外;(2) 3<r<5
6.两条直线a,b,已知相交于点O,AB=m,当A、B两点分别在直线,a,b上移动时,AB中点P的轨迹是怎样的?
【知识点】圆的定义 直角三角形斜边中线等于斜边一半
【解答过程】连接OP,,
为AB的中点
点的轨迹为以O为圆心,以为半径的圆.
【思路点拨】圆是到定点的距离等于定长的点的集合
【答案】点的轨迹为以O为圆心,以为半径的圆.
初中人教版 (五四制)3.1 认识圆完整版ppt课件: 这是一份初中人教版 (五四制)3.1 认识圆完整版ppt课件,共25页。PPT课件主要包含了圆的认识,dr+r,d2r,开放题等内容,欢迎下载使用。
初中数学人教版 (五四制)九年级上册32.1 随机事件与概率完美版课件ppt: 这是一份初中数学人教版 (五四制)九年级上册32.1 随机事件与概率完美版课件ppt,文件包含人教版五四学制9上数学3212概率课件ppt、人教版五四学制9上数学3212概率教案doc等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
初中数学人教版 (五四制)九年级上册第32章 概率初步32.1 随机事件与概率精品课件ppt: 这是一份初中数学人教版 (五四制)九年级上册第32章 概率初步32.1 随机事件与概率精品课件ppt,文件包含人教版五四学制9上数学3211随机事件课件ppt、人教版五四学制9上数学3211随机事件教案doc等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。













