初中数学人教版 (五四制)九年级上册31.1 圆的有关性质完整版课件ppt

这是一份初中数学人教版 (五四制)九年级上册31.1 圆的有关性质完整版课件ppt，文件包含人教版五四学制9上数学3114圆周角1教案doc、人教版五四学制9上数学3114圆周角1课件ppt等2份课件配套教学资源，其中PPT共26页， 欢迎下载使用。

31.1.4 圆周角
第一课时
（1）在同圆和等圆中，相等的圆心角所对的 相等，所对的 也相等．（2）在同圆或等圆中，如果两条弧相等，那么它们所对的 角相等，所对的 相等；（3）在同圆或等圆中，如果两条弦相等，那么它们所对的 角相等，所对的 相等．
弧
弦
圆心
弦
圆心
优（劣）弧
活动1
重点、难点知识★▲
探究一：圆周角定义，圆周角和圆心角关系
以旧引新
活动1
重点、难点知识★▲
探究一：圆周角定义，圆周角和圆心角关系
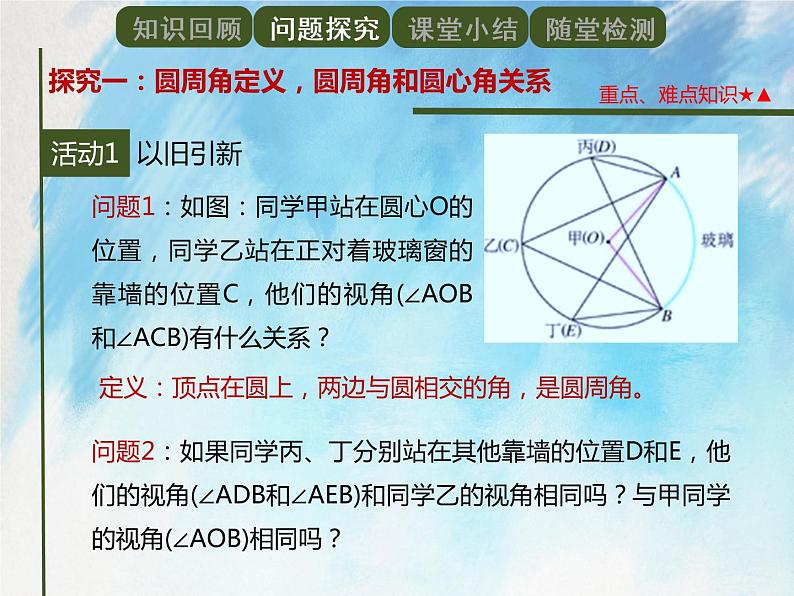
问题1：如图：同学甲站在圆心O的位置，同学乙站在正对着玻璃窗的靠墙的位置C，他们的视角(∠AOB和∠ACB)有什么关系？
以旧引新
定义：顶点在圆上，两边与圆相交的角，是圆周角。
问题2：如果同学丙、丁分别站在其他靠墙的位置D和E，他们的视角(∠ADB和∠AEB)和同学乙的视角相同吗？与甲同学的视角(∠AOB)相同吗？
活动2
重点、难点知识★▲
探究一：圆周角定义，圆周角和圆心角关系
大胆猜想，探究新知
问题1：同弧（弧AB）所对的圆心角∠AOB 与圆周角∠ACB的大小关系是怎样的？问题2：同弧（弧AB）所对的圆周角∠ACB 与圆周角∠ADB 的大小关系是怎样的？
同弧所对的圆周角的度数差不多一样，并且它的度数恰好等于这条弧所对的圆心角的度数的一半.
活动2
重点、难点知识★▲
探究一：圆周角定义，圆周角和圆心角关系
大胆猜想，探究新知
方法二： 几何证明法
在⊙O任取一个圆周角∠BAC,将圆对折，使折痕经过圆心O和∠BAC的顶点A，由于点A的位置的取法可能不同，这时折痕可能会：在圆周角的一条边上；在圆周角的内部；在圆周角的外部。
活动2
重点、难点知识★▲
探究一：圆周角定义，圆周角和圆心角关系
大胆猜想，探究新知
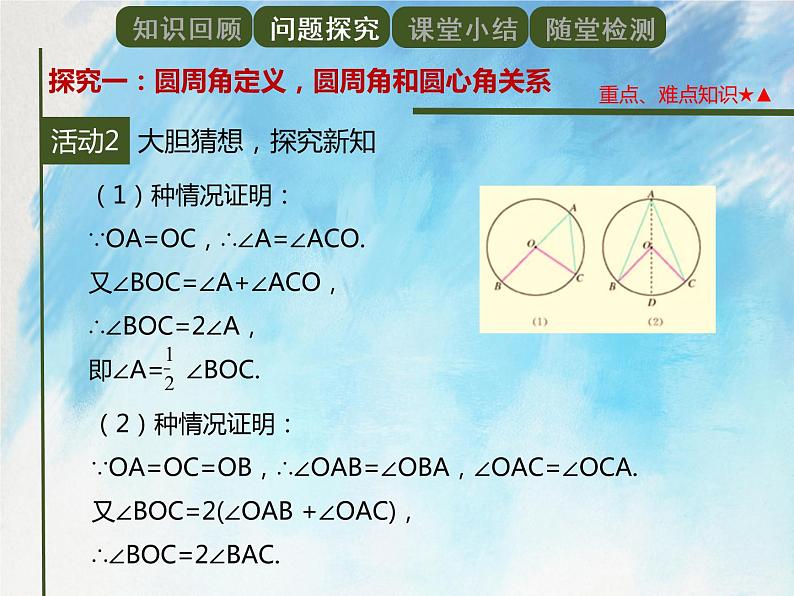
（2）种情况证明：∵OA=OC=OB，∴∠OAB=∠OBA，∠OAC=∠OCA.又∠BOC=2(∠OAB +∠OAC)，∴∠BOC=2∠BAC.
活动2
重点、难点知识★▲
探究一：圆周角定义，圆周角和圆心角关系
大胆猜想，探究新知
（3）种情况证明：∵OA=OC=OB，∴∠BAD=∠ABO，∠CAD=∠OCA.∴∠BOD=2∠BAD，∠COD=2∠CAD.∴∠BOC= ∠COD-∠BOD=2(∠CAD- ∠BAD)=2∠BAC.
定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于该弧或等弧所对圆心角度数的一半.
还可以得到：同圆或等圆中，如果两个圆周角相等，则它们的弧也相等.
活动
难点知识▲
探究二: 直径所对的圆周角
大胆猜想，探究新知
半圆（或直径）所对的圆周角是多少度呢？
90°
如图，已知BC为⊙O直径，∠BAC为圆周角，求证：∠BAC=90°.
结论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。
证明：∵∠BOC=2∠BAC=180°,∴∠BAC=90°
活动1
探究三: 圆周角的性质定理的应用
基础性例题
例1.如图，⊙O的半径为6，点A、B、C在⊙O上，且∠ACB=45°，则弦AB的长是　　　　．
【思路点拨】连接OA，OB，可以证得△AOB是等腰直角三角形，利用勾股定理即可求解．
【解题过程】
探究三: 圆周角的性质定理的应用
练习1：如图，⊙O的直径AB垂直于弦CD，∠CAB=36°，则∠BCD的大小是（　　）A．18° B．36° C．54° D．72°
【解题过程】
B
探究三: 圆周角的性质定理的应用
例2.如图，已知AB是⊙O的直径，BC为弦，过圆心O作OD⊥BC交弧BC于点D，连接DC，若∠DCB=32°，则∠BAC=　 　．
【思路点拨】由圆周角定理可知，∠BOD=2∠BCD=64°，由AB为直径可知，AC⊥BC，又OD⊥BC，可知AC∥OD，利用平行线的性质可求∠BAC．
64°
【解题过程】
探究三: 圆周角的性质定理的应用
练习2：如图，BD是⊙O的直径，∠CBD=30°，则∠A的度数为　　.
60°
【思路点拨】根据直径所对的圆周角是直角，得∠BCD=90°，然后由直角三角形的两个锐角互余、同弧所对的圆周角相等求得∠A=∠D=60°．
解：∵BD是⊙O的直径，∴∠BCD=90°（直径所对的圆周角是直角），∵∠CBD=30°，∴∠D=60°（直角三角形的两个锐角互余），∴∠A=∠D=60°（同弧所对的圆周角相等）.
【解题过程】
【思路点拨】由于三角形的外心的位置可能在三角形的内部，也可能在三角形的外部．
活动2
探究三: 圆周角的性质定理的应用
提升型例题
例3.已知点O为△ABC的外心，且∠BOC=80°，则∠BAC=　 　 　．
40°或140°
【解题过程】
探究三: 圆周角的性质定理的应用
解：连结AD，如图，∵AB是⊙O的直径，∴∠ADB=90°，∵∠ABD=55°，∴∠A=90°﹣55°=35°，∴∠BCD=∠A=35°．
练习3：如图, 若AB是⊙O的直径, CD是⊙O的弦, ∠ABD=55°，则∠BCD的度数为　 　．
【思路点拨】连结AD, 由AB是⊙O的直径得到∠ADB=90°, 再根据互余计算出∠A的度数, 然后根据圆周角定理即可得到∠C的度数.
35°
【解题过程】
探究三: 圆周角的性质定理的应用
【思路点拨】通过∠ABC=45°，可得出∠AOC=90°，根据OA=OC就可以结合勾股定理求出AC的长了．
【解题过程】
【思路点拨】根据直径所对的圆周角是直角得到∠ADB=90°，再根据直角三角形的两个锐角互余求得∠B=65°，再根据同弧所对的圆周角相等进行求解．
探究三: 圆周角的性质定理的应用
练习4：已知，如图，AB是⊙O的直径，点D，C在⊙O上，连接AD、BD、DC、AC，如果∠BAD=25°，那么∠C的度数是（　） A．75° B．65° C．60° D．50°
B
解：∵AB是⊙O的直径，∴∠ADB=90°．又∠BAD=25°，∴∠B=65°．∴∠C=65°．
【解题过程】
活动3
探究三: 圆周角的性质定理的应用
探究型例题
例5.如图, ⊙C过原点, 且与两坐标轴分别交于点A和点B, 点A的坐标为（0, 3）, M是第三象限内⊙C上一点, ∠BMO=120°, 则⊙C的半径长为　 　．
3
【解题过程】
活动3
探究三: 圆周角的性质定理的应用
探究型例题
【思路点拨】先根据圆内接四边形的性质求出∠OAB的度数，由圆周角定理可知∠AOB=90°，故可得出∠ABO的度数，根据直角三角形的性质即可得出AB的长，进而得出结论．
例5.如图, ⊙C过原点, 且与两坐标轴分别交于点A和点B, 点A的坐标为（0, 3）, M是第三象限内⊙C上一点, ∠BMO=120°, 则⊙C的半径长为　 　．
3
练习5：如图，正方形ABCD四个顶点都在⊙O上，点P是在弧AB上的一点，则∠CPD的度数是（　　） A．35° B．40° C．45° D．60°
探究三: 圆周角的性质定理的应用
C
【思路点拨】连AC, 由四边形ABCD为正方形, 得到∠CAD=45°, 由∠CPD=∠CAD=45°．
解：连接AC，如图，∵四边形ABCD为正方形，∴∠CAD=45°，又∵∠CPD=∠CAD=45°．
【解题过程】
例6.如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于D，若AC∶BC=4∶3，AB=10cm，则OD的长为　 　cm．
探究三: 圆周角的性质定理的应用
4
【解题过程】
探究三: 圆周角的性质定理的应用
【思路点拨】根据AB是直径可以得到△ABC是直角三角形，依据勾股定理即可求得AC的长，然后根据垂径定理证得D是BC的中点，则OD是△ABC的中位线，依据三角形的中位线定理即可求解．
例6.如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于D，若AC∶BC=4∶3，AB=10cm，则OD的长为　 　cm．
4
练习6：如图, ⊙O中, 弦AB, CD相交于点P, ∠A=42°, ∠APD=77°, 则∠B的大小是（　　） A．43° B．35° C．34° D．44°
【思路点拨】由同弧所对的圆周角相等求得∠A=∠D=42°，然后根据三角形外角的性质即可得到结论．
B
探究三: 圆周角的性质定理的应用
解：∵∠D=∠A=42°，∴∠B=∠APD﹣∠D=77° - 42°=35°，故选B．
【解题过程】
知识梳理
（1）把顶点在圆上，并且两边都与圆相交的角叫做圆周角。（2）在同圆或等圆中，同弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。（3）半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。
重难点突破
1.在同圆或等圆中，同弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。2.半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。
点击“随堂训练→名师训练”选择“《 圆周角（1）》随堂检测 ”