初中数学人教版八年级上册11.1.1 三角形的边教案

这是一份初中数学人教版八年级上册11.1.1 三角形的边教案，共3页。
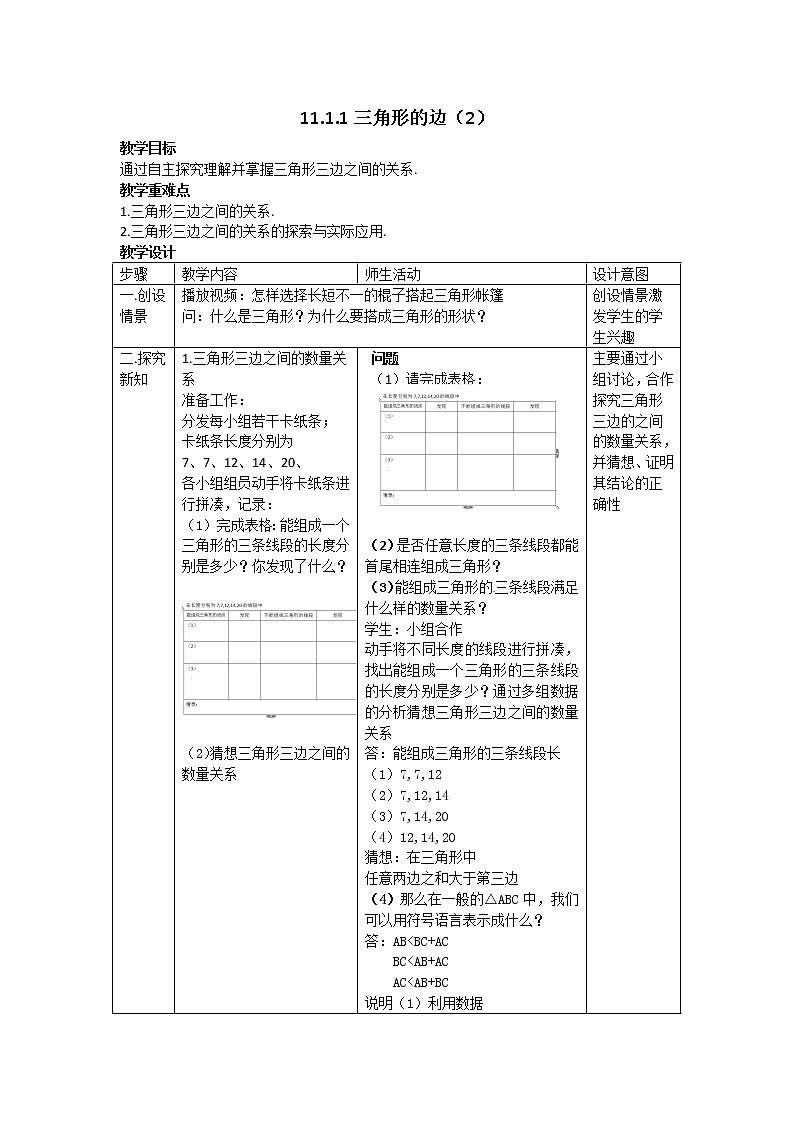
11.1.1三角形的边（2）教学目标通过自主探究理解并掌握三角形三边之间的关系.教学重难点三角形三边之间的关系.三角形三边之间的关系的探索与实际应用.教学设计步骤教学内容师生活动设计意图一.创设情景播放视频：怎样选择长短不一的棍子搭起三角形帐篷问：什么是三角形？为什么要搭成三角形的形状？ 创设情景激发学生的学生兴趣二.探究新知1.三角形三边之间的数量关系准备工作：分发每小组若干卡纸条；卡纸条长度分别为7、7、12、14、20、各小组组员动手将卡纸条进行拼凑，记录：（1）完成表格：能组成一个三角形的三条线段的长度分别是多少？你发现了什么？  （2）猜想三角形三边之间的数量关系            例1.以下列各组线段长为边，能否组成三角形？为什么?（1）1,2,4（   ）（2）8,6,4（   ）（3）12,5,7（    ）（4）2,3,6（    ）（5）2,5,6（    ）技巧：              （6）以线段2,4，a为边组成三角形，则a的取值范围为          .  例2.已知线段AB=3，BC=5，AC=a,若以AB,BC和AC为边组成三角形，则有（ ）A.2<a<8  B. C.    D. 【变式】已知三角形的三边长分别为AB=3，BC=5，AC=a,则周长L的取值范围是(   ) A.6<L<15     B.6<L<16  C.11<L<13  D.10<L<16 问题（1）请完成表格：       （2）是否任意长度的三条线段都能首尾相连组成三角形？（3）能组成三角形的三条线段满足什么样的数量关系？学生：小组合作动手将不同长度的线段进行拼凑，找出能组成一个三角形的三条线段的长度分别是多少？通过多组数据的分析猜想三角形三边之间的数量关系答：能组成三角形的三条线段长（1）7,7,12（2）7,12,14（3）7,14,20（4）12,14,20猜想：在三角形中任意两边之和大于第三边（4）那么在一般的△ABC中，我们可以用符号语言表示成什么？答：AB<BC+ACBC<AB+ACAC<AB+BC说明（1）利用数据（2）两点之间线段最短（播放视频）（3）利用卡纸条 例1：技巧：比较较短的两边之和与最长边的大小即可。（6）由两边之和大于第三边得到a<6当a=1时、当a=2时不能组成三角形，所以要组成三角形还需要满足另一个条件 （5）竟然三角形两边之和与第三边存在着这样的规律，那么两边之差与第三边又存在着什么数量关系呢？推理：因为AC<AB+BC          所以AC-BC<AB两边之差小于第三边符号语言：在△ABC中，AC-BC<AB<AC+BC   从求三角形第三边的取值范围跨越到求周长的取值范围，可以进行适当的小组讨论      2<   a   <82+(3+5)<a+(3+5)<8+(3+5)主要通过小组讨论，合作探究三角形三边的之间的数量关系，并猜想、证明其结论的正确性                         例2.已知三角形两边长度，从求三角形第三边的取值范围跨越到求周长的取值范围，隐含了周长与三角形三边的数量关系，同时考察对不等式性质的掌握 五小结 这节课你的收获是什么？     令你印象最深的是什么？    学生自由表达自己的想法，老师作                          适当的补充  六．拓展训练1.已知△ABC的两边AB=3，AC=8，（1）第三边BC的取值范围          .（2）若第三边BC长为整数，BC的长是        .（3）若△ABC周长为奇数，第三边BC的长是        .  已知△ABC三边的长分别为a,b,c，若求b的取值范围 3.如图，D是△ABC的边AC上的一点，AD=BD，（1）判断AC与BC的大小（2）若AB=AC=10，△BCD的周长为15，求BC的长       对知识综合应用的考察    3.小组讨论，小组代表上讲台讲解，其他同学提出问题  四。板书设计.