






北师大版八年级上册1 平均数教学ppt课件
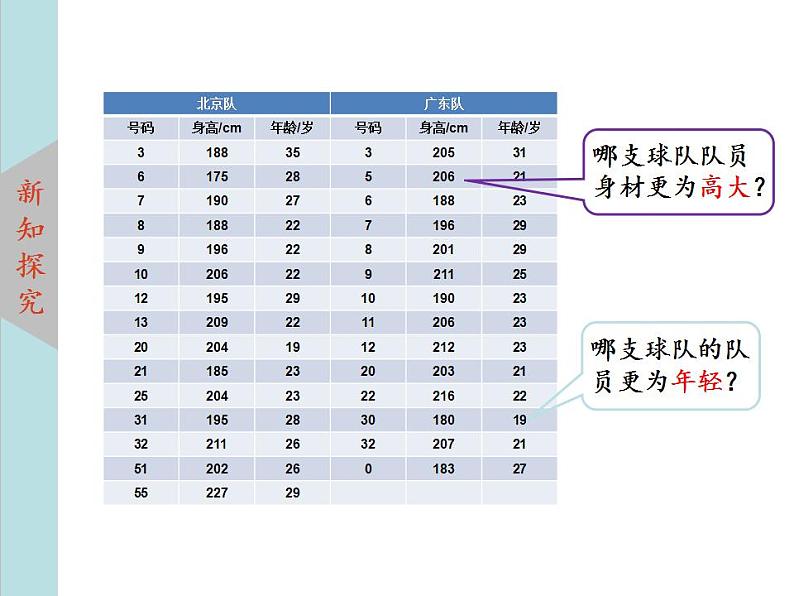
展开影响比赛的成绩有哪些因素? 如何衡量两个球队队员的身高? 怎样理解“甲队队员的身高比乙队更高”? 要比较两个球队队员的身高,需要收集哪些 数据呢?
掌握算术平均数和加权平均数的概念,会求一组数据的算术平均数;
6.1 平均数 第1课时 算数平均数和加权平均数
在篮球比赛中,队员的身高、年龄都是影响球队实力的因素,如何衡量两个球队队员的身高?
怎样理解“甲球队队员的身高比乙队更高”?怎样理解“甲队队员比乙队更年轻”?
所以广东东莞银行队的队员更为年轻.
日常生活中,我们常用平均数表示一组数据的“平均水平”,它反映了一组数据的“集中趋势”.
例1.植树节到了, 某单位组织职工开展植树竞赛, 下图反映的是植树量与人数之间的关系.
请根据图中信息计算:(1)总共有多少人参加了本次活动?(2)总共植树多少棵?(3)平均每人植树多少棵?
解:(1)参加本次活动的总人数是 1+8+1+10+8+3+1=32(人)
(2)总共植树 3×8+4×1+5×10+6×8+7×3+8×1=155(棵).
(3)平均每人植树 (棵)
小明是这样计算北京队队员的平均年龄的:
平均年龄 =(19×1+ 22×4+ 23×2+ 26×2+ 27×1+ 28×2 + 29×2+ 35×1)÷(1+4+2+2+1+2+2+1) =25.4(岁)
如果在n个数中,x1出现 f1 次,x2出现 f2次,…,xk 出现 fk 次(这里f1+f2+… + fk =n),那么
当一组数据中有若干个数据多次重复出现时,可以考虑下面的做法:
在实际问题中,一组数据里的各个数据的“重要程度” 未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“权”.
一般地,若n个数x1, x2, …, xn的权分别是f1,f2,…,fn ,则
叫做这n个数的加权平均数.
权的意义:(1)数据的重要程度 (2)权衡轻重或份量大小
例2.某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人测试成绩,此时谁将被录用?
解:A的平均成绩为(72+50+88)÷3=70(分),B的平均成绩为(85+74+45)÷3=68(分). C的平均成绩为(67+70+67)÷3=68(分). 由70>68,故A将被录用.
(2)公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人测试成绩,此时谁将被录用?
解∶A的测试成绩为∶(72×4+50×3+88×1)÷(4+3+1)=65.75(分),B的测试成绩为∶(85×4+74×3+45×1)÷(4+3+1)=75.875(分),C的测试成绩为∶(67×4+70×3+67×1)÷(4+3+1)=68.125(分). 因此候选人B将被录用.
4,3,1 分别是创新、综合知识、语言三项测试成绩的权,而称(72×4+50×3+88×1)÷(4+3+1)为A的三项测试成绩的加权平均数.
1. 某班级为了解同学年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个班级学生的平均年龄(结果取整数).
解:这个班级学生的平均年龄为:
所以,他们的平均年龄约为14岁.
2. 一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
如果公司要招聘一名笔译能力较强的翻译,那听、说、读、写成绩按2:1:3:4的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
因为79.5<80.4,所以应该录取乙.
3. 某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( )A.84 B. 86 C. 88 D. 90
4. 若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是( )A. (x+y)/2 B. (mx+ny)/(m+n) C. (x+y)/(m+n) D. (mx+ny)/(x+y)
5. 李大伯有一片果林,共有80棵果树.某日,李大伯开始采摘今年第一批成熟的果子,他随机选取2棵果树共摘得10个果子,质量分别为(单位:㎏):0.28,0.26,0.24,0.23,0.25,0.24,0.26,0.26,0.25,0.23.以此估算,李大伯收获的这批果子的单个质量和总质量分别约为( ) ㎏,200 ㎏ B.2.5 ㎏,100 ㎏ ㎏,100 ㎏ D.2.5 ㎏,200 ㎏
6. 已知:x1,x2,x3,…, x10的平均数是a,x11,x12,x13,… ,x30的平均数是b,则x1,x2,x3,… ,x30的平均数( ) A.(a+b) B.(a+b) C.(a+3b)/3 D.(a+2b)/3
7. 若x1,x2,…, xn的平均数为a, (1)则数据x1+3,x2+3,…,xn+3的平均数为 . (2)则数据10x1,10x2,… ,10xn 的平均数为 .
加权平均数: (f( f1 + f2 + …+ fk =n)
数学1 平均数教学课件ppt: 这是一份数学1 平均数教学课件ppt,共18页。PPT课件主要包含了学习目标,情景引入,请思考,探究新知,想一想,典例精讲,思考讨论,课堂练习,课堂小结等内容,欢迎下载使用。
北师大版八年级上册1 平均数习题ppt课件: 这是一份北师大版八年级上册1 平均数习题ppt课件,共18页。
北师大版1 平均数一等奖课件ppt: 这是一份北师大版1 平均数一等奖课件ppt,共21页。PPT课件主要包含了导入新知,素养目标,探究新知,问题二,巩固练习,链接中考,课堂检测,加权平均数的应用,加权平均数的影响,加权平均数的实际应用等内容,欢迎下载使用。













