初中数学北师大版八年级上册4 平行线的性质教学课件ppt

这是一份初中数学北师大版八年级上册4 平行线的性质教学课件ppt，共20页。PPT课件主要包含了知识回顾，两直线平行，平行线的性质，∵b∥a已知，∵c∥a已知，所以DFEC，所以∠BDF∠1，∠EDF∠3，因为EDAC，所以∠3∠2等内容，欢迎下载使用。

1.同位角相等2.内错角相等3.同旁内角互补
问题 平行线的判定方法是什么？
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
1. 理解并掌握平行线的性质公理和定理．2. 能熟练运用平行线的性质进行简单的推理证明．
7.4 平行线的性质
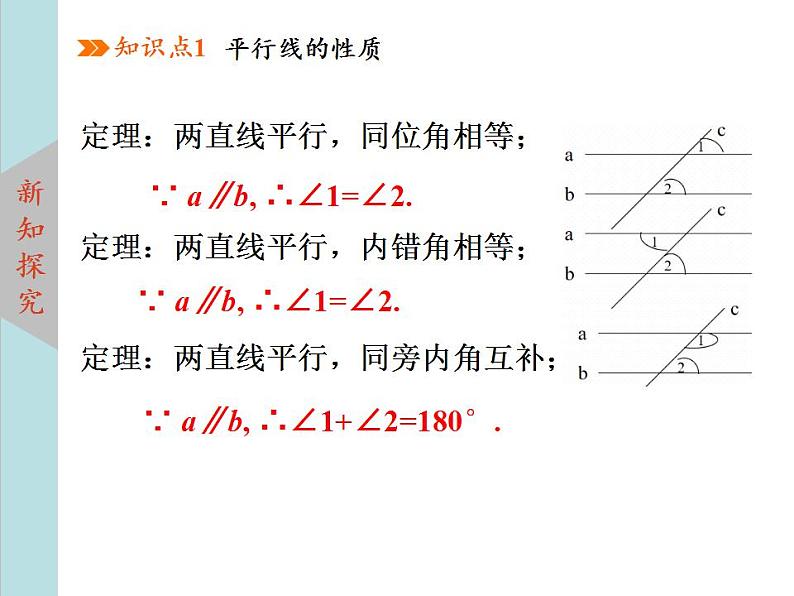
定理：两直线平行，同位角相等；定理：两直线平行，内错角相等；定理：两直线平行，同旁内角互补；
定理：两直线平行，同位角相等
已知：如图，直线AB//CD,　∠1和∠2是直线AB、CD被直线EF截出的同位角。求证：∠1＝∠2
反证法---是一种间接的证明方法
又因为AB // CD，这样经过点M存在两条直线AB和GH都与直线CD平行。
证明：假设∠1≠∠2 ，
这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾
根据“同位角相等，两直线平行”，可知GH // CD,
那么我们可以过点M作直线GH，使∠EMH= ∠2,如图所示.
在上一节中，我们利用“同位角相等，两直线平行”推出了“内错角相等，两直线平行线”，类似地，已知两直线平行，同位角相等，能否得到内错角之间的数量关系？
∵ a∥b, ∴∠1=∠2.
∵ a∥b, ∴∠1+∠2=180°.
证明的一般步骤：第一步：根据题意,画出图形．　　先根据命题的条件即已知事项，画出图形，再把命题的结论即求证的需要在图上标出必要的字母或符号，以便于叙述或推理过程的表达．第二步：根据条件、结论,结合图形,写出已知、求证.　　把命题的条件转化为几何符号的语言写在已知中，命题的结论转化为几何符号的语言写在求证中．第三步：经过分析,找出由已知推出求证的途径,写出证明过程．　
例1. 已知：如图，b∥a，c∥a，∠1，∠2，∠3是直线a，b，c被直线d截出的同位角.求证：b∥c.
∴ ∠2=∠1（两直线平行，同位角相等）.
∴ ∠2=∠3（等量代换）.
∴ ∠3=∠1（两直线平行，同位角相等）.
∴ b∥c（同位角相等，两直线平行）.
例2. 如图所示，已知四边形ABCD 中， AB∥CD， AD∥BC,试问∠A与∠C，∠B与∠D 的大小关系如何？
解：∠A= ∠ C, ∠B=∠D理由：∵AB∥CD （已知 ） ∴∠B+∠C=180°（两直线平行，同旁内角互补 ）
又 ∵ AD∥BC （已知） ∴∠C+∠D=180°（ 两直线平行，同旁内角互补 ） ∴∠ B=∠D （ 同角的补角相等 ） 同理 ∠A=∠C
5.如图，在∆ABC中，CE⊥AB于点E，DF⊥AB于点F，AC//ED，CE是∠ACB的平分线，则∠EDF=∠BDF，请说明理由.
解：因为CE⊥AB， DF⊥AB
所以∠BDF=∠EDF.
6.如图,∠BAE+∠AED=180°,∠M=∠N,那么∠1与∠2是否相等?为什么?
∵∠BAE+∠AED= 180°，∴AB//CD(同旁内角互补,两直线平行),∴∠BAE=∠AEC(两直线平行,内错角相等).
又∵∠M=∠N(已知),∴AM//NE(内错角相等,两直线平行),∴∠MAE=∠NEA(两直线平行,内错角相等),∴∠BAE- ∠MAE=∠AEC-∠ NEA即∠1=∠2.
7.如图，已知CD∥AB，∠DCB＝70°，∠CBF＝20°，∠EFB＝130°，则直线EF与AB有怎样的位置关系？为什么？
解：EF∥AB.理由如下：∵CD∥AB，∠DCB＝70°，∴∠DCB＝∠ABC＝70°.∵∠CBF＝20°，∴∠ABF＝∠ABC－∠CBF＝50°.∵∠EFB＝130°，∴∠ABF＋∠EFB＝50°＋130°＝180°.∴EF∥AB.