人教版八年级上册12.3 角的平分线的性质教课课件ppt

这是一份人教版八年级上册12.3 角的平分线的性质教课课件ppt，共15页。PPT课件主要包含了情景导入，合作探究，1角的平分线，3垂直距离，定理的作用，证明线段相等，DECD，∠DEB∠C，BEFC，当堂演练等内容，欢迎下载使用。
不利用工具，请你将一张用纸片做的角分成两个相等的角. 你有什么办法？
再打开纸片 ，看看折痕与这个角有何关系？
知识板块一　角的平分线的画法
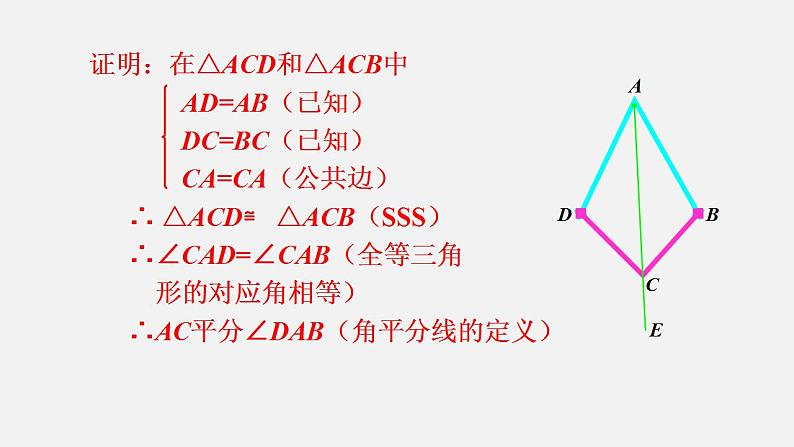
如图是一个平分角的仪器，其中AB＝AD，BC＝DC.将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线AE，AE就是这个角的平分线．你能说明它的道理吗？
证明：在△ACD和△ACB中 AD=AB（已知） DC=BC（已知） CA=CA（公共边） ∴ △ACD≌ △ACB（SSS） ∴∠CAD=∠CAB（全等三角 形的对应角相等） ∴AC平分∠DAB（角平分线的定义）
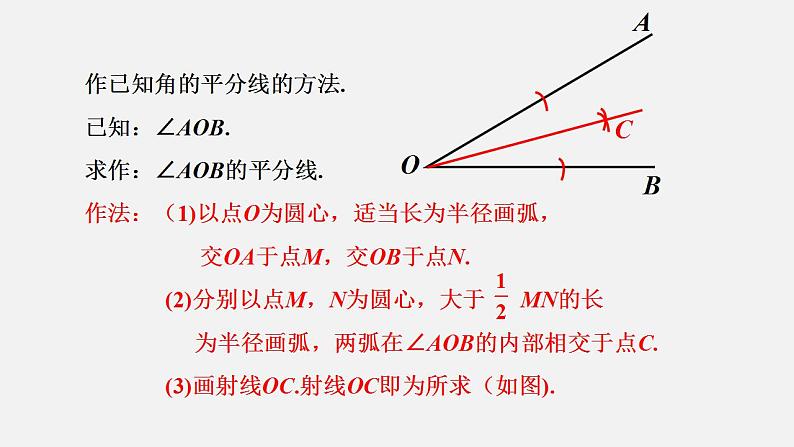
作已知角的平分线的方法.已知：∠AOB.求作：∠AOB的平分线.作法：（1)以点O为圆心，适当长为半径画弧， 交OA于点M，交OB于点N. (2)分别以点M，N为圆心，大于 MN的长 为半径画弧，两弧在∠AOB的内部相交于点C. (3)画射线OC.射线OC即为所求（如图).
知识板块二　角的平分线的性质
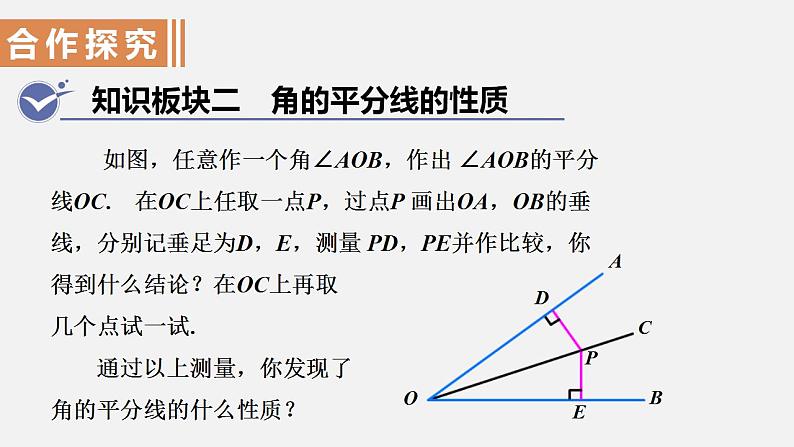
如图，任意作一个角∠AOB，作出 ∠AOB的平分线OC. 在OC上任取一点P，过点P 画出OA，OB的垂线，分别记垂足为D，E，测量 PD，PE并作比较，你得到什么结论？在OC上再取几个点试一试. 通过以上测量，你发现了角的平分线的什么性质？
定理应用所具备的条件：
(2)点在该平分线上；
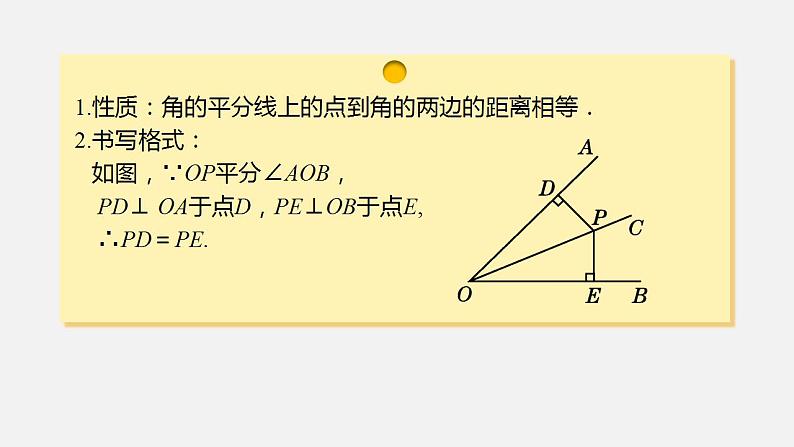
如图, ∠AOC=∠BOC，点 P 在OC 上，PD⊥OA,PE⊥QB，垂足分别为D，E.求证PD=PE.证明：∵PD⊥OA, PE⊥OB, ∴∠PDO=∠PEO=90°. 在△PDO和△PEO中， ∠PDO=∠PEO, ∠AOC=∠BOC, OP=OP, ∴△PDO ≌△PEO(AAS). ∴PD=PE.
如图，在△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于E，F在AC上，BE＝FC，求证：BD＝DF. 分析：要证BD＝DF，可考虑证两线段所在的△BDE和△FDC全等，两个三角形中已有一角和一边相等，只要再证DE＝CD即可，这可由AD平分∠CAB及垂直条件证得．
在△BDE和△FDC中，
∴ △BDE ≌ △FDC , ∴ BD=DF .
证明：∵AD平分∠CAB，DE⊥AB于E， ∠C＝90°，∴DE＝DC.
1.作∠AOB的平分线时，以O为圆心，某一长度为半径作弧，与OA，OB分别相交于C，D，然后分别以C，D为圆心，适当的长度为半径作弧，使两弧相交于一点，则这个适当的长度为(　　) A．大于 CD B．等于 CD C．小于 CD D．以上答案都不对
2.如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于E，若AB＝6 cm，则△DBE的周长是(　　)A．6 cm B．7 cm C．8 cm D．9 cm
3.如图，已知在△ABC中，CD是AB边上的高线， BE平分∠ABC，交CD于点E，BC＝50，DE＝14，则△BCE的面积等于________．