数学八年级上册第十三章 轴对称13.3 等腰三角形13.3.2 等边三角形课文ppt课件

这是一份数学八年级上册第十三章 轴对称13.3 等腰三角形13.3.2 等边三角形课文ppt课件，共19页。PPT课件主要包含了情景导入，合作探究，方法一从边看，当堂演练等内容，欢迎下载使用。
同学们知道等边三角形是特殊的等腰三角形，那么一个等腰三角形满足什么条件时，能使它成为等边三角形？把你的想法与同学们交流一下．
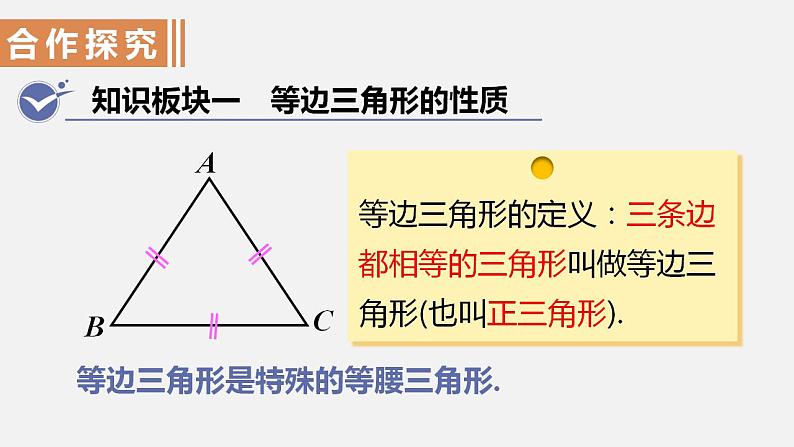
知识板块一　等边三角形的性质
等边三角形是特殊的等腰三角形.
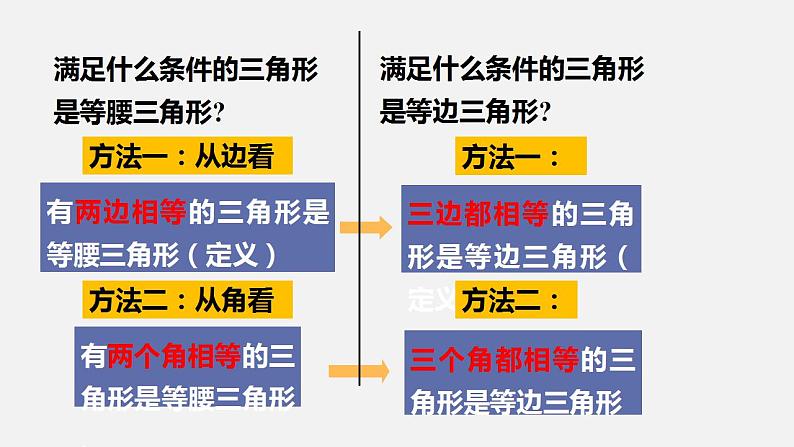
有两边相等的三角形是等腰三角形（定义）
有两个角相等的三角形是等腰三角形.
满足什么条件的三角形是等边三角形?
满足什么条件的三角形是等腰三角形?
三边都相等的三角形是等边三角形（定义）
三个角都相等的三角形是等边三角形
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”，你同意吗？
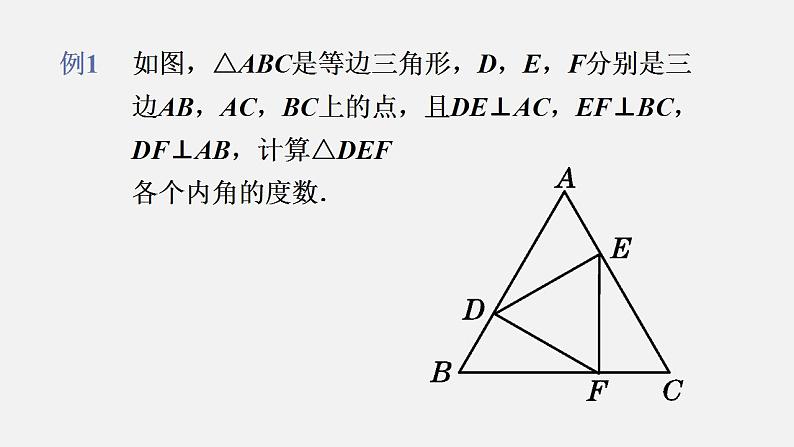
例1 如图，△ABC是等边三角形，D，E，F分别是三 边AB，AC，BC上的点，且DE⊥AC，EF⊥BC， DF⊥AB，计算△DEF 各个内角的度数．
分析：要计算出△DEF各个内角的度数，有两个途径， 即证△DEF为等边三角形或直接求各个角的度 数，由垂直定义及等边三角形的性质，显然直 接求各个角的度数较易．
解：因为△ABC是等边三角形， 所以∠A＝∠B＝∠C＝60°. 因为DE⊥AC，EF⊥BC，DF⊥AB， 所以∠AED＝∠EFC＝∠FDB＝90°， 所以∠ADE＝90°－∠A＝90°－60°＝30°， 所以∠EDF＝180°－30°－90°＝60°. 同理可得∠DEF＝∠EFD＝60°. 即△DEF各个内角的度数都是60°.
利用等边三角形的性质求角的度数时，通过利用等边三角形的三个内角都相等，并且每一个角都等于60°的性质，找出要求角与已知角间的关系来进行相关计算；有时还要结合全等图形等知识来解决．
知识板块二　等边三角形的判定
几何语言：∵AB=BC=AC∴△ABC是等边三角形
几何语言：∵ ∠A= ∠ B= ∠ C∴△ABC是等边三角形
几何语言：∵ ∠A=60°，AB=BC∴△ABC是等边三角形
例2 如图, △ABC是等边三角形, DE//BC,分别交 AB, AC于点D, E.求证: △ADE是等边三角形.证明：∵△ABC是等边三角形， ∴∠A=∠B=∠C. ∵DE//BC, ∴∠ADE=∠B, ∠AED=∠C. ∴∠A =∠ADE=∠AED. ∴△ADE是等边三角形.
1.如图，△ABC是等边三角形，点D在AC边上，∠DBC＝35°，则∠ADB的度数为(　　)A．25° B．60° C．85° D．95°
2.如图，△ABC是等边三角形，AD是角平分线，△ADE是等边三角形，下列结论：①AD⊥BC；②EF＝FD；③BE＝BD.其中正确结论的个数为(　　)A．3 B．2 C．1 D．0
3.如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于 点M，P，CD交BE于点Q，连接PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA＝60°；③△BPQ为等边三角形；④MB平分∠AMC，其中结论正确的有(　　)A．1个 B．2个 C．3个 D．4个
4.如图，已知△ABC是等边三角形，D为边 AC的中点，AE⊥EC，BD＝EC，证明：△ADE是等边三角形．
证明：∵△ABC是等边三角形，D为边AC的中点， ∴AB＝AC，∠BAC＝60°，BD⊥AC. ∵AE⊥EC，∴∠BDA＝∠CEA＝90°. 在Rt△ABD 和Rt△ACE中， AB＝AC， BD＝CE， ∴△ABD≌△ACE，∴AD＝AE，∠EAD＝∠BAD＝60°， ∴△ADE是等边三角形．