资料中包含下列文件,点击文件名可预览资料内容







还剩13页未读,
继续阅读
人教版22.1.1 二次函数优质课课件ppt
展开
这是一份人教版22.1.1 二次函数优质课课件ppt,文件包含2212二次函数yax2的图象和性质pptx、RJ中学数学九年级上册第二十二章二次函数2212二次函数y=ax²的图象和性质教学详案docx、同步练习docx等3份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
在类比探究二次函数y = ax 2 的图象和性质的过程中,进一步体会研究函数图象和性质的基本方法和数形结合的思想.
1.一次函数的图象是一条 .
3.二次函数的一般形式是什么?
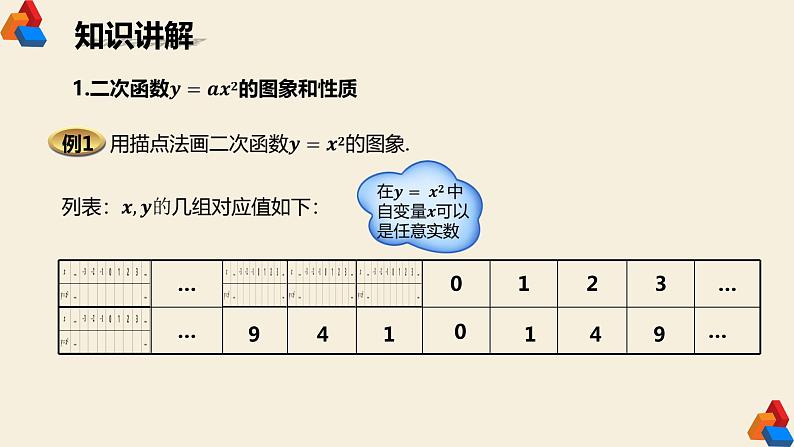
2.通常怎样画一个函数的图象?
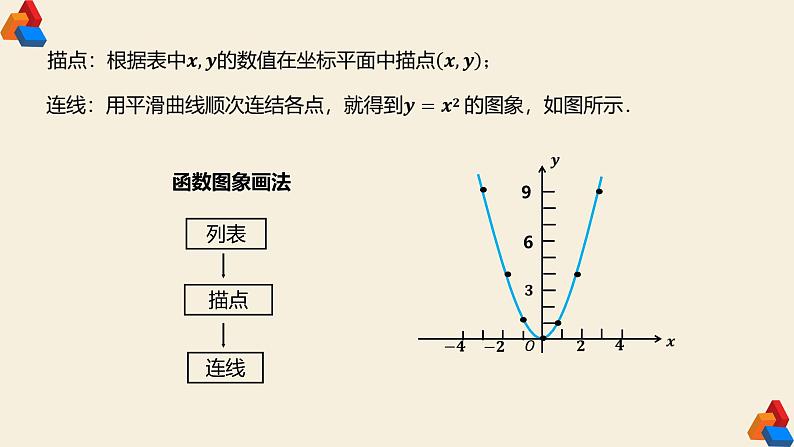
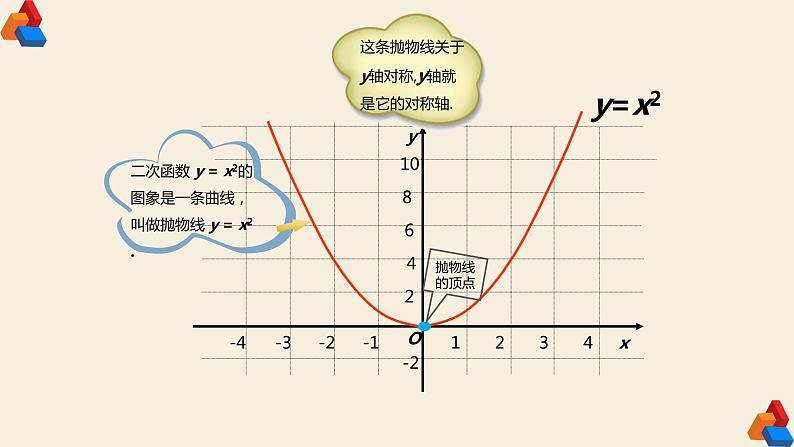
二次函数 y = x2的图象是一条曲线,叫做抛物线 y = x2 .
这条抛物线关于y轴对称,y轴就是它的对称轴.
顶点坐标是(0,0),是抛物线上的最低点.
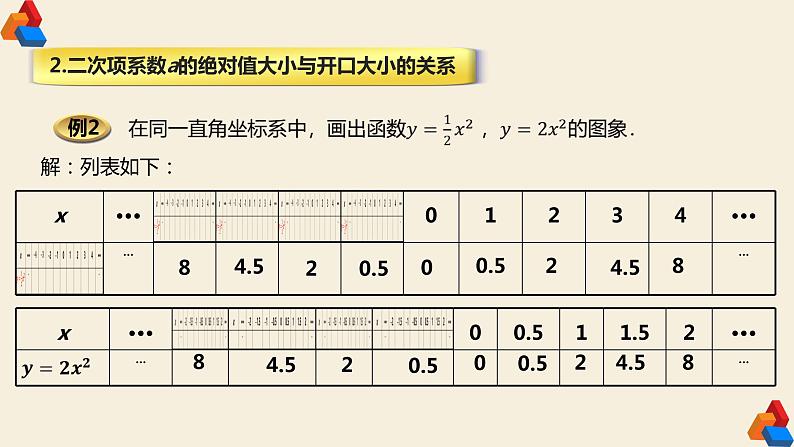
2.二次项系数a的绝对值大小与开口大小的关系
顶点坐标是(0,0),是抛物线上的最高点.
当a<0时,a的绝对值越大,开口越小.
a的绝对值越大,开口越小
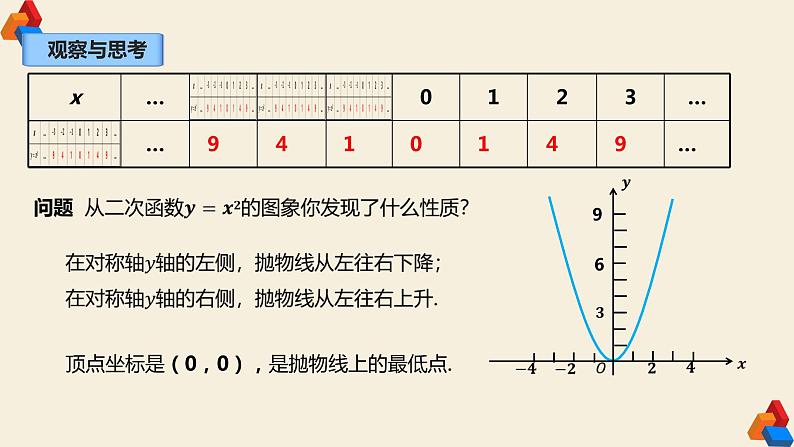
在对称轴左侧递减,在对称轴右侧递增
在对称轴左侧递增,在对称轴右侧递减
二次项系数互为相反数,开口相反,大小相同,它们关于x轴对称.
已知二次函数y=2x2. (1)若点(-2,y1)与(3,y2)在此二次函数的图象上,则y1_____y2;(填“>”“=”或“<”) (2)如图,此二次函数的图象经过点(0,0),长方形ABCD的顶点A、B在x轴上,C、D恰好在二次函数的图象上,若B点的横坐标为2,求图中阴影部分的面积之和.
(1)把两点的横坐标代入二次函数解析式得纵坐标
二次函数图象关于y轴对称
图象左边部分与右边部分对称
(2)两个阴影部分面积相加等于右边第一象限内的矩形面积
求不规则图形的面积,常采用等面积割补法,将不规则图形转化为规则图形以方便求解. 二次函数y=ax2的图象关于y轴对称,因此对称轴左右两侧折叠可以重合,因此比较二次函数的大小时,我们可以根据图象的对称性转变到同一变化区域中(全部为升或全部为降),根据图象中函数值高低去比较.
二次函数y=ax2的图象及性质
以对称轴为中心对称取点
在类比探究二次函数y = ax 2 的图象和性质的过程中,进一步体会研究函数图象和性质的基本方法和数形结合的思想.
1.一次函数的图象是一条 .
3.二次函数的一般形式是什么?
2.通常怎样画一个函数的图象?
二次函数 y = x2的图象是一条曲线,叫做抛物线 y = x2 .
这条抛物线关于y轴对称,y轴就是它的对称轴.
顶点坐标是(0,0),是抛物线上的最低点.
2.二次项系数a的绝对值大小与开口大小的关系
顶点坐标是(0,0),是抛物线上的最高点.
当a<0时,a的绝对值越大,开口越小.
a的绝对值越大,开口越小
在对称轴左侧递减,在对称轴右侧递增
在对称轴左侧递增,在对称轴右侧递减
二次项系数互为相反数,开口相反,大小相同,它们关于x轴对称.
已知二次函数y=2x2. (1)若点(-2,y1)与(3,y2)在此二次函数的图象上,则y1_____y2;(填“>”“=”或“<”) (2)如图,此二次函数的图象经过点(0,0),长方形ABCD的顶点A、B在x轴上,C、D恰好在二次函数的图象上,若B点的横坐标为2,求图中阴影部分的面积之和.
(1)把两点的横坐标代入二次函数解析式得纵坐标
二次函数图象关于y轴对称
图象左边部分与右边部分对称
(2)两个阴影部分面积相加等于右边第一象限内的矩形面积
求不规则图形的面积,常采用等面积割补法,将不规则图形转化为规则图形以方便求解. 二次函数y=ax2的图象关于y轴对称,因此对称轴左右两侧折叠可以重合,因此比较二次函数的大小时,我们可以根据图象的对称性转变到同一变化区域中(全部为升或全部为降),根据图象中函数值高低去比较.
二次函数y=ax2的图象及性质
以对称轴为中心对称取点













