2021-2022学年新疆兵团一中八年级（下）期末数学试卷（Word解析版）

这是一份2021-2022学年新疆兵团一中八年级（下）期末数学试卷（Word解析版），共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2021-2022学年新疆兵团一中八年级（下）期末数学试卷 题号一二三总分得分      一、选择题（本大题共8小题，共24分。在每小题列出的选项中，选出符合题目的一项）若在实数范围内有意义，则的取值范围是(    )A.  B.  C.  D. 下列等式成立的是(    )A.  B.
C.  D. 如图，平行四边形中，平分，，则等于(    )
 A.  B.  C.  D. 下列各组数中，不能作直角三角形三边长的是(    )A. ，， B. ，， C. ，， D. ，，若实数，满足，则的值是(    )A.  B.  C.  D. 如图，四边形的对角线，交于点，则不能判断四边形是平行四边形的是(    )
 A. ， B. ，
C. ， D. ，如图，在中，，，以，为边作正方形，这两个正方形的面积和为(    )A.
B.
C.
D.
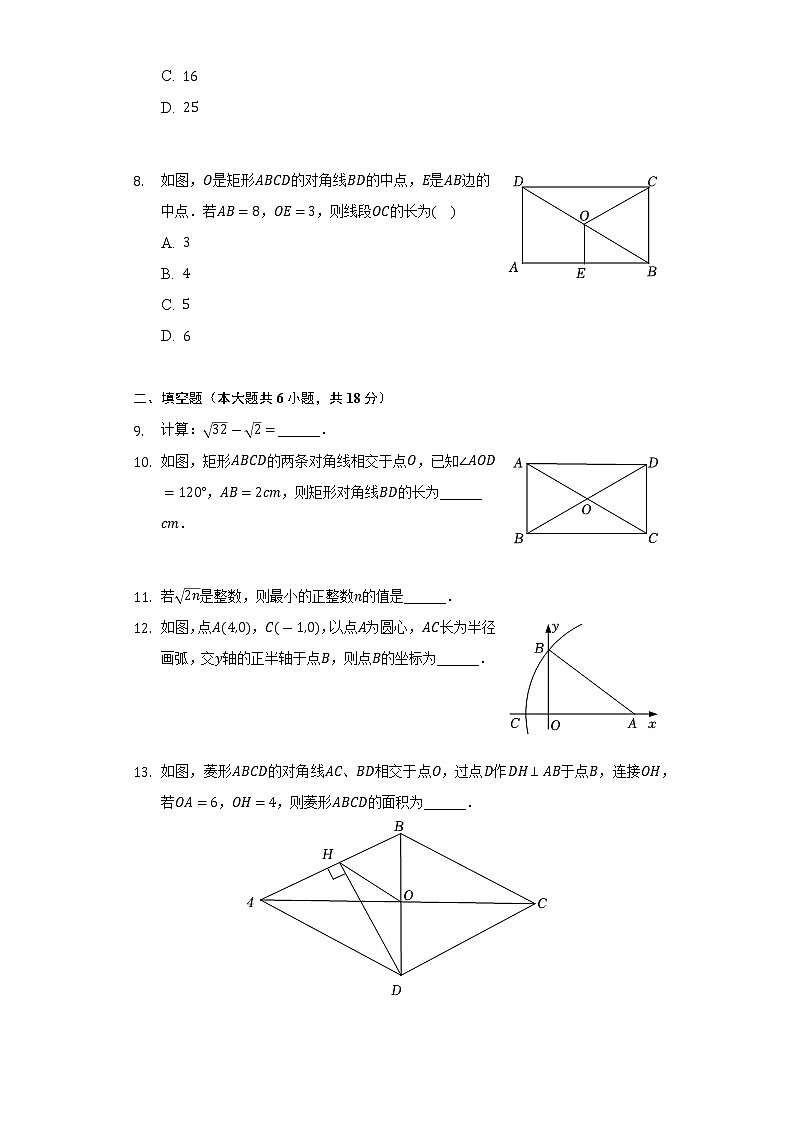
 如图，是矩形的对角线的中点，是边的中点．若，，则线段的长为(    )A.
B.
C.
D.  二、填空题（本大题共6小题，共18分）计算：______．如图，矩形的两条对角线相交于点，已知，，则矩形对角线的长为______．
 若是整数，则最小的正整数的值是______．如图，点，，以点为圆心，长为半径画弧，交轴的正半轴于点，则点的坐标为______．
 如图，菱形的对角线、相交于点，过点作于点，连接，若，，则菱形的面积为______．
如图，正方形的边长为，点，分别在边，上，若是的中点，且，则的长为______
   三、解答题（本大题共8小题，共58分。解答应写出文字说明，证明过程或演算步骤）本小题分
计算：
；
．本小题分
已知，，分别求下列代数式的值：
；
．本小题分
如图，在平行四边形中，对角线、相交于点，过作直线分别交、于、两点，求证：．
本小题分
已知矩形的长为，宽为且，．
求矩形的周长；
当时，求正方形的边长的值．注：表示面积本小题分
如图，学校操场边上一块空地阴影部分需要绿化，连接，测出，，，，，求需要绿化部分的面积．
本小题分
已知：如图，在▱中，点是的中点，连接并延长交的延长线于点，连接．
求证：≌；
若，判断四边形的形状，并说明理由．
本小题分
如图，在正方形中，对角线，相交于点，点，是对角线上的两点，且连接，，，．
证明：≌．
若，，求四边形的周长．
本小题分
如图，中，，，，点从点出发沿方向以秒的速度向点匀速运动，同时点从点出发沿方向以秒的速度向点匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点、运动的时间是秒过点作于点，连接、．
求证：；
四边形能够成为菱形吗？如果能，求出相应的值；如果不能，请说明理由；
当为何值时，为直角三角形？请说明理由．

答案和解析 1.【答案】 【解析】解：由题意可得，
解得：，
故选：．
根据二次根式有意义的条件列不等式组求解．
本题考查二次根式有意义的条件，理解二次根式有意义的条件被开方数为非负数是解题关键．
 2.【答案】 【解析】解：原式，故A错误；
原式，故B错误；
原式，故C错误；
故选：．
根据二次根式的运算法则即可求出答案．
本题考查二次根式，解题的关键是熟练运用二次根式的运算，本题属于基础题型．
 3.【答案】 【解析】【分析】
本题考查了平行四边形的性质，并利用了两直线平行，同旁内角互补和角的平分线的性质．根据平行四边形的性质和角平分线的定义求解．
【解答】
解：在▱中，
，
．
平分，
．
，
．
故选D．  4.【答案】 【解析】解：，，
，
以，，为边不能组成直角三角形，故本选项符合题意；
B.，，
，
以，，为边能组成直角三角形，故本选项不符合题意；
C.，，
，
以，，为边能组成直角三角形，故本选项不符合题意；
D.，，
，
以，，为边能组成直角三角形，故本选项不符合题意；
故选：．
先分别求出两小边的平方和和最长边的平方，再看看是否相等即可．
本题考查了勾股定理的逆定理，能熟记勾股定理的逆定理是解此题的关键，注意：如果一个三角形的两边、的平方和等于第三边的平方，那么这个三角形是直角三角形．
 5.【答案】 【解析】解：，，
，，
，
，
，
故选：．
根据二次根式有意义的条件，求出，代入关系式中求出，从而得到的值．
本题考查了二次根式有意义的条件，掌握二次根式有意义的条件是被开方数是非负数是解题的关键．
 6.【答案】 【解析】解：、，，四边形是平行四边形，故此选项不合题意；
B、，，不能判断四边形是平行四边形，故此选项符合题意；
C、，，四边形是平行四边形，故此选项不合题意；
D、，，四边形是平行四边形，故此选项不合题意；
故选：．
利用所给条件结合平行四边形的判定方法进行分析即可．
此题主要考查了平行四边形的判定，关键是掌握两组对边分别平行的四边形是平行四边形．两组对边分别相等的四边形是平行四边形．一组对边平行且相等的四边形是平行四边形．两组对角分别相等的四边形是平行四边形．对角线互相平分的四边形是平行四边形．
 7.【答案】 【解析】解：为直角三角形，
阴影部分的面积和为．
故选：．
根据勾股定理得出这两个正方形的面积和等于的平方解答即可．
此题考查勾股定理，关键是根据这两个正方形的面积和等于的平方解答．
 8.【答案】 【解析】解：四边形是矩形，
，，
是边的中点，
是的中位线，
，
，
，
，
故选：．
根据矩形的性质和三角形中位线定理得出，进而利用勾股定理得出，再根据直角三角形的性质解答即可．
此题考查矩形的性质，关键是根据矩形的性质和三角形中位线定理得出解答．
 9.【答案】 【解析】解：原式．
故答案为：．
先将二次根式化为最简，然后合并同类二次根式即可得出答案．
此题考查了二次根式的加减运算，属于基础题，掌握二次根式的化简及同类二次根式的合并是关键．
 10.【答案】 【解析】解：四边形是矩形，
，，
，
，
是等边三角形，
，
，
，
故答案为：．
由可知，而矩形的对角线平分且相等得，所以是等边三角形，所以，故BD．
本题考查了矩形的性质和等边三角形的判定，关键是结合图形求出是等边三角形，进而求解．
 11.【答案】 【解析】解：是整数，是正整数，
最小的值是，
最小的正整数的值是．
故答案为：．
若是整数，是正整数，则最小的值是，故．
此题主要考查了二次根式的定义，根据二次根式的性质正确化简二次根式是解题关键．
 12.【答案】 【解析】解：，
，

在中，．
．
故答案为：．
根据已知可得，利用勾股定理即可求解．
本题考查勾股定理的应用、坐标的特征知识．关键在于利用点的坐标表示边的长度．
 13.【答案】 【解析】解：四边形是菱形，
，，，
，
，
，
，
菱形的面积，
故答案为：．
由菱形的性质得，，，则，再由直角三角形斜边上的中线性质求出的长度，然后由菱形的面积公式求解即可．
本题主要考查了菱形的性质，直角三角形的斜边上的中线性质，菱形的面积公式等知识；熟练掌握菱形的性质，求出的长是解题的关键．
 14.【答案】 【解析】解：延长至，使，连接、，如图所示：
四边形是正方形，
，，
，
在和中，，
≌，
，，
，
，
，
在和中，，
≌，
，
是的中点，
，
设，则，
在中，由勾股定理得：，
解得：，即，
，
故答案为：．
延长至，使，连接，由证明≌，得出，，再证明≌，得出，设，则，在中，由勾股定理得出方程，解方程得出，从而求得的长即可．
此题考查了正方形的性质，全等三角形的判定与性质以及勾股定理，利用了方程的思想，证明三角形全等是解本题的关键．
 15.【答案】解：

；


． 【解析】先化简，再算加减运算即可；
先算二次根式的乘法，绝对值，零指数幂，再算加减即可．
本题主要考查二次根式的混合运算，解答的关键是对相应的运算法则的掌握．
 16.【答案】解：，，
，，
；
． 【解析】根据二次根式的加法法则、减法法则分别求出，，再根据平方差公式计算；
根据完全平方公式计算．
本题考查的是二次根式的化简求值，掌握完全平方公式、平方差公式是解题的关键．
 17.【答案】证明：在平行四边形中，，，
，
在与中，
，
，
． 【解析】根据平行四边形的性质可得，，证明即可得结论．
本题考查了平行四边形的性质，全等三角形的判定，解决本题的关键是掌握平行四边形的性质．
 18.【答案】解：矩形的长为，宽为且，．
矩形的周长；

设正方形的边长为，则．
，
，
负值舍去，
正方形的周长． 【解析】根据矩形的周长长宽，列式计算即可；
设正方形的边长为，根据，列出方程，解方程求出，进而求出正方形的周长．
本题考查了二次根式的应用，掌握矩形、正方形的周长与面积公式是解题的关键．
 19.【答案】解：在直角中，，，则由勾股定理知：．
在中，，，，
，，
，
，
需要绿化部分的面积，
答：需要绿化部分的面积为． 【解析】根据勾股定理的逆定理得到，根据三角形的面积公式计算，即可得到答案．
本题考查的是勾股定理和勾股定理的逆定理的应用，三角形的面积计算，掌握勾股定理、勾股定理的逆定理是解决问题的关键．
 20.【答案】证明：如图．
四边形是平行四边形，
即，
，
点是的中点，
．
在和中，
，
≌．
解：四边形是矩形．理由如下：
≌，
，
，
四边形是平行四边形，
，
，
，
四边形是矩形． 【解析】根据平行四边形性质得出，推出，根据证两三角形全等即可；
根据全等得出，根据得出平行四边形，推出，根据矩形的判定推出即可．
本题考查了平行四边形的性质和判定，矩形的判定，全等三角形的性质和判定等知识点的应用，熟练掌握基本图形的性质是解题的关键．
 21.【答案】解；证明：由正方形对角线平分每一组对角可知：，
在和中，
，
≌．
，
，
由正方形对角线相等且互相垂直平分可得：，，，
又，
，
即，
故四边形为菱形．
，
．

故四边形的周长为． 【解析】由正方形对角线性质可得，再由可证≌；
由正方形性质及勾股定理可求得，再证明四边形为菱形，因为，所以可得，在中用勾股定理求得，进而四边形的周长为，即可求得答案．
本题考查了全等三角形的判定，菱形的判定与性质，勾股定理，正方形的性质，熟悉以上几何图形的性质和判定是解题关键．
 22.【答案】证明：中，．
，，
又在中，，
，
；

解：，，
四边形是平行四边形，
当时，四边形是菱形，
即，
解得：，
即当时，▱是菱形；

当时，是直角三角形；
当时，是直角三角形理由如下：
当时，．

，
，
，
，
时，．
当时，，
四边形是平行四边形，
，
，
是直角三角形，，
，
，
，
，，
，
解得．
当时，点和点都和点重合，不能构成三角形，所以，此种情况不存在；
综上所述，当时，是直角三角形；当时，是直角三角形． 【解析】利用表示出以及的长，然后在直角中，利用直角三角形的性质求得的长，即可证明；
易证四边形是平行四边形，当时，四边形是菱形，据此即可列方程求得的值；
分三种情况，建立方程求解即可．
此题是四边形综合题，主要考查了直角三角形的性质，菱形的性质，解本题的关键是用分类讨论的思想解决问题．