2022年中考数学真题分类汇编：反比例函数2(含答案)

这是一份2022年中考数学真题分类汇编：反比例函数2(含答案)，共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022年中考数学真题汇编反比例函数
一、选择题
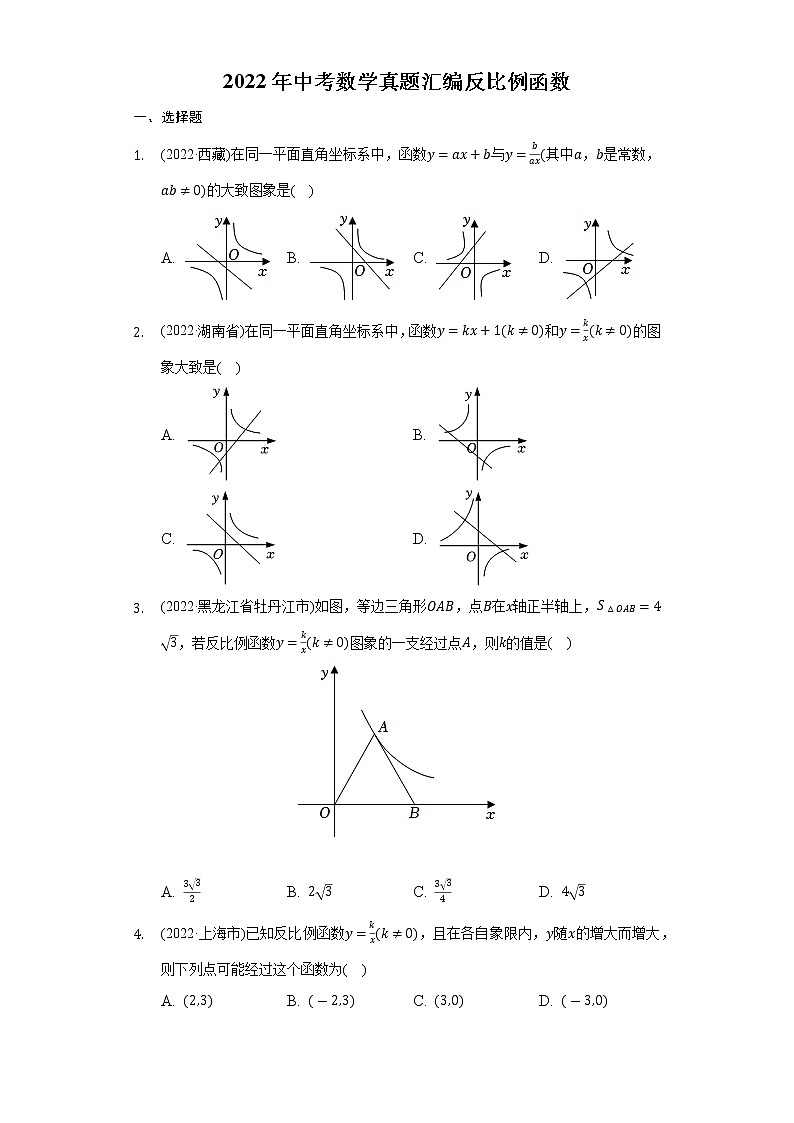
1. (2022·西藏)在同一平面直角坐标系中，函数y=ax+b与y=bax(其中a，b是常数，ab≠0)的大致图象是(    )
A. B. C. D.
2. (2022·湖南省)在同一平面直角坐标系中，函数y=kx+1(k≠0)和y=kx(k≠0)的图象大致是(    )
A. B.
C. D.
3. (2022·黑龙江省牡丹江市)如图，等边三角形OAB，点B在x轴正半轴上，S△OAB=43，若反比例函数y=kx(k≠0)图象的一支经过点A，则k的值是(    )

A. 332 B. 23 C. 334 D. 43
4. (2022·上海市)已知反比例函数y=kx(k≠0)，且在各自象限内，y随x的增大而增大，则下列点可能经过这个函数为(    )
A. (2,3) B. (-2,3) C. (3,0) D. (-3,0)
5. (2022·吉林省长春市)如图，在平面直角坐标系中，点P在反比例函数y=kx(k>0,x>0)的图象上，其纵坐标为2，过点P作PQ/​/y轴，交x轴于点Q，将线段QP绕点Q顺时针旋转60°得到线段QM.若点M也在该反比例函数的图像上，则k的值为(    )


A. 32 B. 3 C. 23 D. 4
6. (2022·内蒙古自治区通辽市)如图，点D是▱OABC内一点，AD与x轴平行，BD与y轴平行，BD=3，∠BDC=120°，S△BCD=923，若反比例函数y=kx(x<0)的图像经过C，D两点，则k的值是(    )

A. -63 B. -6 C. -123 D. -12
7. (2022·湖南省郴州市)如图，在函数y=2x(x>0)的图象上任取一点A，过点A作y轴的垂线交函数y=-8x(x<0)的图象于点B，连接OA，OB，则△AOB的面积是(    )

A. 3 B. 5 C. 6 D. 10
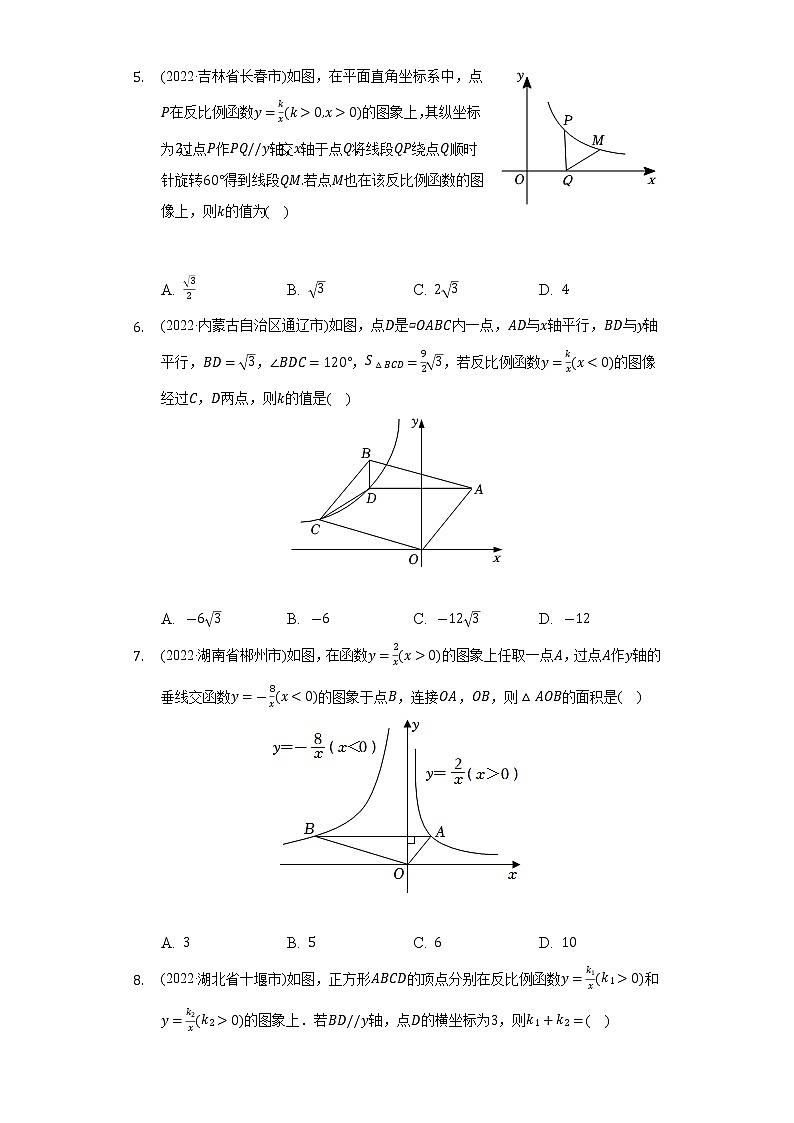
8. (2022·湖北省十堰市)如图，正方形ABCD的顶点分别在反比例函数y=k1x(k1>0)和y=k2x(k2>0)的图象上．若BD/​/y轴，点D的横坐标为3，则k1+k2=(    )

A. 36 B. 18 C. 12 D. 9
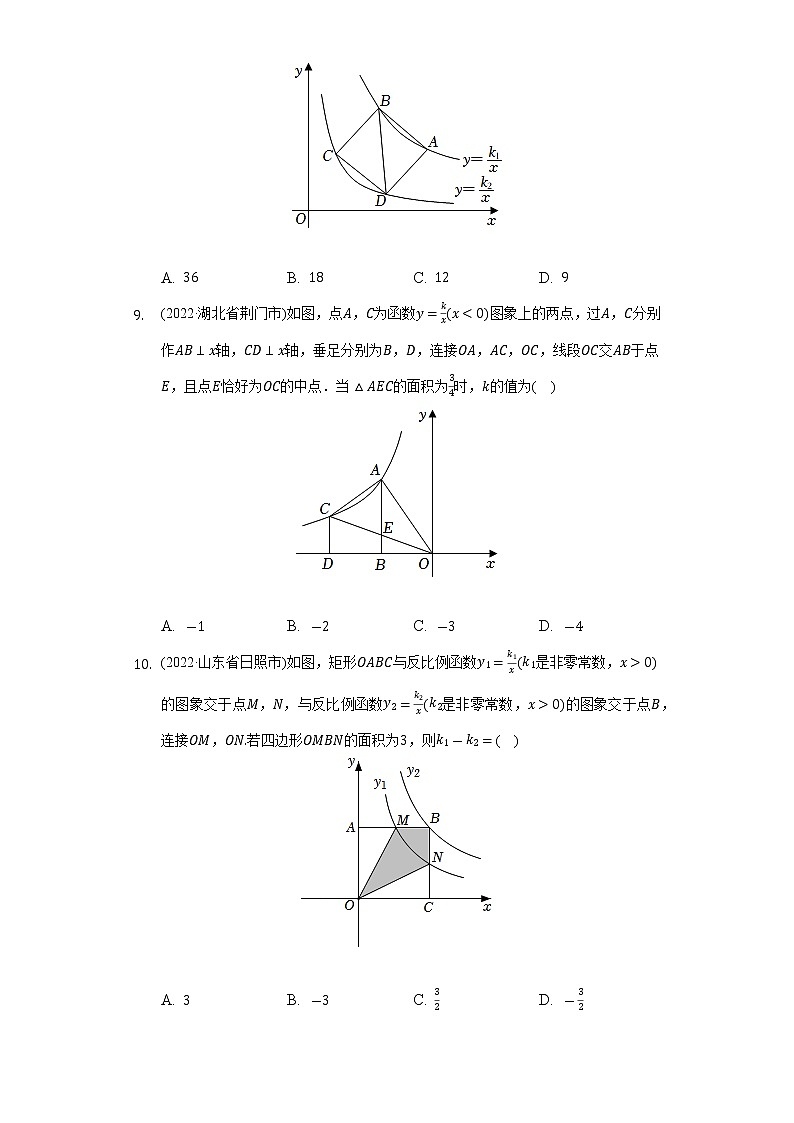
9. (2022·湖北省荆门市)如图，点A，C为函数y=kx(x<0)图象上的两点，过A，C分别作AB⊥x轴，CD⊥x轴，垂足分别为B，D，连接OA，AC，OC，线段OC交AB于点E，且点E恰好为OC的中点．当△AEC的面积为34时，k的值为(    )

A. -1 B. -2 C. -3 D. -4
10. (2022·山东省日照市)如图，矩形OABC与反比例函数y1=k1x(k1是非零常数，x>0)的图象交于点M，N，与反比例函数y2=k2x(k2是非零常数，x>0)的图象交于点B，连接OM，ON.若四边形OMBN的面积为3，则k1-k2=(    )

A. 3 B. -3 C. 32 D. -32
11. (2022·贵州省贵阳市)如图，在平面直角坐标系中有P，Q，M，N四个点，其中恰有三点在反比例函数y=kx(k>0)的图象上．根据图中四点的位置，判断这四个点中不在函数y=kx的图象上的点是(    )
A. 点P
B. 点Q
C. 点M
D. 点N
12. (2022·海南省)若反比例函数y=kx(k≠0)的图象经过点(2,-3)，则它的图象也一定经过的点是(    )
A. (-2,-3) B. (-3,-2) C. (1,-6) D. (6,1)
13. (2022·江苏省泰州市)已知点(-3,y1)、(-1,y2)、(1,y3)在下列某一函数图像上，且y3 A. y=3x B. y=3x2 C. y=3x D. y=-3x
14. (2022·贵州省黔东南苗族侗族自治州)若二次函数y=ax2+bx+c(a≠0)的图象如图所示，则一次函数y=ax+b与反比例函数y=-cx在同一坐标系内的大致图象为(    )

A. B.





C. D.







15. (2022·广西壮族自治区贺州市)已知一次函数y=kx+b的图象如图所示，则y=-kx+b与y=bx的图象为(    )
A.
B.
C.
D.
二、填空题
16. (2022·湖南省益阳市)反比例函数y=k-2x的图象分布情况如图所示，则k的值可以是______(写出一个符合条件的k值即可)．











17. (2022·山东省济宁市)如图，A是双曲线y=8x(x>0)上的一点，点C是OA的中点，过点C作y轴的垂线，垂足为D，交双曲线于点B，则△ABD的面积是______．

18. (2022·江苏省盐城市)已知反比例函数的图象经过点(2,3)，则该函数表达式为______．
19. (2022·青海省)如图，一块砖的A，B，C三个面的面积之比是5：3：1.如果A，B，C三个面分别向下在地上，地面所受压强分别为P1，P2，P3，压强的计算公式为P=FS，其中P是压强，F是压力，S是受力面积，则P1，P2，P3的大小关系为______(用小于号连接)．


20. (2022·广西壮族自治区河池市)如图，点P(x,y)在双曲线y=kx的图象上，PA⊥x轴，垂足为A，若S△AOP=2，则该反比例函数的解析式为______．


21. (2022·湖南省郴州市)科技小组为了验证某电路的电压U(V)、电流I(A)、电阻R(Ω)三者之间的关系：I=UR，测得数据如下：
R(Ω)
100
200
220
400
I(A)
2.2
1.1
1
0.55
那么，当电阻R=55Ω时，电流I=______A.



22. (2022·广东省深圳市)如图，已知直角三角形ABO中，AO=1，将△ABO绕O点旋转至△A'B'O的位置，且A'在OB中点，B'在反比例函数y=kx上，则k的值______．

23. (2022·山东省烟台市)如图，A，B是双曲线y=kx(x>0)上的两点，连接OA，OB.过点A作AC⊥x轴于点C，交OB于点D.若D为AC的中点，△AOD的面积为3，点B的坐标为(m,2)，则m的值为______．

24. (2022·贵州省铜仁市)如图，点A、B在反比例函数y=kx的图象上，AC⊥y轴，垂足为D，BC⊥AC.若四边形AOBC间面积为6，ADAC=12，则k的值为______．


25. (2022·辽宁省铁岭市)如图，矩形OABC的顶点B在反比例函数y=kx(x>0)的图象上，点A在x轴的正半轴上，AB=3BC，点D在x轴的负半轴上，AD=AB，连接BD，过点A作AE/​/BD交y交于点E，点F在AE上，连接FD，FB.若△BDF的面积为9，则k的值是______．



三、解答题
26. (2022·青海省西宁市)如图，正比例函数y=4x与反比例函数y=kx(x>0)的图象交于点A(a,4)，点B在反比例函数图象上，连接AB，过点B作BC⊥x轴于点C(2,0)．
(1)求反比例函数解析式；
(2)点D在第一象限，且以A，B，C，D为顶点的四边形是平行四边形，请直接写出点D的坐标．

27. (2022·湖南省湘西土家族苗族自治州)如图，一次函数y=ax+1(a≠0)的图象与x轴交于点A，与反比例函数y=kx的图象在第一象限交于点B(1,3)，过点B作BC⊥x轴于点C．
(1)求一次函数和反比例函数的解析式．
(2)求△ABC的面积．










28. (2022·辽宁省盘锦市)如图，平面直角坐标系xOy中，四边形OABC是菱形，点A在y轴正半轴上，点B的坐标是(-4,8)，反比例函数y=kx(x<0)的图象经过点C．
(1)求反比例函数的解析式；
(2)点D在边CO上，且CDDO=34，过点D作DE/​/x轴，交反比例函数的图象于点E，求点E的坐标．

29. (2022·甘肃省兰州市)如图，点A在反比例函数y=kx(x>0)的图象上，AB⊥x轴，垂足为B(3,0)，过C(5,0)作CD⊥x轴，交过B点的一次函数y=32x+b的图象于D点，交反比例函数的图象于E点，S△AOB=3．
(1)求反比例比数y=kx(x>0)和一次函数y=32x+b的表达式；
(2)求DE的长．





30. (2022·辽宁省大连市)密闭容器内有一定质量的二氧化碳，当容器的体积V(单位：m3)变化时，气体的密度ρ(单位：kg/m3)随之变化．已知密度ρ与体积V是反比例函数关系，它的图象如图所示，当V=5m3时，ρ=1.98kg/m3．
(1)求密度ρ关于体积V的函数解析式；
(2)若3≤V≤9，求二氧化碳密度ρ的变化范围．

31. (2022·广西壮族自治区柳州市)如图，在平面直角坐标系中，一次函数y=k1x+b(k1≠0)的图象与反比例函数y=k2x(k2≠0)的图象相交于A(3,4)，B(-4,m)两点．
(1)求一次函数和反比例函数的解析式；
(2)若点D在x轴上，位于原点右侧，且OA=OD，求△AOD的面积．

32. (2022·上海市)一个一次函数的截距为-1，且经过点A(2,3)．
(1)求这个一次函数的解析式；
(2)点A，B在某个反比例函数上，点B横坐标为6，将点B向上平移2个单位得到点C，求cos∠ABC的值．




33. (2022·广西壮族自治区贵港市)如图，直线AB与反比例函数y=kx(k>0,x>0)的图象相交于点A和点C(3,2)，与x轴的正半轴相交于点B．
(1)求k的值；
(2)连接OA，OC，若点C为线段AB的中点，求△AOC的面积．

34. (2022·山东省聊城市)如图，直线y=px+3(p≠0)与反比例函数y=kx(k>0)在第一象限内的图象交于点A(2,q)，与y轴交于点B，过双曲线上的一点C作x轴的垂线，垂足为点D，交直线y=px+3于点E，且S△AOB：S△COD=3：4．
(1)求k，p的值；
(2)若OE将四边形BOCE分成两个面积相等的三角形，求点C的坐标．







35. (2022·辽宁省营口市)如图，在平面直角坐标系中，△OAC的边OC在y轴上，反比例函数y=kx(x>0)的图象经过点A和点B(2,6)，且点B为AC的中点．
(1)求k的值和点C的坐标；
(2)求△OAC的周长．


参考答案
1.解：若a>0，b>0，
则y=ax+b经过一、二、三象限，反比例函数y=bax(ab≠0)位于一、三象限，
若a>0，b<0，
则y=ax+b经过一、三、四象限，反比例函数数y=bax(ab≠0)位于二、四象限，
若a<0，b>0，
则y=ax+b经过一、二、四象限，反比例函数y=bax(ab≠0)位于二、四象限，
若a<0，b<0，
则y=ax+b经过二、三、四象限，反比例函数y=bax(ab≠0)位于一、三象限，
故选：A．
根据a、b的取值，分别判断出两个函数图象所过的象限，要注意分类讨论．
本题主要考查了一次函数和反比例函数的图象，熟知一次函数、反比例函数的性质是解题的关键．

2.解：当k>0时，一次函数y=kx+1经过第一、二、三象限，反比例函数y=kx位于第一、三象限；
当k<0时，一次函数y=kx+1经过第一、二、四象限，反比例函数y=kx位于第二、四象限；
故选：D．
分k>0或k<0，根据一次函数与反比例函数的性质即可得出答案．
本题主要考查了反比例函数和一次函数的图象与性质，熟练掌握k>0，图象经过第一、三象限，k<0，图象经过第二、四象限是解题的关键．

3.解：如图，过点A作AC⊥OB于点C，
∵△OAB是正三角形，
∴OC=BC，
∴S△AOC=12S△AOB=23=12|k|，
又∵k>0，
∴k=43，
故选：D．
根据正三角形的性质以及反比例函数系数k的几何意义，得出S△AOC=12S△AOB=23=12|k|，即可求出k的值．
本题考查等边三角形的性质，反比例函数系数k的几何意义，掌握等边三角形的性质以及反比例函数系数k的几何意义是正确解答的前提．

4.解：因为反比例函数y=kx(k≠0)，且在各自象限内，y随x的增大而增大，
所以k<0，
A.2×3=6>0，故本选项不符合题意；
B.-2×3=-6<0，故本选项符合题意；
C.3×0=0，故本选项不符合题意；
D.-3×0=0，故本选项不符合题意；
故选：B．
根据反比例函数的性质判断即可．
本题主要考查反比例函数的性质：当k>0时，在每一个象限内，y随x的增大而减小；当k<0时，在每一个象限，y随x的增大而增大．

5.解：作MN⊥x轴于N，
∵P在反比例函数y=kx(k>0,x>0)的图象上，其纵坐标为2，过点P作PQ/​/y轴，交x轴于点Q，
∴P(k2,2)，
∴PQ=2，
∵将线段QP绕点Q顺时针旋转60°得到线段QM．
∴QM=QP=2，∠POM=60°，
∴∠MQN=90°-60°=30°，
∴MN=12QM=1，
∴QN=22-12=3，
∴M(k2+3,1)，
∵点M也在该反比例函数的图象上，
∴k=k2+3，
解得k=23，
故选：C．
作MN⊥x轴于N，根据题意P(k2,2)，PQ=2，由于将线段QP绕点Q顺时针旋转60°得到线段QM，得出QM=QP=2，∠POM=60°，即可得出∠MQN=30°，即可得出MN=12QM=1，QN=22-12=3，得到M(k2+3,1)，代入反比例函数解析式即可求得k的值．
本题考查了反比例函数图象上点的坐标特征，坐标与图形变化-旋转，表示出M点的坐标是解题的关键．

6.解：过点C作CE⊥y轴，延长BD交CE于点F，
∵四边形OABC为平行四边形，
∴AB/​/OC，AB=OC，
∴∠COE=∠ABD，
∵BD与y轴平行，
∴∠ADB=90°，
在△COE和△ABD中，
∠ADB=∠CEO∠COE=∠ABDOC=AB，
∴△COE≌△ABD(AAS)，
∴OE=BD=3，
∵S△BDC=12BD⋅CF=923，
∴CF=9，
∵∠BDC=120°，
∴∠CDF=60°，
∴DF=33，
点D的纵坐标为43，
设C(m,3)，则D(m+9,43)，
∵反比例函数y=kx(x<0)的图象经过C，D两点，
∴k=3m=43(m+9)，
∴m=-12，
∴k=-123，
故选：C．
过点C作CE⊥y轴，延长BD交CE于点F，易证△COE≌△ABD，求得OE=3，根据S△BCD=923，求得CF=9，得到点D的纵坐标为43，设C(m,3)，则D(m+9,43)，由反比例函数y=kx(x<0)的图象经过C，D两点，从而求出m，进而可得k的值．
本题主要考查反比例函数，掌握平行四边形的性质和反比例函数图象的坐标特征是解题的关键．

7.解：∵点A在函数y=2x(x>0)的图象上，
∴S△AOC=12×2=1，
又∵点B在反比例函数y=-8x(x<0)的图象上，
∴S△BOC=12×8=4，
∴S△AOB=S△AOC+S△BOC
=1+5
=5，
故选：B．
根据反比例函数系数k的几何意义进行计算即可．
本题考查反比例函数系数k的几何意义，理解反比例函数系数k的几何意义是正确解答的关键．

8.解：连接AC交BD于E，延长BD交x轴于F，连接OD、OB，如图：

∵四边形ABCD是正方形，
∴AE=BE=CE=DE，
设AE=BE=CE=DE=m，D(3,a)，
∵BD/​/y轴，
∴B(3,a+2m)，A(3+m,a+m)，
∵A，B都在反比例函数y=k1x(k1>0)的图象上，
∴k1=3(a+2m)=(3+m)(a+m)，
∵m≠0，
∴m=3-a，
∴B(3,6-a)，
∵B(3,6-a)在反比例函数y=k1x(k1>0)的图象上，D(3,a)在y=k2x(k2>0)的图象上，
∴k1=3(6-a)=18-3a，k2=3a，
∴k1+k2=18-3a+3a=18；
故选：B．
连接AC交BD于E，延长BD交x轴于F，连接OD、OB，设AE=BE=CE=DE=m，D(3,a)，根据BD/​/y轴，可得B(3,a+2m)，A(3+m,a+m)，即知k1=3(a+2m)=(3+m)(a+m)，从而m=3-a，B(3,6-a)，由B(3,6-a)在反比例函数y=k1x(k1>0)的图象上，D(3,a)在y=k2x(k2>0)的图象上，得k1=3(6-a)=18-3a，k2=3a，即得k1+k2=18-3a+3a=18．
本题考查反比例函数及应用，涉及正方形性质，解题的关键是用含字母的代数式表示相关点坐标．

9.解：∵点E为OC的中点，
∴△AEO的面积=△AEC的面积=34，
∵点A，C为函数y=kx(x<0)图象上的两点，
∴S△ABO=S△CDO，
∴S四边形CDBE=S△AEO=34，
∵EB//CD，
∴△OEB∽△OCD，
∴S△OEBS△OCD=(12)2，
∴S△OCD=1，
则12xy=-1，
∴k=xy=-2．
故选：B．
根据三角形的中线的性质求出△AEO的面积，根据相似三角形的性质求出S△OCD=1，根据反比例函数系数k的几何意义解答即可．
本题考查的是反比例函数系数k的几何意义、相似三角形的性质，掌握反比例函数系数k的几何意义、相似三角形的面积比等于相似比的平方是解题的关键．

10.解：∵点M、N均是反比例函数y1=k1x(k1是非零常数，x>0)的图象上，
∴S△OAM=S△OCN=12k1，
∵矩形OABC的顶点B在反比例函数y2=k2x(k2是非零常数，x>0)的图象上，
∴S矩形OABC=k2，
∴S矩形OMBN=S矩形OABC-S△OAM-S△OCN=3，
∴k2-k1=3，
∴k1-k2=-3，
故选：B．
根据矩形的性质以及反比例函数系数k的几何意义即可得出结论．
本题考查了矩形的性质，反比例函数系数k的几何意义：在反比例函数y=kx图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．

11.解：如图，反比例函数y=kx的图象是双曲线，若点在反比例函数的图象上，则其纵横坐标的积为常数k，即xy=k，
通过观察发现，点P、Q、N可能在图象上，点M不在图象上，
故选：C．
根据反比例函数图象上点的坐标特征以及反比例函数的图象进行判断即可．
本题考查反比例函数图象上点的坐标特征，掌握反比例函数的图象以及图象上点的坐标特征是正确判断的前提．

12.解：∵反比例函数y=kx(k≠0)的图象经过点(2,-3)，
∴k=2×(-3)=-6，
A、-2×(-3)=6≠-6，故A不正确，不符合题意；
B、(-3)×(-2)=6≠-6，故B不正确，不符合题意；
C、1×(-6)=-6，故C正确，符合题意，
D、6×1=6≠-6，故D不正确，不符合题意．
故选：C．
将(2,-3)代入y=kx(k≠0)即可求出k的值，再根据k=xy解答即可．
本题主要考查反比例函数图象上点的坐标特征，所有在反比例函数上的点的横纵坐标的积应等于比例系数．

13.解：A.y=3x，因为3>0，所以y随x的增大而增大，所以y1 B.y=3x2，当x=1和x=-1时，y相等，即y3=y2，故不符合题意；
C.y=3x，当x<0时，y随x的增大而减小，x>0时，y随x的增大而减小，所以y2 D.y=-3x，当x<0时，y随x的增大而增大，x>0时，y随x的增大而增大，所以y3 故选：D．
根据所学知识可判断每个选项中对应的函数的增减性，进而判断y3，y1，y2之间的关系，再判断即可．
本题主要考查一次函数的性质，反比例函数的性质及二次函数的性质，掌握相关函数的性质是解题关键，也可直接代入各个选项中的函数解析中，再判断y的大小．

14.解：∵抛物线开口向上，
∴a>0，
∵抛物线对称轴在y轴左侧，
∴b>0，
∵抛物线与y轴交点在x轴下方，
∴c<0，
∴直线y=ax+b经过第一，二，四象限，反比例函数y=-cx图象经过一，三象限，
故选：C．
由抛物线开口方向，对称轴位置及抛物线与y轴交点位置判断a，b，c的符号，从而可得直线与反比例函数图象的大致图象．
本题考查二次函数的性质，解题关键是掌握函数图象与系数的关系．

15.解：根据一次函数y=kx+b的图象位置，可判断k>0、b>0．
所以-k<0．
再根据一次函数和反比例函数的图像和性质，
故选：A．
本题形数结合，根据一次函数y=kx+b的图象位置，可判断k、b的符号；再由一次函数y=-kx+b，反比例函数y=bx中的系数符号，判断图象的位置．经历：图象位置-系数符号-图象位置．
本题考查一次函数和反比例函数的性质及数形结合思想的运用，故牢记函数的图像和性质是解题的关键．

16.解：由反比例函数y=k-2x的图象位于第二，四象限可知，k-2<0，
∴k<2，
∴k的值可以是1，
故答案为：1(答案不唯一)．
根据反比例函数的图象所处的位置确定k-2的符号，从而确定k的范围，可得答案．
考查了反比例函数的性质及图象，解题的关键是掌握反比例函数的性质，难度不大．

17.解：∵点C是OA的中点，
∴S△ACD=S△OCD，S△ACB=S△OCB，
∴S△ACD+S△ACB=S△OCD+S△OCB，
∴S△ABD=S△OBD，
∵点B在双曲线y=8x(x>0)上，BD⊥y轴，
∴S△OBD=12×8=4，
∴S△ABD=4，
故答案为：4．
根据三角形的中心把三角形分成相等的两部分，得到S△ACD=S△OCD，S△ACB=S△OCB，即可得到S△ABD=S△OBD，由反比例函数系数k的几何意义即可求得结论．
本题考查了反比例函数系数k的几何意义，三角形的面积，证得S△ABD=S△OBD是解题的关键．

18.解：令反比例函数为y=kx(k≠0)，
∵反比例函数的图象经过点(2,3)，
∴3=k2，
k=6，
∴反比例函数的解析式为y=6x．
故答案为：y=6x．
利用反比例函数的定义列函数的解析式，运用待定系数法求出函数的解析式即可．
考查反比例函数的解析式，关键要掌握利用待定系数法求解函数的解析式．

19.解：∵P=FS，F>0，
∴P随S的增大而减小，
∵A，B，C三个面的面积比是5：3：1，
∴P1，P2，P3的大小关系是：P3>P2>P1，
故答案为：P3>P2>P1．
根据反比例函数的性质解答即可．
本题考查了反比例函数的应用，正确把握反比例函数的性质是解题的关键．

20.解：∵点P(x,y)在双曲线y=kx的图象上，PA⊥x轴，
∴xy=k，OA=-x，PA=y．
∵S△AOP=2，
∴12×AO⋅PA=2．
∴-x⋅y=4．
∴xy=-4，
∴k=xy=-4．
∴该反比例函数的解析式为y=-4x．
故答案为：y=-4x．
利用待定系数法解答即可．
本题主要考查了反比例函数的几何意义，反比例函数图象上点的坐标的特征，待定系数法，利用点的坐标表示出相应线段的长度是解题的关键．

21.解：把R=220，I=1代入I=UR得：
1=U220，
解得U=220，
∴I=220R，
把R=55代入I=220R得：
I=22055=4，
故答案为：4．
由表格数据求出反比例函数的解析式，再将R=55Ω代入即可求出答案．
本题考查反比例函数的应用，解题的关键是根据已知求出反比例函数的解析式．

22.解：连接AA'，作B'E⊥x轴于点E，
由题意知OA=OA'，A'是OB中点，∠AOB=∠A'OB'，OB'=OB，
∴AA'=12OB=OA'，
∴△AOA'是等边三角形，
∴∠AOB=60°，
∴OB=2OA=2，∠B'OE=60°，
∴OB'=2，
∴OE=12OB'=1，
∴B'E=3OE=3，
∴B'(1,3)，
∵B'在反比例函数y=kx上，
∴k=1×3=3．
故答案为：3．
连接AA'，作B'E⊥x轴于点E，根据直角三角形斜边中线的性质和旋转的性质得出△AOA'是等边三角形，从而得出∠AOB=∠A'OB'=60°，即可得出∠B'OE=60°，解直角三角形求得B'的坐标，进一步求得k=3．
本题考查反比例函数图象上点的坐标特征，坐标与图形变化-性质，解答本题的关键是明确题意，利用数形结合的思想解答．

23.解：因为D为AC的中点，△AOD的面积为3，
所以△AOC的面积为6，
所以k=12=2m．
解得：m=6．
故答案为：6．
应用k的几何意义及中线的性质求解．
本题考查了反比例函数中k的几何意义，关键是利用△AOB的面积转化为三角形AOC的面积．

24.解：设点A(a,ka)，
∵AC⊥y轴，
∴AD=a，OD=ka，
∵ADAC=12，
∴AC=2a，
∴CD=3a，
∵BC⊥AC.AC⊥y轴，
∴BC/​/y轴，
∴点B(3a,k3a)，
∴BC=ka-k3a=2k3a，
∵S梯形OBCD=S△AOD+S四边形AOBC，
∴12(ka+2k3a)×3a=12k+6，
解得：k=3．
故答案为：3．
设点A(a,ka)，可得AD=a，OD=ka，从而得到CD=3a，再由BC⊥AC.可得点B(3a,k3a)，从而得到BC=2k3a，然后根据S梯形OBCD=S△AOD+S四边形AOBC，即可求解．
本题主要考查了反比例函数比例系数的几何意义，熟练掌握反比例函数比例系数的几何意义是解题的关键．

25.解：因为AE/​/BD，依据同底等高的原理，△BDF的面积等于△ABD的面积，
设B(a,3a)(a>0)，则0.5×3a⋅3a=9，
解得a=2，
所以3a2=6．
故k=6．
故答案为：6．
根据同底等高把面积进行转化，再根据k的几何意义，从而求出k的值．
本题考查了反比例函数系数k的几何意义，关键是根据同底等高把面积进行转化．

26.(1)先求a，再求解析式．
(2)数形结合，利用平行四边形的性质求D的坐标．
本题考查求反比例函数表达式及点的坐标，掌握待定系数法，充分利用平行四边形性质是求解本题的关键．

27.(1)利用待定系数法解答即可；
(2)利用直线的解析式求得点A坐标，利用坐标表示出线段CA，BC的长度，利用三角形的面积公式解答即可．
本题主要考查了待定系数法确定函数的解析式，一次函数图象的性质，一次函数图象上点的坐标的特征，反比例函数的性质，反比例函数图象上点的坐标的特征，利用点的坐标表示出相应线段的长度是解题的关键．

28.(1)过点B作BF⊥y轴，垂足为F，设点A为(0,m)，根据菱形的性质和勾股定理求出OA=BC=AB=5，然后求出点C的坐标，即可求出解析式；
(2)作DG⊥x轴，CH⊥x轴，垂足分别为G、H，先证明△ODG∽△OCH，求出OG=167，DG=127，然后得到点D的纵坐标，再求出点E的坐标即可．
本题考查了菱形的性质，反比例函数的图像和性质，相似三角形的判定和性质，勾股定理等知识，解题的关键是熟练理解题意，正确的作出辅助线，从而进行解题．

29.(1)利用反比例函数系数k的几何意义即可求得k的值，把B的坐标代入y=32x+b即可求得b的值，从而求得反比例和一次函数的解析式；
(2)利用两个函数的解析式求得D、E的坐标，进一步即可求得DE的长度．
本题是反比例函数与一次函数的交点问题，考查了待定系数法求一次函数的解析式，反比例函数系数k的几何意义，反比例函数、一次函数图象上点的坐标特征，求得函数的解析式是解题的关键．

30.(1)设密度ρ关于体积V的函数解析式为ρ=kV(k≠0)，利用反比例函数图象上点的坐标特征，即可求出k值，进而可得出密度ρ关于体积V的函数解析式；
(2)由k=9.9>0，利用反比例函数的性质可得出当V>0时ρ随V的增大而减小，结合V的取值范围，即可求出二氧化碳密度ρ的变化范围．
本题考查了反比例函数图象上点的坐标特征以及反比例函数的性质，解题的关键是：(1)利用反比例函数图象上点的坐标特征，求出k值；(2)利用反比例函数的性质及反比例函数图象上点的坐标特征，找出ρ的变化范围．

31.(1)把点A的坐标代入反比例函数解析式求出k2值，从而得到反比例函数解析式，再把点B的坐标代入反比例函数解析式求出m的值，然后利用待定系数法求函数解析式求出一次函数解析式；
(2)利用勾股定理求得OA，即可求得OD的长度，然后利用三角形面积公式求得即可．
本题是反比例函数图象与一次函数图象的交点问题，考查了待定系数法求函数的解析式，反比例函数图象上点的坐标特征，勾股定理的应用以及三角形面积，根据交点A的坐标求出反比例函数解析式以及点B的坐标是解题的关键．

32.(1)理解截距得概念，再利用待定系数法求解；
(2)数形结合，求两个点之间得距离，再利用三角函数得定义求解．
本题考查了待定系数法的应用，结合三角函数的定义求解是解题的关键．

33.(1)根据反比例函数图象上点的坐标特征求出k；
(2)求出点A的坐标，利用待定系数法求出直线AC的解析式，进而求出OB，根据三角形的面积公式计算，得到答案．
本题考查的是反比例函数图象上点的坐标特征、三角形的面积公式，灵活运用待定系数法求出直线AC的解析式是解题的关键．

34.(1)根据解析式求出B点的坐标，根据A点的坐标和B点的坐标得出三角形AOB的面积，根据面积比求出三角形COD的面积，设出C点的坐标，根据面积求出k的值，再用待定系数法求出p即可；
(2)根据C点的坐标得出E点的坐标，再根据面积相等列出方程求解即可．
本题主要考查反比例函数的图形和性质，一次函数的图象和性质，熟练掌握一次函数和反比例函数的图象和性质及待定系数法求函数解析式是解题的关键．

35.(1)把点B(2,6)代入反比例函数的关系式可求出k的值，利用相似三角形的性质可求出A的坐标，进而得出点C坐标；
(2)利用勾股定理求出OA、AC的长即可．
本题考查反比例函数图象上点的坐标特征，直角三角形的边角关系以及相似三角形的性质，掌握勾股定理，反比例函数图象上点的坐标特征以及相似三角形的性质是正确解答的前提．