2022年中考数学真题分类汇编：图形的旋转(含答案)

这是一份2022年中考数学真题分类汇编：图形的旋转(含答案)，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
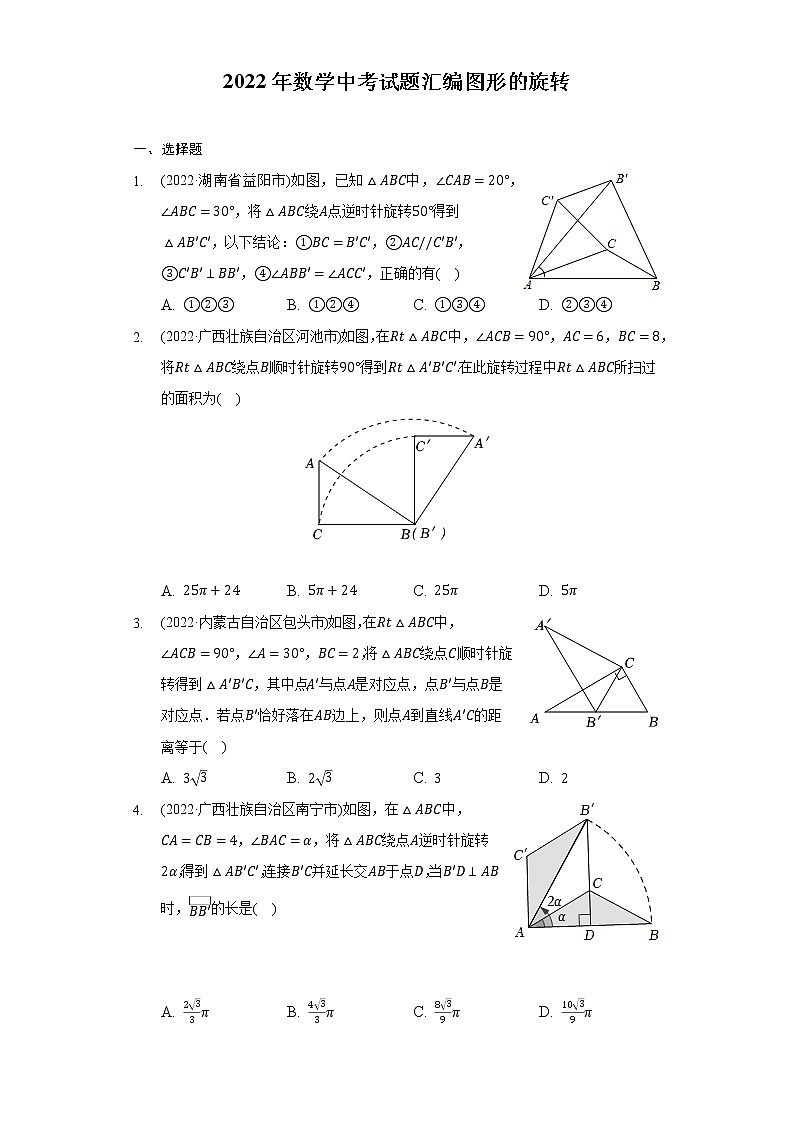
2022年数学中考试题汇编图形的旋转 一、选择题(2022·湖南省益阳市)如图，已知中，，，将绕点逆时针旋转得到，以下结论：，，，，正确的有(    )A.  B.  C.  D. (2022·广西壮族自治区河池市)如图，在中，，，，将绕点顺时针旋转得到在此旋转过程中所扫过的面积为(    )
A.  B.  C.  D. (2022·内蒙古自治区包头市)如图，在中，，，，将绕点顺时针旋转得到，其中点与点是对应点，点与点是对应点．若点恰好落在边上，则点到直线的距离等于(    )A.  B.  C.  D. (2022·广西壮族自治区南宁市)如图，在中，，，将绕点逆时针旋转，得到，连接并延长交于点，当时，的长是(    )  A.  B.  C.  D. (2022·内蒙古自治区赤峰市)如图，是的直径，将弦绕点顺时针旋转得到，此时点的对应点落在上，延长，交于点，若，则图中阴影部分的面积为(    )A. B. C. D. (2022·天津市)如图，在中，，若是边上任意一点，将绕点逆时针旋转得到，点的对应点为点，连接，则下列结论一定正确的是(    )A. B. C. D. (2022·贵州省遵义市)在平面直角坐标系中，点与点关于原点成中心对称，则的值为(    )A.  B.  C.  D. (2022·湖南省娄底市)如图，等边内切的图形来自我国古代的太极图，等边三角形内切圆中的黑色部分和白色部分关于等边的内心成中心对称，则圆中的黑色部分的面积与的面积之比是(    )  A.  B.  C.  D. (2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是(    )A.  B. C.  D. (2022·湖南省娄底市)下列与年冬奥会相关的图案中，是中心对称图形的是(    )A.  B. C.  D. (2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是(    )A.  B. C.  D. (2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是(    )A.  B. C.  D. (2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是(    )A.  B. C.  D. (2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是(    )A.  B. C.  D. (2022·湖南省)下列图形中，既是轴对称图形又是中心对称图形的是(    )A.  B. C.  D. (2022·上海市)有一个正边形旋转后与自身重合，则为(    )A.  B.  C.  D.  二、填空题(2022·青海省西宁市)如图，在中，，，，将绕点逆时针方向旋转得到，交于点，则______．
(2022·湖北省随州市)如图，在矩形中，，，，分别为，的中点，连接如图，将绕点逆时针旋转角，使，连接并延长交于点则的度数为          ，的长为          ．
(2022·吉林省)第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素．如图，这个图案绕着它的中心旋转角后能够与它本身重合，则角可以为______度．写出一个即可 (2022·辽宁省盘锦市)如图，在中，，，点为的中点，将绕点逆时针旋转得到，当点的对应点落在边上时，点在的延长线上，连接，若，则的面积是______．
(2022·湖南省永州市)如图，图中网格由边长为的小正方形组成，点为网格线的交点．若线段绕原点顺时针旋转后，端点的坐标变为______．    三、解答题(2022·广西壮族自治区河池市)如图、在平面直角坐标系中，的三个顶点的坐标分别为，，．画出与关于轴对称的；以原点为位似中心，在第三象限内画一个，使它与的相似比为：，并写出点的坐标．
(2022·吉林省)图，图均是的正方形网格，每个小正方形的顶点称为格点．其中点，，均在格点上，请在给定的网格中按要求画四边形．在图中，找一格点，使以点，，，为顶点的四边形是轴对称图形；在图中，找一格点，使以点，，，为顶点的四边形是中心对称图形． 
(2022·江苏省常州市)如图，点在射线上，如果绕点按逆时针方向旋转到，那么点的位置可以用表示．  按上述表示方法，若，，则点的位置可以表示为______；在的条件下，已知点的位置用表示，连接、求证：．(2022·湖北省武汉市)如图是由小正方形组成的网格，每个小正方形的顶点叫做格点．的三个顶点都是格点．仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示．在图中，，分别是边，与网格线的交点．先将点绕点旋转得到点，画出点，再在上画点，使；在图中，是边上一点，先将绕点逆时针旋转，得到线段，画出线段，再画点，使，两点关于直线对称． 
(2022·四川省广安市)数学活动课上，张老师组织同学们设计多姿多彩的几何图形，如图都是由边长为的小等边三角形构成的网格，每个网格图中有个小等边三角形已涂上阴影，请同学们在余下的空白小等边三角形中选取一个涂上阴影，使得个阴影小等边三角形组成一个轴对称图形或中心对称图形，请画出种不同的设计图形．规定：凡通过旋转能重合的图形视为同一种图形， 

 1.【答案】 【解析】解：绕点逆时针旋转得到，故正确；绕点逆时针旋转，．，．，．故正确；在中，，，．．与不垂直．故不正确；在中，，，．故正确．这三个结论正确．故选：．2.【答案】 【解析】解：，，，，所扫过的面积，故选：．3.【答案】 【解析】解：连接，如图， ，，，，，将绕点顺时针旋转得到，，，，，，为等边三角形，，，为等边三角形，过点作于点，，，点到直线的距离为，故选：．4.【答案】 【解析】解：根据题意可得，，，，，，，，，，的长度．故选：．5.【答案】 【解析】解：连接，，， 由旋转知，，，，，，，即为等腰直角三角形，，，，故选：．6.【答案】 【解析】解：、，，由旋转的性质可知，，，故本选项结论错误，不符合题意；B、当为等边三角形时，，除此之外，与不平行，故本选项结论错误，不符合题意；C、由旋转的性质可知，，，，，，，本选项结论正确，符合题意；D、只有当点为的中点时，，才有，故本选项结论错误，不符合题意；故选：．7.【答案】 【解析】解：点与点关于原点成中心对称，，，，故选：．8.【答案】 【解析】解：作于点，作于点，和交于点，如图所示，设，则，，，，圆中的黑色部分的面积与的面积之比是：，故选：．9.【答案】 【解析】解：是轴对称图形，不是中心对称图形，故本选项错误；B.不是轴对称图形，是中心对称图形，故本选项错误；C.既是轴对称图形，又是中心对称图形，故本选项正确；D.是轴对称图形，不是中心对称图形，故本选项错误．故选C．  10.【答案】 【解析】解：不是中心对称图形，故此选项不合题意；B.不是中心对称图形，故此选项不合题意；C.不是中心对称图形，故此选项不合题意；D.是中心对称图形，故此选项符合题意；故选：．11.【答案】 【解析】解：是中心对称图形，不是轴对称图形，故此选项不合题意；B.不是中心对称图形，也不是轴对称图形，故此选项不合题意；C.不是中心对称图形，是轴对称图形，故此选项不合题意；D.既是中心对称图形，也是轴对称图形，故此选项符合题意；故选：．12.【答案】 【解析】解：不是中心对称图形，是轴对称图形，故此选项不合题意；B.是中心对称图形，不是轴对称图形，故此选项不合题意；C.不是中心对称图形，是轴对称图形，故此选项不合题意；D.既是中心对称图形，也是轴对称图形，故此选项符合题意；故选：．13.【答案】 【解析】解：是轴对称图形，不是中心对称图形，故此选项不合题意；B.是轴对称图形，不是中心对称图形，故此选项不合题意；C.既是轴对称图形又是中心对称图形，故此选项符合题意；D.是轴对称图形，不是中心对称图形，故此选项不合题意；故选：．14.【答案】 【解析】解：既不是中心对称图形，也不是轴对称图形，故此选项不合题意；B.既不是中心对称图形，也不是轴对称图形，故此选项不合题意；C.既是中心对称图形，也是轴对称图形，故此选项符合题意；D.不是中心对称图形，是轴对称图形，故此选项不合题意；故选：．15.【答案】 【解析】解：不是中心对称图形，是轴对称图形，故此选项不合题意；B.是中心对称图形，不是轴对称图形，故此选项不合题意；C.既是中心对称图形，也是轴对称图形，故此选项符合题意；D.不是中心对称图形，是轴对称图形，故此选项不合题意；故选：．16.【答案】 【解析】解：正边形旋转后不能与自身重合，不合题意；B.正边形旋转后不能与自身重合，不合题意；C.正边形旋转后能与自身重合，符合题意；D.正边形旋转后不能与自身重合，不合题意；故选：．17.【答案】 【解析】解：在中，，，，，，，将绕点逆时针方向旋转得到，≌，，，，．先在含锐角的直角三角形中计算出两条直角边，再根据旋转性质得到对应边相等、对应角相等得到，，即可解答．18.【解析】解：如图，设交于点，交于点，过点作于点．，，，，∽，，，，，，，，，，，，，，，，，，，，，，，．故答案为：，．19.【答案】答案不唯一． 【解析】解：，则这个图案绕着它的中心旋转后能够与它本身重合，故答案为：答案不唯一．20.【答案】 【解析】解：如下图所示，设与交于点，连接和，  点为的中点，，，，，是的角平分线，是，，，，，是等边三角形，，，，，，，，，，，，，．先证明是等边三角形，再证明，再利用直角三角形角对应的边是斜边的一半分别求出和，再利用勾股定理求出，从而求得的面积．21.【答案】 【解析】解：线段绕原点顺时针旋转如图所示，则， 则旋转后点坐标变为：，故答案为：．22.【答案】解：如图，为所作；如图，为所作，点的坐标为； 【解析】根据关于轴对称的点的坐标得到、、的坐标，然后描点即可；把、、的坐标都乘以得到、、的坐标，然后描点即可．本题考查了位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为，那么位似图形对应点的坐标的比等于或也考查了轴对称变换． 23.【答案】解：作点关于直线的对称点，连接，四边形为筝形，符合题意． 将点向右平移个单位，再向上平移个单位可得点，连接，且，四边形为矩形，符合题意． 24.【答案】解：由题意，得，，，，故答案为：；证明：如图：，，，，，，，≌，． 25.【答案】解：如图中，点，点即为所求；如图中，线段，点即为所求． 26.【答案】解：图形如图所示： 【解析】利用轴对称图形，中心对称图形的性质，画出图形即可．本题考查利用作图设计图案，等边三角形的判定和性质，轴对称图形，中心对称图形等知识，解题的关键是理解题意，灵活运用所学知识解决问题．