2022年山东省泰安市岱岳区中考数学押题试卷含解析

这是一份2022年山东省泰安市岱岳区中考数学押题试卷含解析，共24页。试卷主要包含了答题时请按要求用笔，下列各数是不等式组的解是等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．据财政部网站消息，2018年中央财政困难群众救济补助预算指标约为929亿元，数据929亿元科学记数法表示为（　　）
A．9.29×109 B．9.29×1010 C．92.9×1010 D．9.29×1011
2．某市2017年实现生产总值达280亿的目标，用科学记数法表示“280亿”为（　　）
A．28×109 B．2.8×108 C．2.8×109 D．2.8×1010
3．汽车刹车后行驶的距离s（单位：m）关于行驶的时间t（单位：s）的函数解析式是s=20t﹣5t2，汽车刹车后停下来前进的距离是（　　）
A．10m B．20m C．30m D．40m
4．如图，在中，，分别以点和点为圆心，以大于的长为半径作弧，两弧相交于点和点，作直线交于点，交于点，连接.若，则的度数是（ ）

A． B． C． D．
5．如图，以O为圆心的圆与直线交于A、B两点，若△OAB恰为等边三角形，则弧AB的长度为（ ）

A． B．π C．π D．π
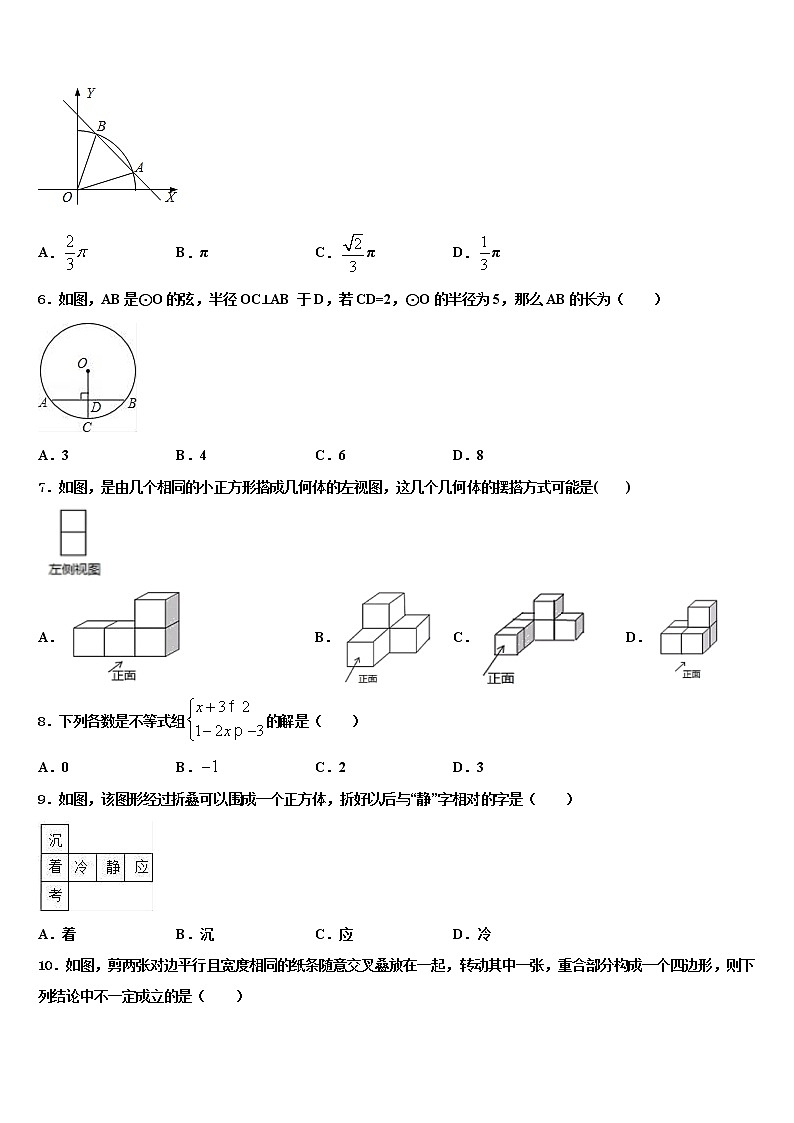
6．如图，AB是⊙O的弦，半径OC⊥AB 于D，若CD=2，⊙O的半径为5，那么AB的长为（　　）

A．3 B．4 C．6 D．8
7．如图，是由几个相同的小正方形搭成几何体的左视图，这几个几何体的摆搭方式可能是( )

A． B． C． D．
8．下列各数是不等式组的解是（　　）
A．0 B． C．2 D．3
9．如图，该图形经过折叠可以围成一个正方体，折好以后与“静”字相对的字是（ ）

A．着 B．沉 C．应 D．冷
10．如图，剪两张对边平行且宽度相同的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（　　）

A．∠ABC＝∠ADC，∠BAD＝∠BCD B．AB＝BC
C．AB＝CD，AD＝BC D．∠DAB+∠BCD＝180°
11．如图，BC⊥AE于点C，CD∥AB，∠B＝55°，则∠1等于（　　）

A．35° B．45° C．55° D．25°
12．共享单车为市民出行带来了方便，某单车公司第一个月投放1000辆单车，计划第三个月投放单车数量比第一个月多440辆．设该公司第二、三两个月投放单车数量的月平均增长率为x，则所列方程正确的为（　　）
A．1000（1+x）2＝1000+440 B．1000（1+x）2＝440
C．440（1+x）2＝1000 D．1000（1+2x）＝1000+440
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．如图，在△ABC中，DE∥BC，BF平分∠ABC，交DE的延长线于点F，若AD=1，BD=2，BC=4，则EF=________．

14．关于x的一元二次方程x2﹣2x+m﹣1＝0有两个实数根，则m的取值范围是_____．
15．从﹣2，﹣1，2，0这四个数中任取两个不同的数作为点的坐标，该点不在第三象限的概率是_____．
16．不等式组的解集是_____．
17．某校组织“优质课大赛”活动，经过评比有两名男教师和两名女教师获得一等奖，学校将从这四名教师中随机挑选两位教师参加市教育局组织的决赛，挑选的两位教师恰好是一男一女的概率为____．
18．已知点A(x1，y1)，B(x2，y2)在直线y＝kx＋b上，且直线经过第一、三、四象限，当x1＜x2时，y1与y2的大小关系为______________．
三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）如图，已知反比例函数和一次函数的图象相交于第一象限内的点A，且点A的横坐标为1.过点A作AB⊥x轴于点B，△AOB的面积为1.
求反比例函数和一次函数的解析式.若一次函数的图象与x轴相交于点C，求∠ACO的度数.结合图象直接写出：当＞＞0时，x的取值范围.
20．（6分）由于雾霾天气趋于严重，我市某电器商城根据民众健康需求，代理销售某种家用空气净化器，其进价是200元/台.经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务．完成下列表格，并直接写出月销售量y（台）与售价x（元/台）之间的函数关系式及售价x的取值范围；
售价（元/台）
月销售量（台）
400
200

250
x

（2）当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？
21．（6分）已知：如图，四边形ABCD的对角线AC和BD相交于点E，AD=DC，DC2=DE•DB，求证：
（1）△BCE∽△ADE；
（2）AB•BC=BD•BE．

22．（8分）如图，反比例y=的图象与一次函数y=kx﹣3的图象在第一象限内交于A（4，a）．
（1）求一次函数的解析式；
（2）若直线x=n（0＜n＜4）与反比例函数和一次函数的图象分别交于点B，C，连接AB，若△ABC是等腰直角三角形，求n的值．

23．（8分）如图1，定义：在直角三角形ABC中，锐角α的邻边与对边的比叫做角α的余切，记作ctanα，即ctanα＝＝，根据上述角的余切定义，解下列问题：
（1）如图1，若BC＝3，AB＝5，则ctanB＝_____；
（2）ctan60°＝_____；
（3）如图2，已知：△ABC中，∠B是锐角，ctan C＝2，AB＝10，BC＝20，试求∠B的余弦cosB的值．

24．（10分）如图，点B、E、C、F在同一条直线上，AB＝DE，AC＝DF，BE＝CF，求证：AB∥DE．

25．（10分）如图，已知一次函数的图象与反比例函数的图象交于点，与轴、轴交于两点，过作垂直于轴于点.已知.
（1）求一次函数和反比例函数的表达式；
（2）观察图象:当时，比较.

26．（12分）如图1，在Rt△ABC中，∠C=90°，AC=BC=2，点D、E分别在边AC、AB上，AD=DE=AB，连接DE．将△ADE绕点A逆时针方向旋转，记旋转角为θ．
（1）问题发现
①当θ=0°时，= ；
②当θ=180°时，= ．
（2）拓展探究
试判断：当0°≤θ＜360°时，的大小有无变化？请仅就图2的情形给出证明；
（3）问题解决
①在旋转过程中，BE的最大值为 ；
②当△ADE旋转至B、D、E三点共线时，线段CD的长为 ．

27．（12分）如图是小强洗漱时的侧面示意图，洗漱台（矩形ABCD）靠墙摆放，高AD＝80cm，宽AB＝48cm，小强身高166cm，下半身FG＝100cm，洗漱时下半身与地面成80°（∠FGK＝80°），身体前倾成125°（∠EFG＝125°），脚与洗漱台距离GC＝15cm（点D，C，G，K在同一直线上）．（cos80°≈0.17，sin80°≈0.98，≈1.414）

（1）此时小强头部E点与地面DK相距多少？
（2）小强希望他的头部E恰好在洗漱盆AB的中点O的正上方，他应向前或后退多少？



参考答案

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、B
【解析】
科学记数法的表示形式为a×1n的形式，其中1≤|a|＜1，n为整数．确定n的值是易错点，由于929亿有11位，所以可以确定n=11-1=1．
【详解】
解：929亿=92900000000=9.29×11．
故选B．
【点睛】
此题考查科学记数法表示较大的数的方法，准确确定a与n值是关键．
2、D
【解析】
根据科学计数法的定义来表示数字，选出正确答案.
【详解】
解：把一个数表示成a（1≤a<10，n为整数）与10的幂相乘的形式，这种记数法叫做科学记数法，280亿用科学计数法表示为2.8×1010，所以答案选D.
【点睛】
本题考查学生对科学计数法的概念的掌握和将数字用科学计数法表示的能力.
3、B
【解析】
利用配方法求二次函数最值的方法解答即可．
【详解】
∵s=20t-5t2=-5（t-2）2+20，
∴汽车刹车后到停下来前进了20m．
故选B．
【点睛】
此题主要考查了利用配方法求最值的问题，根据已知得出顶点式是解题关键．
4、B
【解析】
根据题意可知DE是AC的垂直平分线，CD=DA．即可得到∠DCE=∠A，而∠A和∠B互余可求出∠A，由三角形外角性质即可求出∠CDA的度数.
【详解】
解：∵DE是AC的垂直平分线，
∴DA=DC，
∴∠DCE=∠A，
∵∠ACB=90°，∠B=34°，
∴∠A=56°，
∴∠CDA=∠DCE+∠A=112°，
故选B．
【点睛】
本题考查作图-基本作图、线段的垂直平分线的性质、等腰三角形的性质，三角形有关角的性质等知识，解题的关键是熟练运用这些知识解决问题，属于中考常考题型．
5、C
【解析】
过点作，
∵，

∴，，
∴为等腰直角三角形，，
，
∵为等边三角形，
∴，
∴．
∴．故选C.
6、D
【解析】
连接OA，构建直角三角形AOD；利用垂径定理求得AB=2AD；然后在直角三角形AOD中由勾股定理求得AD的长度，从而求得AB=2AD=1．
【详解】
连接OA．

∵⊙O的半径为5，CD=2，
∵OD=5-2=3，即OD=3；
又∵AB是⊙O的弦，OC⊥AB，
∴AD=AB；
在直角三角形ODC中，根据勾股定理，得
AD==4，
∴AB=1．
故选D．
【点睛】
本题考查了垂径定理、勾股定理．解答该题的关键是通过作辅助线OA构建直角三角形，在直角三角形中利用勾股定理求相关线段的长度．
7、A
【解析】
根据左视图的概念得出各选项几何体的左视图即可判断．
【详解】
解：A选项几何体的左视图为
；
B选项几何体的左视图为
；
C选项几何体的左视图为
；
D选项几何体的左视图为
；
故选：A．
【点睛】
本题考查由三视图判断几何体，解题的关键是熟练掌握左视图的概念．
8、D
【解析】
求出不等式组的解集，判断即可．
【详解】
，
由①得：x＞-1，
由②得：x＞2，
则不等式组的解集为x＞2，即3是不等式组的解，
故选D．
【点睛】
此题考查了解一元一次不等式组，熟练掌握运算法则是解本题的关键．
9、A
【解析】
正方体的平面展开图中，相对面的特点是中间必须间隔一个正方形，据此作答
【详解】
这是一个正方体的平面展开图，共有六个面，其中面“沉”与面“考”相对，面“着”与面“静”相对，“冷”与面“应”相对．
故选：A
【点睛】
本题主要考查了利用正方体及其表面展开图的特点解题，明确正方体的展开图的特征是解决此题的关键
10、D
【解析】
首先可判断重叠部分为平行四边形，且两条纸条宽度相同；再由平行四边形的等积转换可得邻边相等，则四边形为菱形．所以根据菱形的性质进行判断．
【详解】
解:

四边形是用两张等宽的纸条交叉重叠地放在一起而组成的图形，
，，
四边形是平行四边形（对边相互平行的四边形是平行四边形）；
过点分别作，边上的高为，．则
（两纸条相同，纸条宽度相同）；
平行四边形中，，即，
，即．故正确；
平行四边形为菱形（邻边相等的平行四边形是菱形）．
，（菱形的对角相等），故正确；
，（平行四边形的对边相等），故正确；
如果四边形是矩形时，该等式成立．故不一定正确．
故选：．
【点睛】
本题考查了菱形的判定与性质．注意：“邻边相等的平行四边形是菱形”，而非“邻边相等的四边形是菱形”．
11、A
【解析】
根据垂直的定义得到∠∠BCE=90°，根据平行线的性质求出∠BCD=55°，计算即可．
【详解】
解：∵BC⊥AE，
∴∠BCE=90°，
∵CD∥AB，∠B=55°，
∴∠BCD=∠B=55°，
∴∠1=90°-55°=35°，
故选：A．
【点睛】
本题考查的是平行线的性质和垂直的定义，两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
12、A
【解析】
根据题意可以列出相应的一元二次方程，从而可以解答本题．
【详解】
解：由题意可得，
1000（1+x）2＝1000+440，
故选：A．
【点睛】
此题主要考查一元二次方程的应用，解题的关键是根据题意找到等量关系进行列方程.

二、填空题：（本大题共6个小题，每小题4分，共24分．）
13、
【解析】
由DE∥BC可得出△ADE∽△ABC，根据相似三角形的性质和平行线的性质解答即可．
【详解】
∵DE∥BC，
∴∠F=∠FBC，
∵BF平分∠ABC，
∴∠DBF=∠FBC，
∴∠F=∠DBF，
∴DB=DF，
∵DE∥BC，
∴△ADE∽△ABC，
∴ ，即 ，
解得：DE= ，
∵DF=DB=2，
∴EF=DF-DE=2- = ，
故答案为.
【点睛】
此题考查相似三角形的判定和性质，关键是由DE∥BC可得出△ADE∽△ABC．
14、m≤1
【解析】
根据一元二次方程有实数根，得出△≥0，建立关于m的不等式，求出m的取值范围即可．
【详解】
解：由题意知，△＝4﹣4（m﹣1）≥0，
∴m≤1，
故答案为：m≤1．
【点睛】
此题考查了根的判别式，掌握一元二次方程根的情况与判别式△的关系：△＞0，方程有两个不相等的实数根；△＝0，方程有两个相等的实数根；△＜0，方程没有实数根是本题的关键．
15、
【解析】
列举出所有情况，看在第四象限的情况数占总情况数的多少即可．
【详解】
如图：

共有12种情况，在第三象限的情况数有2种，
故不再第三象限的共10种，
不在第三象限的概率为，
故答案为．
【点睛】
本题考查了树状图法的知识，解题的关键是列出树状图求出概率．
16、2＜x≤1
【解析】
本题可根据不等式组分别求出每一个不等式的解集，然后即可确定不等式组的解集．
【详解】
由①得x＞2，
由②得x≤1，
∴不等式组的解集为2＜x≤1．
故答案为：2＜x≤1．
【点睛】
此题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解，求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．
17、
【解析】
根据列表法求出所有可能及可得出挑选的两位教师恰好是一男一女的结果数而利用概率公式计算可得．
【详解】
解：所有可能的结果如下表：

男1
男2
女1
女2
男1

（男1，男2）
（男1，女1）
（男1，女2）
男2
（男2，男1）

（男2，女1）
（男2，女2）
女1
（女1，男1）
（女1，男2）

（女1，女2）
女2
（女2，男1）
（女2，男2）
（女2，女1）

由表可知总共有12种结果，每种结果出现的可能性相同．挑选的两位教师恰好是一男一女的结果有8种，
所以其概率为挑选的两位教师恰好是一男一女的概率为=，
故答案为．
【点睛】
本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．
18、y1 【解析】
直接利用一次函数的性质分析得出答案．
【详解】
解：∵直线经过第一、三、四象限，
∴y随x的增大而增大，
∵x1＜x1，
∴y1与y1的大小关系为：y1＜y1．
故答案为：y1 【点睛】
此题主要考查了一次函数图象上点的坐标特征，正确掌握一次函数增减性是解题关键．

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、（1）y=；y=x+1；（2）∠ACO=45°；（3）0 【解析】
（1）根据△AOB的面积可求AB，得A点坐标．从而易求两个函数的解析式；
（2）求出C点坐标，在△ABC中运用三角函数可求∠ACO的度数；
（3）观察第一象限内的图形，反比例函数的图象在一次函数的图象的上面部分对应的x的值即为取值范围．
【详解】
(1)∵△AOB的面积为1，并且点A在第一象限，
∴k=2,∴y=；
∵点A的横坐标为1，
∴A(1,2).
把A(1,2)代入y=ax+1得，a=1.
∴y=x+1.
(2)令y=0，0=x+1，
∴x=−1,
∴C(−1,0).
∴OC=1，BC=OB+OC=2.
∴AB=CB,
∴∠ACO=45°.
(3)由图象可知,在第一象限,当y>y>0时,0 在第三象限,当y>y>0时,−1 【点睛】
此题考查反比例函数与一次函数的交点问题，解题关键在于结合函数图象进行解答.
20、 (1)390,1-5x,y=-5x+1(300≤x≤2);(2)售价定位320元时，利润最大，为3元.
【解析】
（1）根据题中条件可得390，1-5x，若销售价每降低10元，月销售量就可多售出50千克，即可列出函数关系式；根据供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售即可求出x的取值．
（2）用x表示y，然后再用x来表示出w，根据函数关系式，即可求出最大w.
【详解】
(1)依题意得：
y＝200＋50×．
化简得：y＝－5x＋1．
(2)依题意有：
∵，
解得300≤x≤2．
(3)由(1)得：w＝(－5x＋1)(x－200)
＝－5x2＋3200x－440000＝－5(x－320)2＋3．
∵x＝320在300≤x≤2内，∴当x＝320时，w最大＝3．
即售价定为320元/台时，可获得最大利润为3元．
【点睛】
本题考查了利润率问题的数量关系的运用，一次函数的解析式的运用，二次函数的解析式的运用，一元二次方程的解法的运用，解答时求出二次函数的解析式时关键．
21、（1）见解析；（2）见解析.
【解析】
（1）由∠DAC=∠DCA，对顶角∠AED=∠BEC，可证△BCE∽△ADE．
（2）根据相似三角形判定得出△ADE∽△BDA，进而得出△BCE∽△BDA，利用相似三角形的性质解答即可．
【详解】
证明：（1）∵AD=DC，
∴∠DAC=∠DCA，
∵DC2=DE•DB，
∴=，∵∠CDE=∠BDC，
∴△CDE∽△BDC，
∴∠DCE=∠DBC，
∴∠DAE=∠EBC，
∵∠AED=∠BEC，
∴△BCE∽△ADE，
（2）∵DC2=DE•DB，AD=DC
∴AD2=DE•DB，
同法可得△ADE∽△BDA，
∴∠DAE=∠ABD=∠EBC，
∵△BCE∽△ADE，
∴∠ADE=∠BCE，
∴△BCE∽△BDA，
∴=，
∴AB•BC=BD•BE．

【点睛】
本题考查了相似三角形的判定与性质．关键是要懂得找相似三角形，利用相似三角形的性质求解．
22、（1）y=x﹣3（2）1
【解析】
（1）由已知先求出a，得出点A的坐标，再把A的坐标代入一次函数y=kx-3求出k的值即可求出一次函数的解析式；
（2）易求点B、C的坐标分别为（n，），（n，n-3）．设直线y=x-3与x轴、y轴分别交于点D、E，易得OD=OE=3，那么∠OED=45°．根据平行线的性质得到∠BCA=∠OED=45°，所以当△ABC是等腰直角三角形时只有AB=AC一种情况．过点A作AF⊥BC于F，根据等腰三角形三线合一的性质得出BF=FC，依此得出方程-1=1-（n-3），解方程即可．
【详解】
解：（1）∵反比例y=的图象过点A（4，a），
∴a==1，
∴A（4，1），
把A（4，1）代入一次函数y=kx﹣3，得4k﹣3=1，
∴k=1，
∴一次函数的解析式为y=x﹣3；
（2）由题意可知，点B、C的坐标分别为（n，），（n，n﹣3）．
设直线y=x﹣3与x轴、y轴分别交于点D、E，如图，

当x=0时，y=﹣3；当y=0时，x=3，
∴OD=OE，
∴∠OED=45°．
∵直线x=n平行于y轴，
∴∠BCA=∠OED=45°，
∵△ABC是等腰直角三角形，且0＜n＜4，
∴只有AB=AC一种情况，
过点A作AF⊥BC于F，则BF=FC，F（n，1），
∴﹣1=1﹣（n﹣3），
解得n1=1，n2=4，
∵0＜n＜4，
∴n2=4舍去，
∴n的值是1．
【点睛】
本题考查了反比例函数与一次函数的交点问题，待定系数法求一次函数的解析式，等腰直角三角形的性质，难度适中．
23、（1）；（2）；（3）．
【解析】
试题分析：（1）先利用勾股定理计算出AC=4，然后根据余切的定义求解；
（2）根据余切的定义得到ctan60°=，然后把tan60°=代入计算即可；
（3）作AH⊥BC于H，如图2，先在Rt△ACH中利用余切的定义得到ctanC==2，则可设AH=x，CH=2x，BH=BC﹣CH=20﹣2x，接着再在Rt△ABH中利用勾股定理得到（20﹣2x）2+x2=102，解得x1=6，x2=10（舍去），所以BH=8，然后根据余弦的定义求解．
解：（1）∵BC=3，AB=5，
∴AC==4，
∴ctanB==；
（2）ctan60°===；
（3）作AH⊥BC于H，如图2，
在Rt△ACH中，ctanC==2，
设AH=x，则CH=2x，
∴BH=BC﹣CH=20﹣2x，
在Rt△ABH中，∵BH2+AH2=AB2，
∴（20﹣2x）2+x2=102，解得x1=6，x2=10（舍去），
∴BH=20﹣2×6=8，
∴cosB===．

考点：解直角三角形．
24、详见解析.
【解析】
试题分析：利用SSS证明△ABC≌△DEF，根据全等三角形的性质可得∠B=∠DEF，再由平行线的判定即可得AB∥DE．
试题解析：证明：由BE＝CF可得BC＝EF，
又AB＝DE，AC＝DF，
故△ABC≌△DEF（SSS），
则∠B=∠DEF，
∴AB∥DE．
考点：全等三角形的判定与性质.
25、（1）;（2）
【解析】
（1）由一次函数的解析式可得出D点坐标，从而得出OD长度，再由△ODC与△BAC相似及AB与BC的长度得出C、B、A的坐标，进而算出一次函数与反比例函数的解析式；
（2）以A点为分界点，直接观察函数图象的高低即可知道答案．
【详解】
解：（1）对于一次函数y=kx-2，令x=0，则y=-2，即D（0，-2），
∴OD=2，
∵AB⊥x轴于B，
∴ ，
∵AB=1，BC=2，
∴OC=4，OB=6，
∴C（4，0），A（6，1）
将C点坐标代入y=kx-2得4k-2=0，
∴k=，
∴一次函数解析式为y=x-2；
将A点坐标代入反比例函数解析式得m=6，
∴反比例函数解析式为y=；
（2）由函数图象可知：
当0＜x＜6时，y1＜y2；
当x=6时，y1=y2；
当x＞6时，y1＞y2；
【点睛】
本题考查了反比例函数与一次函数的交点问题．熟悉函数图象上点的坐标特征和待定系数法解函数解析式的方法是解答本题的关键，同时注意对数形结合思想的认识和掌握．
26、（1）①；（2）无变化，证明见解析；（3）①2+2 +1或﹣1.
【解析】
（1）①先判断出DE∥CB，进而得出比例式，代值即可得出结论；②先得出DE∥BC，即可得出，，再用比例的性质即可得出结论；（2）先∠CAD=∠BAE，进而判断出△ADC∽△AEB即可得出结论；（3）分点D在BE的延长线上和点D在BE上，先利用勾股定理求出BD，再借助（2）结论即可得出CD．
【详解】
解：（1）①当θ=0°时，
在Rt△ABC中，AC=BC=2，
∴∠A=∠B=45°，AB=2，
∵AD=DE=AB=，
∴∠AED=∠A=45°，
∴∠ADE=90°，
∴DE∥CB，
∴，
∴，
∴，
故答案为，
②当θ=180°时，如图1，

∵DE∥BC，
∴，
∴，
即：，
∴，
故答案为；
（2）当0°≤θ＜360°时，的大小没有变化，
理由：∵∠CAB=∠DAE，
∴∠CAD=∠BAE，
∵，
∴△ADC∽△AEB，
∴；
（3）①当点E在BA的延长线时，BE最大，
在Rt△ADE中，AE=AD=2，
∴BE最大=AB+AE=2+2；
②如图2，

当点E在BD上时，
∵∠ADE=90°，
∴∠ADB=90°，
在Rt△ADB中，AB=2，AD=，根据勾股定理得，BD==，
∴BE=BD+DE=+，
由（2）知，，
∴CD=+1，
如图3，

当点D在BE的延长线上时，
在Rt△ADB中，AD=，AB=2，根据勾股定理得，BD==，
∴BE=BD﹣DE=﹣，
由（2）知，，
∴CD=﹣1．
故答案为 +1或﹣1．
【点睛】
此题是相似形综合题，主要考查了等腰直角三角形的性质和判定，勾股定理，相似三角形的判定和性质，比例的基本性质及分类讨论的数学思想，解（1）的关键是得出DE∥BC，解（2）的关键是判断出△ADC∽△AEB，解（3）关键是作出图形求出BD，是一道中等难度的题目．
27、 (1) 小强的头部点E与地面DK的距离约为144.5 cm.(2) 他应向前9.5 cm.
【解析】
试题分析：（1）过点F作FN⊥DK于N，过点E作EM⊥FN于M．求出MF、FN的值即可解决问题；
（2）求出OH、PH的值即可判断；
试题解析：解：（1）过点F作FN⊥DK于N，过点E作EM⊥FN于M．
∵EF+FG=166，FG=100，∴EF=66，∵∠FGK=80°，∴FN=100sin80°≈98，∵∠EFG=125°，∴∠EFM=180°﹣125°﹣10°=45°，∴FM=66cos45°=≈46.53，∴MN=FN+FM≈144.5，∴此时小强头部E点与地面DK相距约为144.5cm．
（2）过点E作EP⊥AB于点P，延长OB交MN于H．∵AB=48，O为AB中点，∴AO=BO=24，∵EM=66sin45°≈46.53，∴PH≈46.53，∵GN=100cos80°≈17，CG=15，∴OH=24+15+17=56，OP=OH﹣PH=56﹣46.53=9.47≈9.5，∴他应向前9.5cm．