2022年浙江省嘉兴市秀洲区中考数学最后冲刺模拟试卷含解析

这是一份2022年浙江省嘉兴市秀洲区中考数学最后冲刺模拟试卷含解析，共20页。试卷主要包含了近似数精确到，下列运算正确的是，如图所示的几何体的俯视图是等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1．如图，在平面直角坐标系中，矩形OABC的两边OA，OC分别在x轴和y轴上，并且OA=5，OC=1．若把矩形OABC绕着点O逆时针旋转，使点A恰好落在BC边上的A1处，则点C的对应点C1的坐标为（　　）

A．（﹣） B．（﹣） C．（﹣） D．（﹣）
2．小红上学要经过三个十字路口，每个路口遇到红、绿灯的机会都相同，小红希望小学时经过每个路口都是绿灯，但实际这样的机会是（ ）
A． B． C． D．
3．﹣3的相反数是（ ）
A． B． C． D．
4．三角形两边的长是3和4，第三边的长是方程x2－12x＋35＝0的根，则该三角形的周长为（ ）
A．14 B．12 C．12或14 D．以上都不对
5．在围棋盒中有x颗白色棋子和y颗黑色棋子，从盒中随机取出一颗棋子，取得白色棋子的概率是，如再往盒中放进3颗黑色棋子，取得白色棋子的概率变为，则原来盒里有白色棋子（　　）
A．1颗 B．2颗 C．3颗 D．4颗
6．近似数精确到（ ）
A．十分位 B．个位 C．十位 D．百位
7．不透明袋子中装有一个几何体模型，两位同学摸该模型并描述它的特征．甲同学：它有4个面是三角形；乙同学：它有8条棱．该模型的形状对应的立体图形可能是(　　)
A．三棱柱 B．四棱柱 C．三棱锥 D．四棱锥
8．已知关于x的一元二次方程有两个相等的实根，则k的值为（ ）
A． B． C．2或3 D．或
9．下列运算正确的是（　　）
A．（a2）5=a7 B．（x﹣1）2=x2﹣1
C．3a2b﹣3ab2=3 D．a2•a4=a6
10．如图所示的几何体的俯视图是（    ）

A． B． C． D．
二、填空题（共7小题，每小题3分，满分21分）
11．当a＜0，b＞0时．化简：＝_____．
12．一个n边形的内角和为1080°，则n=________.
13．如图，四边形ABCD中，E，F，G，H分别是边AB、BC、CD、DA的中点．若四边形EFGH为菱形，则对角线AC、BD应满足条件_____．

14．可燃冰是一种新型能源，它的密度很小，可燃冰的质量仅为.数字0.00092用科学记数法表示是__________．
15．某商品每件标价为150元，若按标价打8折后，再降价10元销售，仍获利10％，则该商品每件的进价为_________元．
16．2017年12月31日晚，郑东新区如意湖文化广场举行了“文化跨年夜、出彩郑州人”的跨年庆祝活动，大学生小明和小刚都各自前往观看了演出，而且他们两人前往时选择了以下三种交通工具中的一种：共享单车、公交、地铁，则他们两人选择同一种交通工具前往观看演出的概率为_____．
17．如图，矩形ABCD中，AB=4，BC=8，P，Q分别是直线BC，AB上的两个动点，AE=2，△AEQ沿EQ翻折形成△FEQ，连接PF，PD，则PF+PD的最小值是____．

三、解答题（共7小题，满分69分）
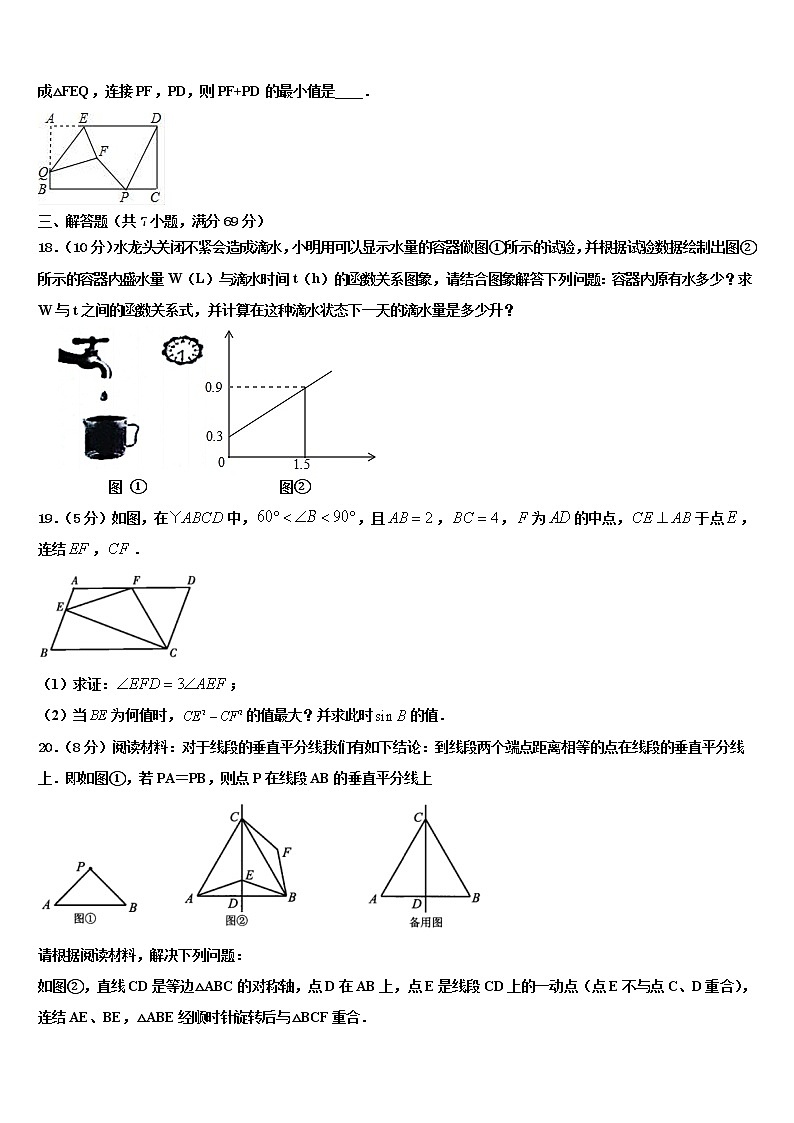
18．（10分）水龙头关闭不紧会造成滴水，小明用可以显示水量的容器做图①所示的试验，并根据试验数据绘制出图②所示的容器内盛水量W（L）与滴水时间t（h）的函数关系图象，请结合图象解答下列问题：容器内原有水多少？求W与t之间的函数关系式，并计算在这种滴水状态下一天的滴水量是多少升？

图 ① 图②
19．（5分）如图，在中，，且，，为的中点，于点，连结，．

（1）求证：；
（2）当为何值时，的值最大？并求此时的值．
20．（8分）阅读材料：对于线段的垂直平分线我们有如下结论：到线段两个端点距离相等的点在线段的垂直平分线上．即如图①，若PA＝PB，则点P在线段AB的垂直平分线上

请根据阅读材料，解决下列问题：
如图②，直线CD是等边△ABC的对称轴，点D在AB上，点E是线段CD上的一动点（点E不与点C、D重合），连结AE、BE，△ABE经顺时针旋转后与△BCF重合．
（I）旋转中心是点 ，旋转了 （度）；
（II）当点E从点D向点C移动时，连结AF，设AF与CD交于点P，在图②中将图形补全，并探究∠APC的大小是否保持不变？若不变，请求出∠APC的度数；若改变，请说出变化情况．
21．（10分）在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同的速度在直线DC，CB上移动．
（1）如图1，当点E在边DC上自D向C移动，同时点F在边CB上自C向B移动时，连接AE和DF交于点P，请你写出AE与DF的数量关系和位置关系，并说明理由；
（2）如图2，当E，F分别在边CD，BC的延长线上移动时，连接AE，DF，（1）中的结论还成立吗？（请你直接回答“是”或“否”，不需证明）；连接AC，请你直接写出△ACE为等腰三角形时CE：CD的值；
（3）如图3，当E，F分别在直线DC，CB上移动时，连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动，请你画出点P运动路径的草图．若AD＝2，试求出线段CP的最大值．

22．（10分）为了巩固全国文明城市建设成果，突出城市品质的提升，近年来，某市积极落实节能减排政策，推行绿色建筑，据统计，该市2014年的绿色建筑面积约为950万平方米，2016年达到了1862万平方米．若2015年、2016年的绿色建筑面积按相同的增长率逐年递增，请解答下列问题：求这两年该市推行绿色建筑面积的年平均增长率；2017年该市计划推行绿色建筑面积达到2400万平方米．如果2017年仍保持相同的年平均增长率，请你预测2017年该市能否完成计划目标.
23．（12分）如图，抛物线y=﹣x2+bx+c（a≠0）与x轴交于点A（﹣1，0）和B（3，0），与y轴交于点C，点D的横坐标为m（0＜m＜3），连结DC并延长至E，使得CE=CD，连结BE，BC．
（1）求抛物线的解析式；
（2）用含m的代数式表示点E的坐标，并求出点E纵坐标的范围；
（3）求△BCE的面积最大值．

24．（14分）有4张正面分别标有数字﹣1，2，﹣3，4的不透明卡片，它们除数字外其余全部相同，现将它们背面朝上，洗匀后从4张卡片中随机摸出一张不放回，将该卡片上的数字记为m，在随机抽取1张，将卡片的数字即为n．
（1）请用列表或树状图的方式把（m，n）所有的结果表示出来．
（2）求选出的（m，n）在二、四象限的概率．



参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、A
【解析】
直接利用相似三角形的判定与性质得出△ONC1三边关系，再利用勾股定理得出答案．
【详解】
过点C1作C1N⊥x轴于点N，过点A1作A1M⊥x轴于点M，

由题意可得：∠C1NO=∠A1MO=90°，
∠1=∠2=∠1，
则△A1OM∽△OC1N，
∵OA=5，OC=1，
∴OA1=5，A1M=1，
∴OM=4，
∴设NO=1x，则NC1=4x，OC1=1，
则（1x）2+（4x）2=9，
解得：x=±（负数舍去），
则NO=，NC1=，
故点C的对应点C1的坐标为：（-，）．
故选A．
【点睛】
此题主要考查了矩形的性质以及勾股定理等知识，正确得出△A1OM∽△OC1N是解题关键．
2、B
【解析】
分析：列举出所有情况，看各路口都是绿灯的情况占总情况的多少即可．
详解：画树状图，得

∴共有8种情况，经过每个路口都是绿灯的有一种，
∴实际这样的机会是.
故选B．
点睛：此题考查了树状图法求概率，树状图法适用于三步或三步以上完成的事件，解题时要注意列出所有的情形．用到的知识点为：概率=所求情况数与总情况数之比．
3、D
【解析】
相反数的定义是：如果两个数只有符号不同，我们称其中一个数为另一个数的相反数，特别地，1的相反数还是1．
【详解】
根据相反数的定义可得：－3的相反数是3.故选D.
【点睛】
本题考查相反数，题目简单，熟记定义是关键.
4、B
【解析】
解方程得：x=5或x=1．
当x=1时，3+4=1，不能组成三角形；
当x=5时，3+4＞5，三边能够组成三角形．
∴该三角形的周长为3+4+5=12，
故选B．
5、B
【解析】
试题解析：由题意得，
解得：．
故选B．
6、C
【解析】
根据近似数的精确度：近似数5.0×102精确到十位．
故选C．
考点：近似数和有效数字
7、D
【解析】
试题分析：根据有四个三角形的面，且有8条棱，可知是四棱锥.而三棱柱有两个三角形的面，四棱柱没有三角形的面，三棱锥有四个三角形的面，但是只有6条棱.
故选D
考点：几何体的形状
8、A
【解析】
根据方程有两个相等的实数根结合根的判别式即可得出关于k的方程，解之即可得出结论．
【详解】
∵方程有两个相等的实根，
∴△=k2-4×2×3=k2-24=0，
解得：k=．
故选A．
【点睛】
本题考查了根的判别式，熟练掌握“当△=0时，方程有两个相等的两个实数根”是解题的关键．
9、D
【解析】
根据幂的乘方法则：底数不变，指数相乘；完全平方公式：（a±b）2=a2±2ab+b2；合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变；同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加分别进行计算即可．
【详解】
A、（a2）5=a10，故原题计算错误；
B、（x﹣1）2=x2﹣2x+1，故原题计算错误；
C、3a2b和3ab2不是同类项，不能合并，故原题计算错误；
D、a2•a4=a6，故原题计算正确；
故选：D．
【点睛】
此题主要考查了幂的乘方、完全平方公式、合并同类项和同底数幂的乘法，关键是掌握各计算法则．
10、B
【解析】
根据俯视图是从上往下看得到的图形解答即可.
【详解】
从上往下看得到的图形是：

故选B.
【点睛】
本题考查三视图的知识，解决此类图的关键是由三视图得到相应的立体图形.从正面看到的图是正视图，从上面看到的图形是俯视图，从左面看到的图形是左视图，能看到的线画实线，被遮挡的线画虚线

二、填空题（共7小题，每小题3分，满分21分）
11、
【解析】
分析：按照二次根式的相关运算法则和性质进行计算即可.
详解：
∵，
∴.
故答案为：.
点睛：熟记二次根式的以下性质是解答本题的关键：（1）；（2）=.
12、1
【解析】
直接根据内角和公式计算即可求解.
【详解】
（n﹣2）•110°=1010°，解得n=1．
故答案为1．
【点睛】
主要考查了多边形的内角和公式.多边形内角和公式：.
13、AC=BD．
【解析】
试题分析：添加的条件应为：AC=BD，把AC=BD作为已知条件，根据三角形的中位线定理可得，HG平行且等于AC的一半，EF平行且等于AC的一半，根据等量代换和平行于同一条直线的两直线平行，得到HG和EF平行且相等，所以EFGH为平行四边形，又EH等于BD的一半且AC=BD，所以得到所证四边形的邻边EH与HG相等，所以四边形EFGH为菱形．
试题解析：添加的条件应为：AC=BD．
证明：∵E，F，G，H分别是边AB、BC、CD、DA的中点，
∴在△ADC中，HG为△ADC的中位线，所以HG∥AC且HG=AC；同理EF∥AC且EF=AC，同理可得EH=BD，
则HG∥EF且HG=EF，
∴四边形EFGH为平行四边形，又AC=BD，所以EF=EH，
∴四边形EFGH为菱形．
考点：1．菱形的性质；2．三角形中位线定理．
14、9.2×10﹣1．
【解析】
根据科学记数法的正确表示为,由题意可得0.00092用科学记数法表示是9.2×10﹣1.
【详解】
根据科学记数法的正确表示形式可得:
0.00092用科学记数法表示是9.2×10﹣1.
故答案为: 9.2×10﹣1.
【点睛】
本题主要考查科学记数法的正确表现形式,解决本题的关键是要熟练掌握科学记数法的正确表现形式.
15、1
【解析】
试题分析：设该商品每件的进价为x元，则
150×80%－10－x＝x×10%，
解得 x＝1．
即该商品每件的进价为1元．
故答案为1．
点睛：此题主要考查了一元一次方程的应用，解决本题的关键是得到商品售价的等量关系．
16、
【解析】
首先根据题意画树状图，然后根据树状图即可求得所有等可能的结果，最后用概率公式求解即可求得答案．
【详解】
树状图如图所示，

∴一共有9种等可能的结果；
根据树状图知，两人选择同一种交通工具前往观看演出的有3种情况，
∴选择同一种交通工具前往观看演出的概率：，
故答案为．
【点睛】
此题考查了树状图法求概率．注意树状图法适合两步或两步以上完成的事件，树状图法可以不重不漏的表示出所有等可能的结果，用到的知识点为：概率=所求情况数与总情况数之比．
17、1
【解析】
如图作点D关于BC的对称点D′，连接PD′，ED′，由DP=PD′，推出PD+PF=PD′+PF，又EF=EA=2是定值，即可推出当E、F、P、D′共线时，PF+PD′定值最小，最小值=ED′﹣EF．
【详解】
如图作点D关于BC的对称点D′，连接PD′，ED′，
在Rt△EDD′中，∵DE=6，DD′=1，
∴ED′==10，
∵DP=PD′，
∴PD+PF=PD′+PF，
∵EF=EA=2是定值，
∴当E、F、P、D′共线时，PF+PD′定值最小，最小值=10﹣2=1，
∴PF+PD的最小值为1，
故答案为1．

【点睛】
本题考查翻折变换、矩形的性质、勾股定理等知识，解题的关键是学会利用轴对称，根据两点之间线段最短解决最短问题.

三、解答题（共7小题，满分69分）
18、（1）0.3 L；（2）在这种滴水状态下一天的滴水量为9.6 L.
【解析】
（1）根据点的实际意义可得；
（2）设与之间的函数关系式为，待定系数法求解可得，计算出时的值，再减去容器内原有的水量即可.
【详解】
（1）由图象可知，容器内原有水0.3 L.
（2）由图象可知W与t之间的函数图象经过点（0，0.3），
故设函数关系式为W＝kt＋0.3.
又因为函数图象经过点（1.5，0.9），
代入函数关系式，得1.5k＋0.3＝0.9，解得k＝0.4.
故W与t之间的函数关系式为W＝0.4t＋0.3.
当t＝24时，W＝0.4×24＋0.3＝9.9（L），9.9－0.3＝9.6（L），
即在这种滴水状态下一天的滴水量为9.6 L.
【点睛】
本题考查了一次函数的应用，关键是利用待定系数法正确求出一次函数的解析式.
19、（1）见解析；（2）时，的值最大，
【解析】
（1）延长BA、CF交于点G，利用可证△AFG≌△DFC得出，，根据，可证出，得出，利用，，点是的中点，得出，，则有，可得出，得出，即可得出结论；
（2）设BE=x，则，，由勾股定理得出，，得出，求出，由二次函数的性质得出当x=1，即BE=1时，CE2-CF2有最大值，，由三角函数定义即可得出结果．
【详解】
解：（1）证明：如图，延长交的延长线于点，

∵为的中点，
∴．
在中，，
∴．
在和中，

∴，
∴，，
∵．
∴，
∴，
∵，，点是的中点，
∴，．
∴．
∴．
∴．
在中，，
又∵，
∴．
∴
（2）设，则，
∵，
∴，
在中，，
在中，，
∵，
∴，
∴，
∴当，即时，的值最大，
∴．
在中，
【点睛】
本题考查了平行四边形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、等腰三角形的判定与性质等知识；证明三角形全等和等腰三角形是解题的关键．
20、B 60
【解析】
分析：(1)根据旋转的性质可得出结论;(2)根据旋转的性质可得BF=CF，则点F在线段BC的垂直平分线上，又由AC=AB，可得点A在线段BC的垂直平分线上，由AF垂直平分BC,即∠CQP=90，进而得出∠APC的度数.
详解：(1)B,60；
（2）补全图形如图所示；

的大小保持不变,
理由如下：设与交于点
∵直线是等边的对称轴
∴,
∵经顺时针旋转后与重合
∴ ,
∴
∴点在线段的垂直平分线上
∵
∴点在线段的垂直平分线上
∴垂直平分,即
∴
点睛：本题考查了旋转的性质，解题的关键是熟记旋转的性质及垂直平分线的性质，注意只证明一点是不能说明这条直线是垂直平分线的.
21、（1）AE=DF，AE⊥DF，理由见解析；（2）成立，CE:CD=或2；（3）
【解析】
试题分析：（1）根据正方形的性质，由SAS先证得△ADE≌△DCF．由全等三角形的性质得AE=DF，∠DAE=∠CDF，再由等角的余角相等可得AE⊥DF；
（2）有两种情况：①当AC=CE时，设正方形ABCD的边长为a，由勾股定理求出AC=CE=a即可；②当AE=AC时，设正方形的边长为a，由勾股定理求出AC=AE=a，根据正方形的性质知∠ADC=90°，然后根据等腰三角形的性质得出DE=CD=a即可；
（3）由（1）（2）知：点P的路径是一段以AD为直径的圆，设AD的中点为Q，连接QC交弧于点P，此时CP的长度最大，再由勾股定理可得QC的长，再求CP即可．
试题解析：（1）AE=DF，AE⊥DF，
理由是：∵四边形ABCD是正方形，
∴AD=DC，∠ADE=∠DCF=90°，
∵动点E，F分别从D，C两点同时出发，以相同的速度在直线DC，CB上移动，
∴DE=CF，
在△ADE和△DCF中
，
∴，
∴AE=DF，∠DAE=∠FDC，
∵∠ADE=90°，∴∠ADP+∠CDF=90°，
∴∠ADP+∠DAE=90°，
∴∠APD=180°-90°=90°，
∴AE⊥DF；
（2）（1）中的结论还成立，
有两种情况：

①如图1，当AC=CE时，
设正方形ABCD的边长为a，由勾股定理得，
，
则；

②如图2，当AE=AC时，
设正方形ABCD的边长为a，由勾股定理得：
，
∵四边形ABCD是正方形，
∴∠ADC=90°，即AD⊥CE，
∴DE=CD=a，
∴CE:CD=2a:a=2；

即CE:CD=或2；
（3）∵点P在运动中保持∠APD=90°，
∴点P的路径是以AD为直径的圆，
如图3，设AD的中点为Q，连接CQ并延长交圆弧于点P，
此时CP的长度最大，
∵在Rt△QDC中，
∴，
即线段CP的最大值是.
点睛：此题主要考查了正方形的性质，勾股定理，圆周角定理，全等三角形的性质与判定，等腰三角形的性质，三角形的内角和定理，能综合运用性质进行推挤是解此题的关键，用了分类讨论思想，难度偏大.
22、（1）这两年该市推行绿色建筑面积的年平均增长率为40%；（2）如果2017年仍保持相同的年平均增长率，2017年该市能完成计划目标．
【解析】
试题分析：（1）设这两年该市推行绿色建筑面积的年平均增长率x，根据2014年的绿色建筑面积约为700万平方米和2016年达到了1183万平方米，列出方程求解即可；
（2）根据（1）求出的增长率问题，先求出预测2017年绿色建筑面积，再与计划推行绿色建筑面积达到1500万平方米进行比较，即可得出答案．
试题解析：（1）设这两年该市推行绿色建筑面积的年平均增长率为x，
根据题意得：700（1+x）2=1183，
解得：x1=0.3=30%，x2=﹣2.3（舍去），
答：这两年该市推行绿色建筑面积的年平均增长率为30%；
（2）根据题意得：1183×（1+30%）=1537.9（万平方米），
∵1537.9＞1500，
∴2017年该市能完成计划目标．
【点睛】本题考查了一元二次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件和增长率问题的数量关系，列出方程进行求解．
23、（1）y=﹣x2+2x+1．（2）2≤Ey＜2．（1）当m=1.5时，S△BCE有最大值，S△BCE的最大值=．
【解析】
分析：(1) 1)把A、B两点代入抛物线解析式即可;(2)设，利用求线段中点的公式列出关于m的方程组，再利用0＜m＜1即可求解;(1) 连结BD，过点D作x轴的垂线交BC于点H,由，设出点D的坐标，进而求出点H的坐标，利用三角形的面积公式求出，再利用公式求二次函数的最值即可.
详解：(1)∵抛物线 过点A（1，0）和B（1，0）

（2）∵
∴点C为线段DE中点
设点E（a,b）

∵0＜m＜1,
∴当m=1时，纵坐标最小值为2
当m=1时，最大值为2
∴点E纵坐标的范围为
（1）连结BD，过点D作x轴的垂线交BC于点H
∵CE=CD
∴H（m，-m+1）
∴
当m=1.5时，
.

点睛：本题考查了二次函数的综合题、待定系数法、一次函数等知识点，解题的关键是灵活运用所学知识解决问题，会用方程的思想解决问题.
24、（1）详见解析；（2）P=．
【解析】
试题分析：（1）树状图列举所有结果.(2)用在第二四象限的点数除以所有结果.
试题解析：
(1)画树状图得：
则（m，n）共有12种等可能的结果：（2，-1），（2，﹣3），（2， 4），（-1，2），（-1，﹣3），（1， 4），（﹣3，2），（﹣3，-1），（﹣3， 4），（﹣4，2），（4，-1），（4，﹣3）.
（2）（m，n）在二、四象限的（2，-1），（2，﹣3），（-1，2），（﹣3，2），（﹣3， 4），（﹣4，2），（4，-1），（4，﹣3），
∴所选出的m，n在第二、三四象限的概率为：P==
点睛：（1）利用频率估算法：大量重复试验中，事件A发生的频率会稳定在某个常数p附近，那么这个常数P就叫做事件A的概率（有些时候用计算出A发生的所有频率的平均值作为其概率）.
(2)定义法：如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，考察事件A包含其中的m中结果，那么事件A发生的概率为P.
(3)列表法：当一次试验要设计两个因素，可能出现的结果数目较多时，为不重不漏地列出所有可能的结果，通常采用列表法.其中一个因素作为行标，另一个因素作为列标.
(4)树状图法：当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率.