2022年四川省宜宾市高县中考数学考前最后一卷含解析

这是一份2022年四川省宜宾市高县中考数学考前最后一卷含解析，共22页。试卷主要包含了把直线l等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．统计学校排球队员的年龄，发现有12、13、14、15等四种年龄，统计结果如下表：
年龄（岁）
12
13
14
15
人数（个）
2
4
6
8
根据表中信息可以判断该排球队员年龄的平均数、众数、中位数分别为（ ）
A．13、15、14 B．14、15、14 C．13.5、15、14 D．15、15、15
2．下列运算正确的是（　　）
A．（﹣2a）3=﹣6a3 B．﹣3a2•4a3=﹣12a5
C．﹣3a（2﹣a）=6a﹣3a2 D．2a3﹣a2=2a
3．某中学为了创建“最美校园图书屋”，新购买了一批图书，其中科普类图书平均每本书的价格是文学类图书平均每本书价格的1.2倍．已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本，那么学校购买文学类图书平均每本书的价格是多少元？设学校购买文学类图书平均每本书的价格是x元，则下面所列方程中正确的是（　　）
A． B．
C． D．
4．在一个口袋中有4个完全相同的小球，把它们分别标号为 1，2，3，4，随机地摸出一个小球然后放回，再随机地摸出一个小球．则两次摸出的小球的标号的和等于6的概率为（　　）
A． B． C． D．
5．把直线l：y=kx+b绕着原点旋转180°，再向左平移1个单位长度后，经过点A（-2,0）和点B（0,4），则直线l的表达式是（ ）
A．y=2x+2 B．y=2x-2 C．y=-2x+2 D．y=-2x-2
6．1.在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）
A． B． C． D．
7．如图，中，，，将绕点逆时针旋转得到，使得，延长交于点，则线段的长为（ ）

A．4 B．5 C．6 D．7
8．已知a，b，c在数轴上的位置如图所示，化简|a+c|-|a-2b|-|c+2b|的结果是（ ）

A．4b+2c B．0 C．2c D．2a+2c
9．已知⊙O1与⊙O2的半径分别是3cm和5cm，两圆的圆心距为4cm，则两圆的位置关系是（ ）
A．相交 B．内切 C．外离 D．内含
10．近两年，中国倡导的“一带一路”为沿线国家创造了约180000个就业岗位，将180000用科学记数法表示为（　　）
A．1.8×105 B．1.8×104 C．0.18×106 D．18×104
11．如图，△ABC中，D为BC的中点，以D为圆心，BD长为半径画一弧交AC于E点，若∠A=60°，∠B=100°，BC=4，则扇形BDE的面积为何？（　　）

A． B． C． D．
12．在半径等于5 cm的圆内有长为cm的弦，则此弦所对的圆周角为
A．60° B．120° C．60°或120° D．30°或120°
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．函数中自变量的取值范围是______________
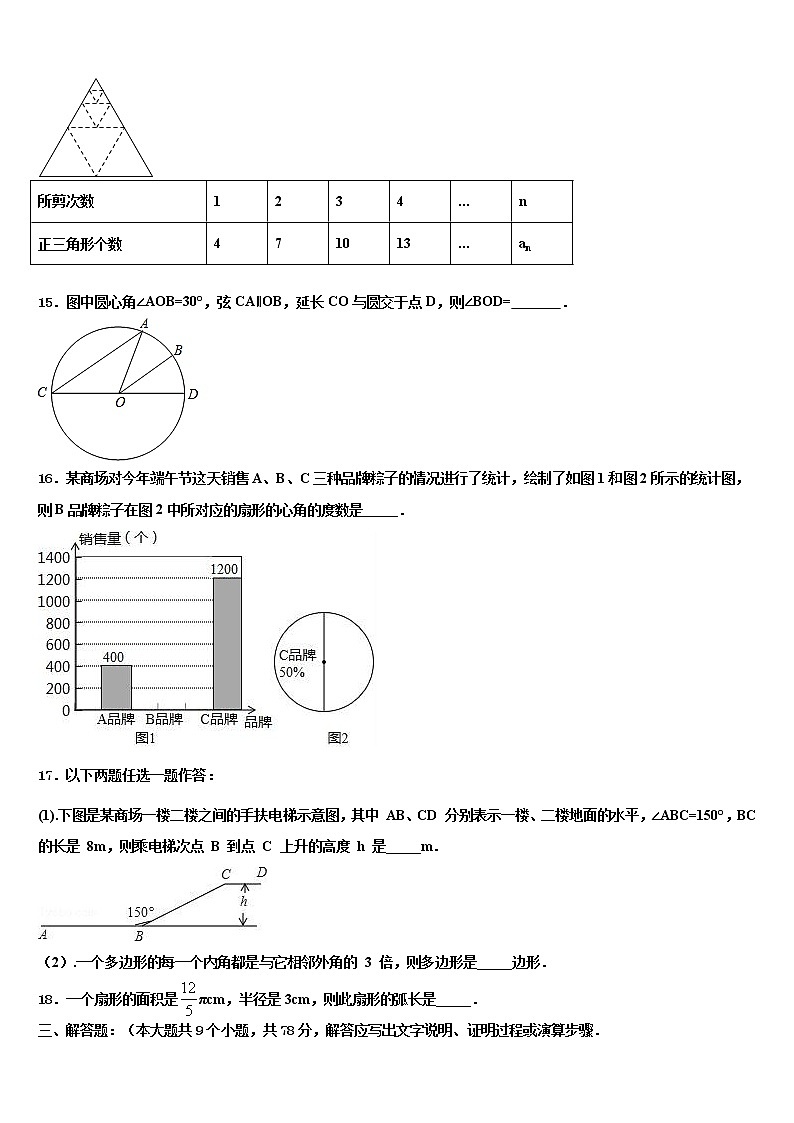
14．如图，将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，……如此继续下去，结果如下表：则an＝__________（用含n的代数式表示）．

所剪次数
1
2
3
4
…
n
正三角形个数
4
7
10
13
…
an

15．图中圆心角∠AOB=30°，弦CA∥OB，延长CO与圆交于点D，则∠BOD= ．

16．某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行了统计，绘制了如图1和图2所示的统计图，则B品牌粽子在图2中所对应的扇形的心角的度数是_____．

17．以下两题任选一题作答：
(1).下图是某商场一楼二楼之间的手扶电梯示意图，其中 AB、CD 分别表示一楼、二楼地面的水平，∠ABC=150°，BC 的长是 8m，则乘电梯次点 B 到点 C 上升的高度 h 是_____m．

（2）.一个多边形的每一个内角都是与它相邻外角的 3 倍，则多边形是_____边形．
18．一个扇形的面积是πcm，半径是3cm，则此扇形的弧长是_____．
三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）的除以20与18的差，商是多少？
20．（6分）如图所示，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB于点D，CD交AE于点F，过C作CG∥AE交BA的延长线于点G．求证：CG是⊙O的切线．求证：AF＝CF．若sinG＝0.6，CF＝4，求GA的长．

21．（6分）如图，AB是⊙O的直径，D、D为⊙O上两点，CF⊥AB于点F，CE⊥AD交AD的延长线于点E，且CE=CF.
（1）求证：CE是⊙O的切线；
（2）连接CD、CB，若AD=CD=a，求四边形ABCD面积.

22．（8分）如图，已知点A，B，C在半径为4的⊙O上，过点C作⊙O的切线交OA的延长线于点D．
（Ⅰ）若∠ABC=29°，求∠D的大小；
（Ⅱ）若∠D=30°，∠BAO=15°，作CE⊥AB于点E，求：
①BE的长；
②四边形ABCD的面积．

23．（8分）计算：（﹣1）2﹣2sin45°+（π﹣2018）0+|﹣|
24．（10分）如图，AB是⊙O的直径，点C是AB延长线上的点，CD与⊙O相切于点D，连结BD、AD．
（1）求证；∠BDC＝∠A．
（2）若∠C＝45°，⊙O的半径为1，直接写出AC的长．

25．（10分）如图1，△ABC与△CDE都是等腰直角三角形，直角边AC，CD在同一条直线上，点M、N分别是斜边AB、DE的中点，点P为AD的中点，连接AE，BD，PM，PN，MN．
（1）观察猜想：
图1中，PM与PN的数量关系是　 　，位置关系是　 　．
（2）探究证明：
将图1中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图2，AE与MP、BD分别交于点G、H，判断△PMN的形状，并说明理由；
（3）拓展延伸：
把△CDE绕点C任意旋转，若AC=4，CD=2，请直接写出△PMN面积的最大值．

26．（12分）某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图．

请结合以上信息解答下列问题：m=　 　；请补全上面的条形统计图；在图2中，“乒乓球”所对应扇形的圆心角的度数为　 　；已知该校共有1200名学生，请你估计该校约有　 　名学生最喜爱足球活动．
27．（12分）元旦放假期间，小明和小华准备到西安的大雁塔（记为A）、白鹿原（记为B）、兴庆公园（记为C）、秦岭国家植物园（记为D）中的一个景点去游玩，他们各自在这四个景点中任选一个，每个景点被选中的可能性相同．
（1）求小明选择去白鹿原游玩的概率；
（2）用树状图或列表的方法求小明和小华都选择去秦岭国家植物园游玩的概率．



参考答案

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、B
【解析】
根据加权平均数、众数、中位数的计算方法求解即可.
【详解】
，
15出现了8次，出现的次数最多，故众数是15，
从小到大排列后，排在10、11两个位置的数是14，14，故中位数是14.
故选B.
【点睛】
本题考查了平均数、众数与中位数的意义．数据x1、x2、……、xn的加权平均数：（其中w1、w2、……、wn分别为x1、x2、……、xn的权数）.一组数据中出现次数最多的数据叫做众数．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数），叫做这组数据的中位数．
2、B
【解析】
先根据同底数幂的乘法法则进行运算即可。
【详解】
A.;故本选项错误;
B. ﹣3a2•4a3=﹣12a5; 故本选项正确;
C.;故本选项错误;
D. 不是同类项不能合并; 故本选项错误;
故选B.
【点睛】
先根据同底数幂的乘法法则, 幂的乘方, 积的乘方, 合并同类项分别求出每个式子的值, 再判断即可.
3、B
【解析】
首先设文学类图书平均每本的价格为x元，则科普类图书平均每本的价格为1.2x元，根据题意可得等量关系：学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本，根据等量关系列出方程，
【详解】
设学校购买文学类图书平均每本书的价格是x元，可得：
故选B．
【点睛】
此题主要考查了分式方程的应用，关键是正确理解题意，找出题目中的等量关系，列出方程．
4、C
【解析】
列举出所有情况，看两次摸出的小球的标号的和等于6的情况数占总情况数的多少即可．
解：

共16种情况，和为6的情况数有3种，所以概率为．
故选C．
5、B
【解析】
先利用待定系数法求出直线AB的解析式，再求出将直线AB向右平移1个单位长度后得到的解析式，然后将所得解析式绕着原点旋转180°即可得到直线l．
【详解】
解：设直线AB的解析式为y＝mx＋n．
∵A（−2，0），B（0，1），
∴ ，
解得 ，
∴直线AB的解析式为y＝2x＋1．
将直线AB向右平移1个单位长度后得到的解析式为y＝2（x−1）＋1，即y＝2x＋2，
再将y＝2x＋2绕着原点旋转180°后得到的解析式为−y＝−2x＋2，即y＝2x−2，
所以直线l的表达式是y＝2x−2．
故选：B．
【点睛】
本题考查了一次函数图象平移问题，掌握解析式“左加右减”的规律以及关于原点对称的规律是解题的关键．
6、D
【解析】
根据轴对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．
【详解】
A、不是轴对称图形，故A不符合题意；
B、不是轴对称图形，故B不符合题意；
C、不是轴对称图形，故C不符合题意；
D、是轴对称图形，故D符合题意．
故选D.
【点睛】
本题主要考查轴对称图形的知识点．确定轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
7、B
【解析】
先利用已知证明，从而得出，求出BD的长度，最后利用求解即可．
【详解】










故选：B．
【点睛】
本题主要考查相似三角形的判定及性质，掌握相似三角形的性质是解题的关键．
8、A
【解析】
由数轴上点的位置得：b|c|>|a|，
∴a+c>0，a−2b>0，c+2b<0，
则原式=a+c−a+2b+c+2b=4b +2c.
故选：B.
点睛：本题考查了整式的加减以及数轴，涉及的知识有：去括号法则以及合并同类项法则，熟练掌握运算法则是解本题的关键.
9、A
【解析】
试题分析：∵⊙O1和⊙O2的半径分别为5cm和3cm，圆心距O1O2=4cm，5﹣3＜4＜5+3，
∴根据圆心距与半径之间的数量关系可知⊙O1与⊙O2相交．
故选A．
考点：圆与圆的位置关系．
10、A
【解析】
科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．
【详解】
180000=1.8×105，
故选A．
【点睛】
本题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
11、C
【解析】
分析：求出扇形的圆心角以及半径即可解决问题；
详解：∵∠A=60°，∠B=100°，
∴∠C=180°﹣60°﹣100°=20°，
∵DE=DC，
∴∠C=∠DEC=20°，
∴∠BDE=∠C+∠DEC=40°，
∴S扇形DBE=．
故选C．
点睛：本题考查扇形的面积公式、三角形内角和定理等知识，解题的关键是记住扇形的面积公式：S=．
12、C
【解析】
根据题意画出相应的图形，由OD⊥AB，利用垂径定理得到D为AB的中点，由AB的长求出AD与BD的长，且得出OD为角平分线，在Rt△AOD中，利用锐角三角函数定义及特殊角的三角函数值求出∠AOD的度数，进而确定出∠AOB的度数，利用同弧所对的圆心角等于所对圆周角的2倍，即可求出弦AB所对圆周角的度数．
【详解】
如图所示，

∵OD⊥AB，
∴D为AB的中点，即AD=BD=，
在Rt△AOD中，OA=5，AD=，
∴sin∠AOD=，
又∵∠AOD为锐角，
∴∠AOD=60°，
∴∠AOB=120°，
∴∠ACB=∠AOB=60°，
又∵圆内接四边形AEBC对角互补，
∴∠AEB=120°，
则此弦所对的圆周角为60°或120°．
故选C．
【点睛】
此题考查了垂径定理，圆周角定理，特殊角的三角函数值，以及锐角三角函数定义，熟练掌握垂径定理是解本题的关键．

二、填空题：（本大题共6个小题，每小题4分，共24分．）
13、x≤2且x≠1
【解析】
解：根据题意得：
且x−1≠0，
解得：且
故答案为且
14、3n+1．
【解析】
试题分析：从表格中的数据，不难发现：多剪一次，多3个三角形．即剪n次时，共有4+3（n-1）=3n+1．
试题解析：故剪n次时，共有4+3（n-1）=3n+1．
考点：规律型：图形的变化类．
15、30°
【解析】
试题分析：∵CA∥OB，∠AOB=30°，∴∠CAO=∠AOB=30°．
∵OA=OC，∴∠C=∠OAC=30°．
∵∠C和∠AOD是同弧所对的圆周角和圆心角，∴∠AOD=2∠C=60°．
∴∠BOD=60°－30°=30°．
16、120°
【解析】
根据图1中C品牌粽子1200个，在图2中占50%，求出三种品牌粽子的总个数，再求出B品牌粽子的个数，从而计算出B品牌粽子占粽子总数的比例，从而求出B品牌粽子在图2中所对应的圆心角的度数．
【详解】
解：∵三种品牌的粽子总数为1200÷50%=2400个，
又∵A、C品牌的粽子分别有400个、1200个，
∴B品牌的粽子有2400-400-1200=800个，
则B品牌粽子在图2中所对应的圆心角的度数为360×．
故答案为120°．
【点睛】
本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
17、4 8
【解析】
（1）先求出斜边的坡角为30°，再利用含30°的直角三角形即可求解；
（2）设这个多边形边上为n，则内角和为（n-2）×180°，外角度数为
故可列出方程求解.
【详解】
（1）∵∠ABC=150°，∴斜面BC的坡角为30°，
∴h==4m
（2）设这个多边形边上为n，则内角和为（n-2）×180°，外角度数为
依题意得
解得n=8
故为八边形.
【点睛】
此题主要考查含30°的直角三角形与多边形的内角和计算，解题的关键是熟知含30°的直角三角形的性质与多边形的内角和公式.
18、
【解析】
根据扇形面积公式求解即可
【详解】
根据扇形面积公式.
可得：，
，
故答案：.
【点睛】
本题主要考查了扇形的面积和弧长之间的关系, 利用扇形弧长和半径代入公式即可求解, 正确理解公式是解题的关键. 注意在求扇形面积时, 要根据条件选择扇形面积公式.

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、
【解析】
根据题意可用乘的积除以20与18的差，所得的商就是所求的数，列式解答即可．
【详解】
解：×÷（20﹣18）
【点睛】
考查有理数的混合运算，列出式子是解题的关键.
20、（1）见解析；（2）见解析；（3）AG＝1．
【解析】
（1）利用垂径定理、平行的性质，得出OC⊥CG，得证CG是⊙O的切线.
（2）利用直径所对圆周角为和垂直的条件得出∠2=∠B，再根据等弧所对的圆周角相等得出∠1=∠B，进而证得∠1=∠2，得证AF=CF.
（3）根据直角三角形的性质，求出AD的长度，再利用平行的性质计算出结果.
【详解】
（1）证明：连结OC，如图，
∵C是劣弧AE的中点，
∴OC⊥AE，
∵CG∥AE，
∴CG⊥OC，
∴CG是⊙O的切线；
（2）证明：连结AC、BC，
∵AB是⊙O的直径，
∴∠ACB＝90°，
∴∠2+∠BCD＝90°，
而CD⊥AB，
∴∠B+∠BCD＝90°，
∴∠B＝∠2，
∵C是劣弧AE的中点，
∴,
∴∠1＝∠B，
∴∠1＝∠2，
∴AF＝CF；
（3）解：∵CG∥AE，
∴∠FAD＝∠G，
∵sinG＝0.6，
∴sin∠FAD＝＝0.6，
∵∠CDA＝90°，AF＝CF＝4，
∴DF＝2.4，
∴AD＝3.2，
∴CD＝CF+DF＝6.4，
∵AF∥CG，
∴,
∴
∴DG＝，
∴AG＝DG﹣AD＝1．

【点睛】
本题主要考查与圆有关的位置关系和圆中的计算问题,掌握切线的判定定理以及解直角三角形是解题的关键.
21、（1）证明见解析；（2）
【解析】
（1）连接OC，AC，可先证明AC平分∠BAE，结合圆的性质可证明OC∥AE，可得∠OCB＝90°，可证得结论；
（2）可先证得四边形AOCD为平行四边形，再证明△OCB为等边三角形，可求得CF、AB，利用梯形的面积公式可求得答案．
【详解】
（1）证明：连接OC，AC．
∵CF⊥AB，CE⊥AD，且CE＝CF．
∴∠CAE＝∠CAB．
∵OC＝OA，
∴∠CAB＝∠OCA．
∴∠CAE＝∠OCA．
∴OC∥AE．
∴∠OCE＋∠AEC＝180°，
∵∠AEC＝90°，
∴∠OCE＝90°即OC⊥CE，
∵OC是⊙O的半径，点C为半径外端，
∴CE是⊙O的切线．
（2）解：∵AD＝CD，
∴∠DAC＝∠DCA＝∠CAB，
∴DC∥AB，
∵∠CAE＝∠OCA，
∴OC∥AD，
∴四边形AOCD是平行四边形，
∴OC＝AD＝a，AB＝2a，
∵∠CAE＝∠CAB，
∴CD＝CB＝a，
∴CB＝OC＝OB，
∴△OCB是等边三角形，
在Rt△CFB中，CF＝ ，
∴S四边形ABCD＝ （DC＋AB）•CF＝
【点睛】
本题主要考查切线的判定，掌握切线的两种判定方法是解题的关键，即有切点时连接圆心和切点，然后证明垂直，没有切点时，过圆心作垂直，证明圆心到直线的距离等于半径．
22、（1）∠D=32°；（2）①BE＝；②
【解析】
（Ⅰ）连接OC, CD为切线，根据切线的性质可得∠OCD=90°，根据圆周角定理可得∠AOC=2∠ABC=29°×2=58°，根据直角三角形的性质可得∠D的大小.
（Ⅱ）①根据∠D=30°，得到∠DOC=60°，根据∠BAO=15°，可以得出∠AOB=150°，进而证明△OBC为等腰直角三角形，根据等腰直角三角形的性质得出
根据圆周角定理得出根据含角的直角三角形的性质即可求出BE的长；
②根据四边形ABCD的面积=S△OBC+S△OCD﹣S△OAB进行计算即可.
【详解】
（Ⅰ）连接OC,
∵CD为切线，
∴OC⊥CD，
∴∠OCD=90°，
∵∠AOC=2∠ABC=29°×2=58°，
∴∠D=90°﹣58°=32°；
（Ⅱ）①连接OB,
在Rt△OCD中，∵∠D=30°，
∴∠DOC=60°，
∵∠BAO=15°，
∴∠OBA=15°，
∴∠AOB=150°，
∴∠OBC=150°﹣60°=90°，
∴△OBC为等腰直角三角形，
∴
∵
在Rt△CBE中，
∴
②作BH⊥OA于H，如图，
∵∠BOH=180°﹣∠AOB=30°，
∴
∴四边形ABCD的面积=S△OBC+S△OCD﹣S△OAB


【点睛】
考查切线的性质，圆周角定理，等腰直角三角形的判定与性质，含角的等腰直角三角形的性质，三角形的面积公式等，题目比较典型，综合性比较强，难度适中．
23、1
【解析】
原式第一项利用乘方法则计算，第二项利用特殊角的三角函数值计算，第三项利用零指数幂法则计算，最后一项利用绝对值的代数意义化简即可得到结果．
【详解】
解：原式=1﹣1×+1+=1﹣+1+=1．
【点睛】
此题考查了含有特殊角的三角函数值的运算，熟练掌握各运算法则是解题的关键.
24、（1）详见解析；（2）1+
【解析】
（1）连接OD，结合切线的性质和直径所对的圆周角性质，利用等量代换求解（2）根据勾股定理先求OC，再求AC.
【详解】
（1）证明：连结．如图，
与相切于点D，


是的直径，
即




（2）解：在中，
.

【点睛】
此题重点考查学生对圆的认识，熟练掌握圆的性质是解题的关键.
25、（1）PM=PN，PM⊥PN（2）等腰直角三角形，理由见解析（3）
【解析】
（1）由等腰直角三角形的性质易证△ACE≌△BCD，由此可得AE=BD，再根据三角形中位线定理即可得到PM=PN，由平行线的性质可得PM⊥PN；
（2）（1）中的结论仍旧成立，由（1）中的证明思路即可证明；
（3）由（2）可知△PMN是等腰直角三角形，PM=BD，推出当BD的值最大时，PM的值最大，△PMN的面积最大，推出当B、C、D共线时，BD的最大值=BC+CD=6，由此即可解决问题；
【详解】
解：（1）PM=PN，PM⊥PN，理由如下：
延长AE交BD于O，

∵△ACB和△ECD是等腰直角三角形，
∴AC=BC，EC=CD，∠ACB=∠ECD=90°．
在△ACE和△BCD中
，
∴△ACE≌△BCD（SAS），
∴AE=BD，∠EAC=∠CBD，
∵∠EAC+∠AEC=90°，∠AEC=∠BEO，
∴∠CBD+∠BEO=90°，
∴∠BOE=90°，即AE⊥BD，
∵点M、N分别是斜边AB、DE的中点，点P为AD的中点，
∴PM=BD，PN=AE，
∴PM=PM，
∵PM∥BD，PN∥AE，AE⊥BD，
∴∠NPD=∠EAC，∠MPA=∠BDC，∠EAC+∠BDC=90°，
∴∠MPA+∠NPC=90°，
∴∠MPN=90°，
即PM⊥PN，
故答案是：PM=PN，PM⊥PN；
（2）如图②中，设AE交BC于O，

∵△ACB和△ECD是等腰直角三角形，
∴AC=BC，EC=CD，
∠ACB=∠ECD=90°，
∴∠ACB+∠BCE=∠ECD+∠BCE，
∴∠ACE=∠BCD，
∴△ACE≌△BCD，
∴AE=BD，∠CAE=∠CBD，
又∵∠AOC=∠BOE，
∠CAE=∠CBD，
∴∠BHO=∠ACO=90°，
∵点P、M、N分别为AD、AB、DE的中点，
∴PM=BD，PM∥BD，
PN=AE，PN∥AE，
∴PM=PN，
∴∠MGE+∠BHA=180°，
∴∠MGE=90°，
∴∠MPN=90°，
∴PM⊥PN；
（3）由（2）可知△PMN是等腰直角三角形，PM=BD，
∴当BD的值最大时，PM的值最大，△PMN的面积最大，
∴当B、C、D共线时，BD的最大值=BC+CD=6，
∴PM=PN=3，
∴△PMN的面积的最大值=×3×3=．
【点睛】
本题考查的是几何变换综合题，熟知等腰直角三角形的判定与性质、全等三角形的判定与性质、三角形中位线定理的运用，解题的关键是正确寻找全等三角形解决问题，学会利用三角形的三边关系解决最值问题，属于中考压轴题．
26、（1）150，（2）36°，（3）1．
【解析】
（1）根据图中信息列式计算即可；
（2）求得“足球“的人数=150×20%=30人，补全上面的条形统计图即可；
（3）360°×乒乓球”所占的百分比即可得到结论；
（4）根据题意计算即可．
【详解】
（1）m=21÷14%=150，
（2）“足球“的人数=150×20%=30人，
补全上面的条形统计图如图所示；
（3）在图2中，“乒乓球”所对应扇形的圆心角的度数为360°×=36°；
（4）1200×20%=1人，
答：估计该校约有1名学生最喜爱足球活动．
故答案为150，36°，1．

【点睛】
本题考查了条形统计图，观察条形统计图、扇形统计图获得有效信息是解题关键．
27、（1）；（2）
【解析】
（1）利用概率公式直接计算即可；
（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与小明和小华都选择去同一个地方游玩的情况，再利用概率公式即可求得答案．
【详解】
（1）∵小明准备到西安的大雁塔（记为A）、白鹿原（记为B）、兴庆公园（记为C）、秦岭国家植物园（记为D）中的一个景点去游玩，
∴小明选择去白鹿原游玩的概率＝；
（2）画树状图分析如下：

两人选择的方案共有16种等可能的结果，其中选择同种方案有1种，
所以小明和小华都选择去秦岭国家植物园游玩的概率＝．
【点睛】
本题考查了列表法与树状图法：利用列表法和树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，求出概率．