小学数学北师大版五年级下册四 长方体（二）长方体的体积教案配套ppt课件

这是一份小学数学北师大版五年级下册四 长方体（二）长方体的体积教案配套ppt课件，共60页。PPT课件主要包含了知识回顾，Ⅰ课堂导入，II经典例题点拨，III课堂检测，IV课后作业，经典例题等内容，欢迎下载使用。

1.在下面的（ ）中填上合适的体积单位 。
（1）一台冰箱的体积大约是650（ ）。（2）牙膏盒的体积大约是60（ ）。（3）储物柜的体积约是120（ ）。（4）一颗蚕豆的体积大约是 1（ ）。（5）一小瓶牛奶的约有250（ ）。
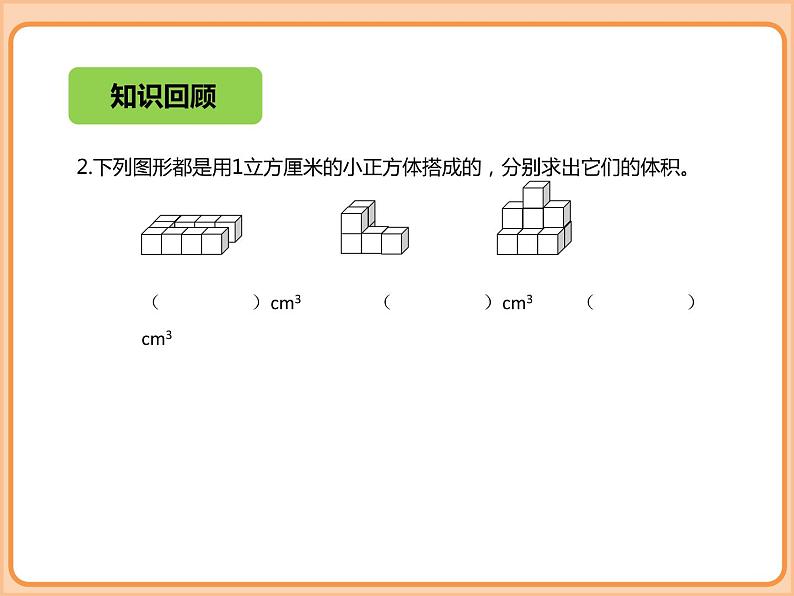
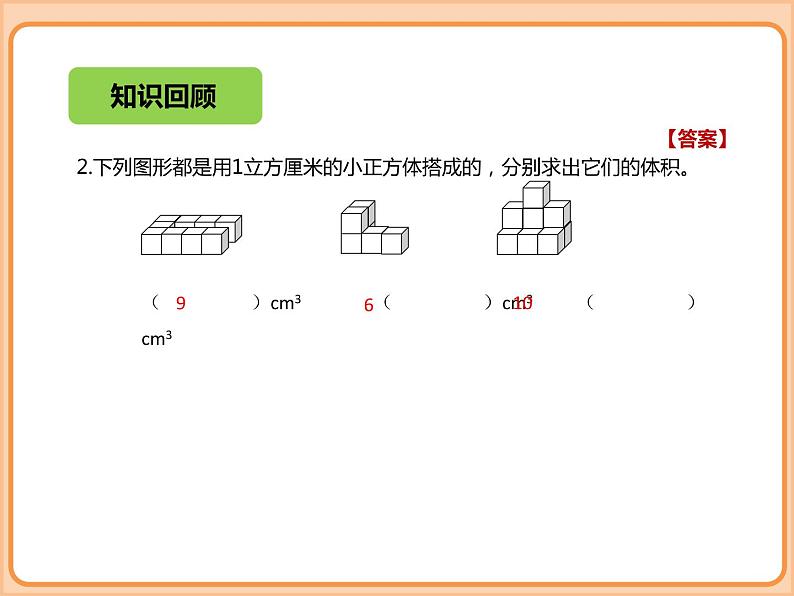
2.下列图形都是用1立方厘米的小正方体搭成的，分别求出它们的体积。
（ ）cm3 （ ）cm3 （ ）cm3
1.掌握长方体、正方体体积的计算方法。 2.能正确计算长方体、正方体的体积，解决一些简答的实际问题。 3.在观察、操作探究的过程中提高动手操作能力，进一步发展空间概念。
【学习重点】 理解长方体和正方体的体积的计算方法；【学习难点】 理解长方体和正方体体积计算公式的推导过程。
怎么知道一个长方体的体积呢？
方法一：切割法把这个长方体切割成棱长是1cm的小正方体块，数一数能切成多少块，它的体积就是多少立方厘米。
缺点：操作复杂，会毁坏被测物体，不能普遍使用。
方法二：测量法先分别测量出长方体的长、宽、高各是多少厘米，然后推算出长方体中包含多少个棱长是1cm的小正方体，最后求出体积。
优点：简便易行，用这个方法可以测量出所有长方体的体积。
探究长方体的体积公式。
用12个体积为1cm3的小正方体摆成不同的长方体，如下图：
数一数，每个长方体的长、宽、高分别是多少厘米？完成下表。
根据拼摆的形状，得出下表。
每个长方体都是由12个小正方体组成的，体积都是12立方厘米，但他们的长、宽、高是不同的。
①通过拼摆发现，每排小正方体的个数相当于长方体的长，排数相当于宽，层数相当于高。②长方体所含小正方体的个数就是长方体的体积数值。③小正方体的数量=长的数值×宽的数值×高的数值，
总结长方体的体积公式。
长方体的体积=长×宽×高；用字母V表示体积：V=abh。
计算下列图形的体积（单位：cm）。
（1） V=10×6×5=300（cm3）（2） V=6×5×4=120（cm3）
一个长方体，长4米，宽3米，高2.4米，它的占地面积最大是多少平方米?表面积是多少？体积是多少立方米？
一个长方体，长4米，宽3米，高2.4米，它的占地面积最大是多少平方米?表面积是多少？ 体积是多少立方米？
占地面积：4×3=12（m2）表面积：2×（4×3+4×2.4+3×2.4）=57.6（m2）体积：4×3×2.4=28.8（m3）答：它的占地面积是12平方米，表面积是57.6平方米，体积是28.8平方米。
长方体的体积公式V=长×宽×高 =abh
正方体是特殊的长方体。
根据长方体与正方体的关系，你能推出正方体的体积是怎样计算的吗？
探究正方体的体积公式。
长方体的体积= 长 × 宽 × 高正方体的体积=棱长×棱长×棱长用字母表示：V= a.a.a = a3 ,a3读作a的立方，表示3个a相乘。
一个正方体的棱长是12厘米，它的体积是多少？
V= 12×12×12=1728（立方厘米）答：它的体积是1728立方厘米。
一块正方体的石料，棱长是8分米，这块石料的体积是多少立方米？如果1立方米的石料重3千克，这块石料重多少千克？
8分米=0.8米0.8×0.8×0.8=0.512（平方米）0.512×3=1.536（千克）答：这块石料重1.536千克。
看清单位！统一后再按相应的关系计算。
正方体体积V= 棱长×棱长×棱长=a3;
计算下列阴影部分的面积和体积。
（1）阴影部分的面积=5×3=15 V=5×3×4=60
（2）阴影部分的面积=3×3=9 V=3×3×3=27
上面长方体、正方体中涂色的面积是各个图形底面的面积，称为底面积底面积S=长×宽。
长方体的体积= 长 × 宽 × 高正方体的体积=棱长×棱长×棱长
长方体或正方体的体积=底面积×高 V=S.h
V表示体积，S表示底面积h表示高。
长方体和正方体体积的同一计算公式。
计算下面图形的体积。
（1） （2）
（1）V=S.h=220×8 =1760（cm3）
（2）V=a3=9×9×9 =729（cm3）
由V= Sh 推出：S=V÷h、h=V÷S
体积统一计算公式：V=底面积×高=S.h底面积S=V÷h高h=V÷S
（1）一个长8cm，宽4cm，高2cm的长方体。它的占地面积最少是（ ）cm²，体积是（ ）   cm³。（2）一个长方体的横截面是边长为3cm的正方形，它的长是5cm，体积是（ ）cm³。（3）一块长方体的橡皮，长是5厘米，宽是4里面，高是3厘米，它的体积是（ ）立方厘米。（4）一个正方体的棱长是9厘米，它的棱长之和是（      ）厘米，表面积是（        ）平方厘米，体积是（ ）立方厘米。
一个正方体的纸箱子体积是64dm³，它的表面积是多少dm²？
体积：64dm³可知该正方体的棱长是4dm。表面积S=4×4×6=96（dm²）答：它的表面积是96dm²。
把一块长方体的钢材，熔铸成一块正方体的钢材，钢材的体积发生了怎样的变化？
体积不会发生改变，因为把一块长方体的钢材熔铸成一块正方体钢材，虽然形状发生了变化，但是钢材所占的空间的大小并没有改变，因此体积也不会变。
一个长方体蓄水池，从里面量长是8米，高5米，深1.2米，蓄水池存满水时，池中有水多少立方米？
求蓄水池中的体积。可以看作求长是8米，宽是5米，高是1.2米的长方体的体积，因此求水的体积用长方体的体积计算公式计算，列式为：8×5×1.2.
8×5×1.2= 40×1.2=48（m³）答：池中有水48立方米。
小明说：正方体的棱长或长方体的长、宽、高扩大到原来的n倍，它的体积就扩大到原来的3n倍，对吗？如果不对，请推导出正确答案。
不对，下面以正方体为例说明。原来的体积V（原）= a3 , 扩大后的体积 V（后）= n3.a3V（后）÷V（原）=n3 即正方体或长方体的长宽高扩大到原来的n倍时，它的体积就扩大到原来的n3倍。
一块正方体钢材，棱长是40厘米，把它锻造成一块高是160厘米的长方体钢材，这个长方体钢材的底面积是多少平方厘米？
锻造前后这块钢材的体积不变，因此可以求出正方体的体积，也就是长方体钢材的体积，即40×40×40=64000（厘米3）。已知长方体的高，根据V=Sh可推导出S=V÷h，由此可以求出锻造后的长方体钢材的底面积。
40×40×40=64000（cm3）64000÷160=400（cm2）答：这个长方体钢材的底面积是400平方厘米。
掌握长方体、正方体体积的计算方法；
正确计算长方体、正方体的体积，解决一些简答的实际问题。
教学建议：师生可根据本次课的综合表现进行打分。
不满意请图三颗星，满意请图四颗星，非常满意请图五颗星。
在观察、操作探究的过程中提高动手操作能力，进一步发展空间概念。
（1）一块长方体的橡皮，长是4厘米，宽是4厘米，高是3厘米，它的体积是（ ）立方厘米。（2）掌门学校要修建一个棱长是6米的正方体的蓄水池，需要挖土（ ）立方米。（3）有4立方米的沙子，要垫在长8米、宽2.5米的沙坑里，可以垫的厚度是（ ）米。（4）一个正方体的棱长扩大2倍，它的棱长总和会随之扩大（ ）倍，表面积随之扩大（ ）倍，体积也随之扩大（ ）倍。
2.计算下列图形的体积（单位：cm）。
3.下图是一个电视机的包装箱，它的长是60米、60分米、还是60厘米？宽和高呢？箱子的体积是多少？
4.王叔叔的小货车油箱的底面积是16dm2，高是25m，这个油箱的体积是多少立方米？
5.我国著名的秦始皇陵兵马俑一号俑坑长230m，宽62m，深约是5m，一号俑的占地面积有多大？容积约是多少？
（1）48； （2）216； （3）0.2； （4）2；4；8；2. 3. 长是60厘米，宽是40厘米，高是50厘米 体积： 60×40×50= 120000立方厘米=120立方分米4. 16dm2=0.16m2 0.16×25=4（立方米）答：这个油箱的体积是4立方米。
（1）V=8×5×6=240（cm³）（2）V=5³=125（cm³）