第4章 指数函数与对数函数-综合检测3（拔尖卷）-2022-2023学年高一数学阶段性复习精选精练（人教A版2019必修第一册）

这是一份第4章 指数函数与对数函数-综合检测3（拔尖卷）-2022-2023学年高一数学阶段性复习精选精练（人教A版2019必修第一册），文件包含第4章指数函数与对数函数-综合检测3拔尖卷解析版docx、第4章指数函数与对数函数-综合检测3拔尖卷原卷版docx等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

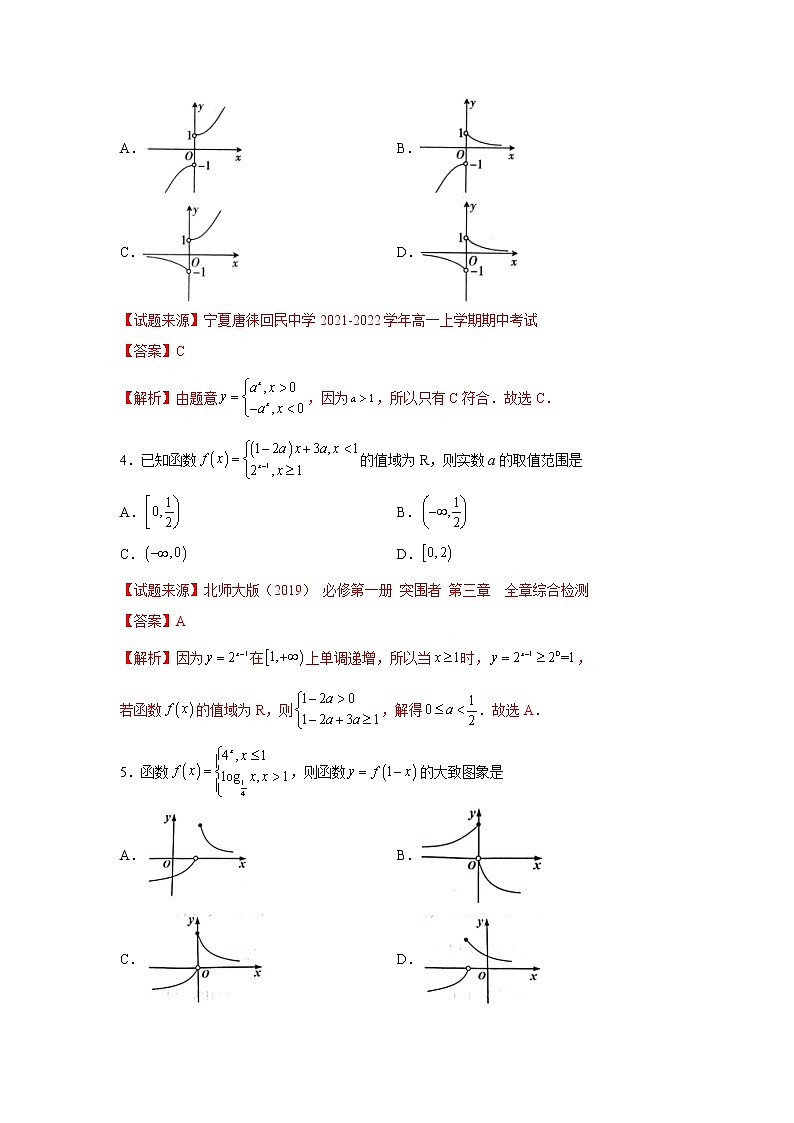
第4章 指数函数与对数函数本卷满分150分，考试时间120分钟。一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．1．下列各式正确的是A． B．C． D．【试题来源】四川省成都市双流中学2020-2021学年高一上学期期中【答案】C【解析】对于A，，故A不正确；对于B，，当时无意义，故B不正确；对于C，，故C正确；对于D，，故D不正确．故选C．2．已知函数，若，则A． B．C． D．【试题来源】山西省长治市第二中学2022届高三上学期第三次练考【答案】D【解析】因为，所以，，则，因为，所以．故选D．3．函数的大致图象是A． B．C． D．【试题来源】宁夏唐徕回民中学2021-2022学年高一上学期期中考试【答案】C【解析】由题意，因为，所以只有C符合．故选C．4．已知函数的值域为R，则实数a的取值范围是A． B．C． D．【试题来源】北师大版（2019） 必修第一册 突围者 第三章 全章综合检测【答案】A【解析】因为在上单调递增，所以当时，，若函数的值域为R，则，解得．故选A．5．函数，则函数的大致图象是A． B．C． D．【试题来源】山东省济宁邹城市2021-2022学年高三上学期期中考试【答案】C【解析】当，则，则，当，则，则，所以，所以时，递减且值域为；时，递增且值域为；只有C符合要求．故选C6．已知定义在上的函数（为实数）为偶函数，记，，，则，，的大小关系为A． B．C． D．【试题来源】山东师范大学附属中学2021-2022学年高三上学期第二次月考【答案】C【解析】（为实数）为偶函数，在上是单调增函数，，，，且，，，故选C7．已知函数的定义域为，满足对任意，恒有，若函数的零点个数为有限的个，则的最大值为A． B．C． D．【试题来源】上海市杨浦区控江中学2022届高三上学期第一次月考（9月）【答案】B【解析】令，则有，故，所以，若，则开口向上，对称轴为且，，所以在上有两个零点，即函数的零点个数最多有2个．故选B8．以下四种说法中，正确的是A．幂函数增长的速度比一次函数增长的速度快B．对任意的，C．对任意的，D．一定存在，当，，时，总有【试题来源】湘教版（2019） 必修第一册 突围者 第4章【答案】D【解析】A．如函数和，的图象如图所示：由图象知错误； B．当 时，的图象如图所示：由图象知错误；C． 当 时，的图象如图所示：由图象知错误；D． 当 时，的图象如图所示：由图象知正确；故选D．二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．9．已知，，则下列各式运算正确的是A． B．C． D．【试题来源】北师大版（2019） 必修第一册 突围者 第三章 全章综合检测【答案】ABD【解析】对于 A选项，，故正确；对于B选项，，故正确；对于C选项，，故错误；对于D正确，，故正确．故选ABD10．已知定义域为的偶函数在上单调递增，且，，则下列函数中不符合上述条件的是A． B．C． D．【试题来源】广东省清远市第一中学2021-2022学年高一上学期期中【答案】ABD【解析】对A，，故A不符合；对B，函数是定义在上的奇函数，故B不符合；对C ，在上单调递增且为偶函数，又，，故C符合；对D，幂函数在上单调递减，故D不符合．故选ABD．11．高斯是德国著名的数学家，近代数学奠基者之一，用其名字命名的高斯函数为，表示不超过x的最大整数，例如：，．已知函数，，则下列叙述中正确的是A．是偶函数 B．是奇函数C．在R上是增函数 D．的值域是【试题来源】北师大版（2019） 必修第一册 突围者 第三章 全章综合检测【答案】BCD【解析】因为，所以，所以f（x）是奇函数，A错误，B正确；因为函数，函数是增函数，所以在R上是增函数，C正确；因为，所以，所以，所以当时，，当时，，当时，，所以函数的值域为{-1，0}，D正确．综上可知，B，C，D正确．故选BCD12．已知函数，，且，则下列结论错误的是A． B．C． D．【试题来源】北师大版（2019） 必修第一册 突围者 第四章 全章综合检测【答案】AD【解析】因为、、在其定义域内都是增函数，所以、在其定义域内都是增函数．因为，，且，所以，又，，且，所以，所以，即选项A错误；因为，函数、在其定义域内均为增函数，所以，所以，即选项B正确，选项D错误；令，，则，，由于，的图象都和直线相交（如图所示），且函数和函数的图象关于直线对称，直线和直线的交点为，所以，即，即选项C正确．故选AD．三、填空题：本题共4小题，每小题5分，共20分．13．已知函数．若正数，满足，则____________．【试题来源】北京市通州区2020-2021学年高一上学期期中【答案】4【解析】因为，且、，，所以．故答案为4．14．函数的零点的个数为____________．【试题来源】沪教版（2020） 必修第一册 达标检测 第五章 5．3 函数的应用【答案】1【解析】根据题意，令，则，做出函数与的图象，由图可知与的图象只有一个交点，即方程只有一个解，故函数的零点的个数为1．故答案为1．15．已知函数，，给出下列三个结论：①函数的图象与的图象关于直线轴对称；②函数的图象与的图象关于直线对称；③函数的值域与的定义域相同；④若满足，满足，则．其中正确结论的序号是____________．【试题来源】北京市通州区2020-2021学年高一上学期期中【答案】②③④【解析】因为函数与互为反函数，所以函数的图象与的图象关于直线对称，且函数的值域与的定义域相同，所以①错误，②正确，③正确，因为满足，满足，所以为函数与图象的交点的横坐标，为函数与图象的交点的横坐标，因为函数的图象与的图象关于直线对称，所以，即，所以④正确，所以正确结论的序号是②③④，故答案为②③④．16．已知函数，若对于恒成立，则实数a的取值范围是____________．【试题来源】黑龙江省龙东地区四校2021-2022学年高三上学期联考【答案】【解析】因为 ，，所以不等式可化为，又对于恒成立，所以对于恒成立，所以，又，当且仅当时等号成立，所以，所以实数a的取值范围是．故答案为．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（10分）求下列各式中x的值：（1）；（2）；（3）；（4）．【答案】（1），（2），（3），（4）【解析】（1）因为，所以；（2）因为，所以，所以，因为且，所以；（3）因为，所以，所以；（4）因为，所以，即，所以，所以18．（12分）已知x、y、z为非零实数，且．求证：．【试题来源】沪教版（2020） 必修第一册 达标检测 期末测试【答案】证明见解析【解析】设，则，，，即，，．所以，得证．19．（12分）已知全集，集合，．（1）求p和q的值；（2）求的值．【试题来源】沪教版（2020） 必修第一册 达标检测 第三章 3．1 幂与指数【答案】（1），，（2）【解析】（1）由全集及，得，所以，．（2）．20．（12分）已知函数．（1）用定义证明在区间上单调递减；（2）求函数在区间上的最大值；（3）若，求的取值范围．【试题来源】北京市大兴区2021-2022学年高一上学期期中考试【答案】（1）证明见解析，（2），（3）【解析】（1）因为，设任意的，且，则，因为，且，所以，，所以，所以在上单调递减；（2）由（1）可知在上单调递减，所以（3）因为、，且在上单调递减，所以等价于，即，所以，所以，所以，即21．（12分）已知函数的表达式为．（1）若，，求的值域．（2）当时，求的最小值．（3）对于（2）中的函数，是否存在实数m、n，同时满足：①；②当的定义域为[m，n]时，其值域为？若存在，求出m、n的值；若不存在，请说明理由．【试题来源】沪教版（2020） 必修第一册 达标检测 期末测试【答案】（1），（2）（3）不存在满足条件的实数m、n，理由见解析【解析】（1）当时，由，得，因为，所以，．（2）令，因为，故，函数f（x）可转化为，①当时，；②当时，；③当时，．综上所述，．（3）因为，，在R上是严格减函数，所以在上的值域为，又在上的值域为，所以，即，两式相减，得，因为，所以，而由，可得，与矛盾．所以，不存在满足条件的实数m、n．22．（12分）设为奇函数，为常数．（1）求的值；（2）证明：在内单调递增；（3）若对于上的每一个的值，不等式恒成立，求实数的取值范围．【试题来源】广东省清远市第一中学2021-2022学年高一上学期期中【答案】（1），（2）证明见解析，（3）【解析】（1），，，即，故，，当时，，不成立，舍去；当时，，验证满足．综上所述：．（2），函数定义域为，考虑，设，则，，，故，函数单调递减．在上单调递减，根据复合函数单调性知在内单调递增．（3），即，为增函数．故在单调递增，故．故．