安徽省合肥蜀山区七校联考2022年中考数学押题试卷含解析

这是一份安徽省合肥蜀山区七校联考2022年中考数学押题试卷含解析，共24页。试卷主要包含了答题时请按要求用笔，有下列四个命题，如图，，则的度数为等内容，欢迎下载使用。
2021-2022中考数学模拟试卷
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（共10小题，每小题3分，共30分）
1．如图,在中， ,以边的中点为圆心,作半圆与相切，点分别是边和半圆上的动点,连接,则长的最大值与最小值的和是（ ）

A． B． C． D．
2．已知等腰三角形的两边长分别为5和6，则这个等腰三角形的周长为（　　）
A．11 B．16 C．17 D．16或17
3．如图，直线a∥b，直线c与直线a、b分别交于点A、点B，AC⊥AB于点A，交直线b于点C．如果∠1=34°，那么∠2的度数为（ ）

A．34° B．56° C．66° D．146°
4．在如图所示的数轴上，点B与点C关于点A对称，A、B两点对应的实数分别是和﹣1，则点C所对应的实数是( )

A．1+ B．2+ C．2﹣1 D．2+1
5．下列式子中，与互为有理化因式的是（　　）
A． B． C． D．
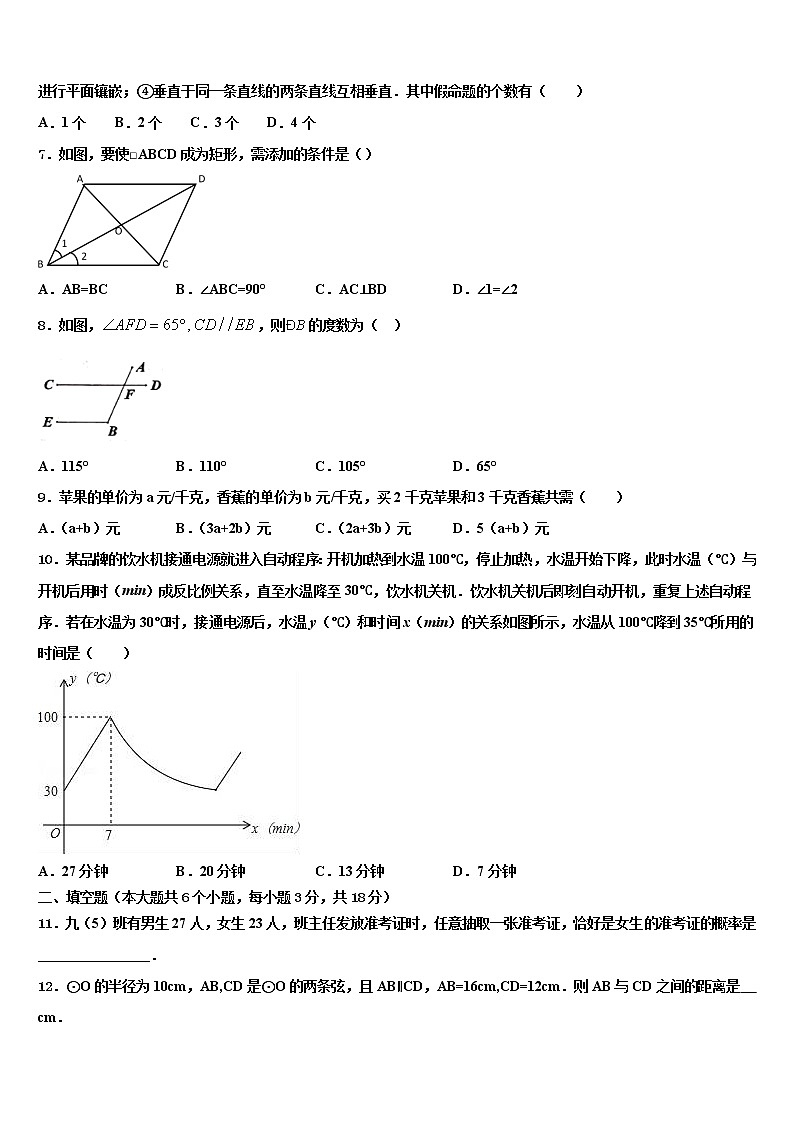
6．有下列四个命题：①相等的角是对顶角；②两条直线被第三条直线所截，同位角相等；③同一种正五边形一定能进行平面镶嵌；④垂直于同一条直线的两条直线互相垂直．其中假命题的个数有（　　）
A．1个 B．2个 C．3个 D．4个
7．如图，要使□ABCD成为矩形，需添加的条件是（）

A．AB=BC B．∠ABC=90° C．AC⊥BD D．∠1=∠2
8．如图，，则的度数为（ ）

A．115° B．110° C．105° D．65°
9．苹果的单价为a元/千克，香蕉的单价为b元/千克，买2千克苹果和3千克香蕉共需（　　）
A．（a+b）元 B．（3a+2b）元 C．（2a+3b）元 D．5（a+b）元
10．某品牌的饮水机接通电源就进入自动程序：开机加热到水温100℃，停止加热，水温开始下降，此时水温（℃）与开机后用时（min）成反比例关系，直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时，接通电源后，水温y（℃）和时间x（min）的关系如图所示，水温从100℃降到35℃所用的时间是（　　）

A．27分钟 B．20分钟 C．13分钟 D．7分钟
二、填空题（本大题共6个小题，每小题3分，共18分）
11．九（5）班有男生27人，女生23人，班主任发放准考证时，任意抽取一张准考证，恰好是女生的准考证的概率是________________．
12．⊙O的半径为10cm，AB,CD是⊙O的两条弦，且AB∥CD，AB=16cm,CD=12cm．则AB与CD之间的距离是 cm．
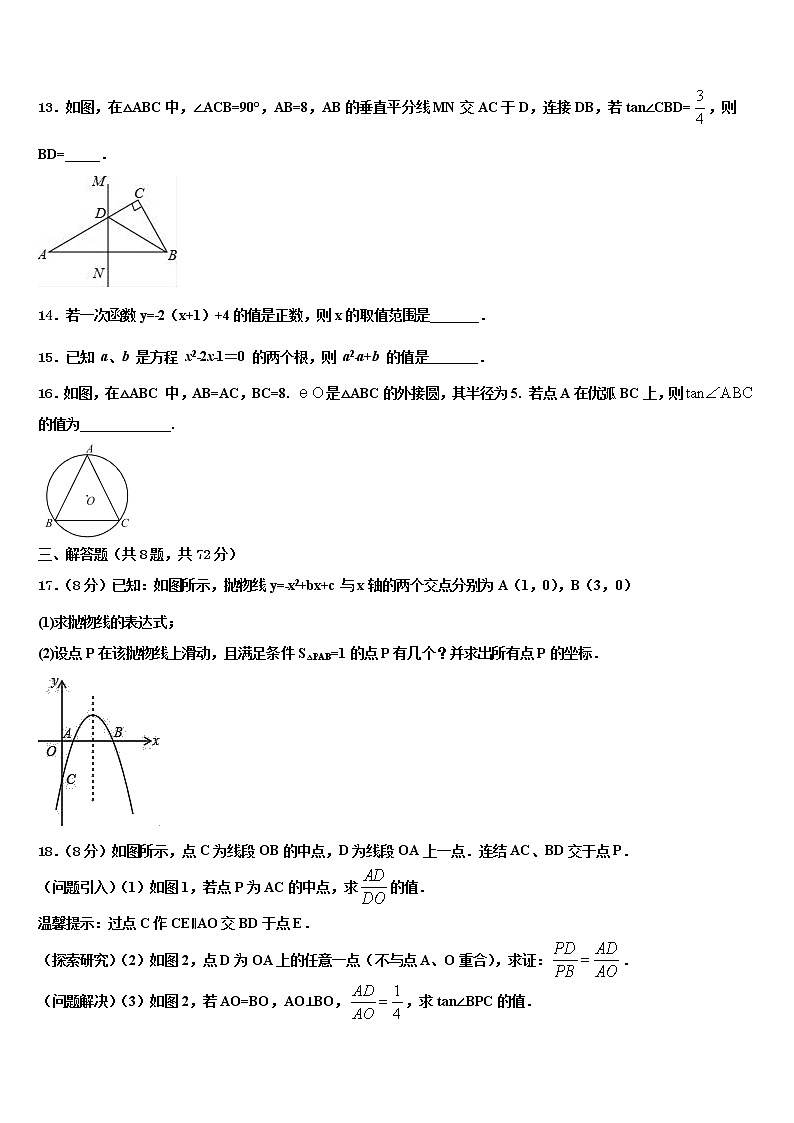
13．如图，在△ABC中，∠ACB=90°，AB=8，AB的垂直平分线MN交AC于D，连接DB，若tan∠CBD=，则BD=_____．

14．若一次函数y=﹣2（x+1）+4的值是正数，则x的取值范围是_______．
15．已知 a、b 是方程 x2﹣2x﹣1＝0 的两个根，则 a2﹣a+b 的值是_______．
16．如图，在△ABC 中，AB=AC，BC=8. 是△ABC的外接圆，其半径为5. 若点A在优弧BC上，则的值为_____________.

三、解答题（共8题，共72分）
17．（8分）已知：如图所示，抛物线y=﹣x2+bx+c与x轴的两个交点分别为A（1，0），B（3，0）
(1)求抛物线的表达式；
(2)设点P在该抛物线上滑动，且满足条件S△PAB=1的点P有几个？并求出所有点P的坐标．

18．（8分）如图所示，点C为线段OB的中点，D为线段OA上一点．连结AC、BD交于点P．
（问题引入）（1）如图1，若点P为AC的中点，求的值．
温馨提示：过点C作CE∥AO交BD于点E．
（探索研究）（2）如图2，点D为OA上的任意一点（不与点A、O重合），求证：．
（问题解决）（3）如图2，若AO=BO，AO⊥BO，，求tan∠BPC的值．

19．（8分）如图，抛物线y=ax2﹣2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A、B，点A坐标为（4，0）．
（1）求该抛物线的解析式；
（2）抛物线的顶点为N，在x轴上找一点K，使CK+KN最小，并求出点K的坐标；
（3）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CQE的面积最大时，求点Q的坐标；
（4）若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）．问：是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

20．（8分）在甲、乙两个不透明的布袋里，都装有3个大小、材质完全相同的小球，其中甲袋中的小球上分别标有数字1，1，2；乙袋中的小球上分别标有数字﹣1，﹣2，1．现从甲袋中任意摸出一个小球，记其标有的数字为x，再从乙袋中任意摸出一个小球，记其标有的数字为y，以此确定点M的坐标（x，y）．请你用画树状图或列表的方法，写出点M所有可能的坐标；求点M（x，y）在函数y=﹣的图象上的概率．
21．（8分）第二十四届冬季奧林匹克运动会将于2022年2月4日至2月20日在北京举行，北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛，甲、乙两校各有名学生参加活动，为了解这两所学校的成绩情况，进行了抽样调查，过程如下，请补充完整.
[收集数据]
从甲、乙两校各随机抽取名学生，在这次竞赛中他们的成绩如下:
甲：

乙：

[整理、描述数据]按如下分数段整理、描述这两组样本数据:
学校
人数
成绩



甲



乙



(说明:优秀成绩为，良好成绩为合格成绩为.)
[分析数据]两组样本数据的平均分、中位数、众数如下表所示:
学校
平均分
中位数
众数
甲



乙



其中 .
[得出结论]
（1）小明同学说:“这次竞赛我得了分，在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生；(填“甲”或“乙”)
（2）张老师从乙校随机抽取--名学生的竞赛成绩，试估计这名学生的竞赛成绩为优秀的概率为_ ；
（3）根据以上数据推断一所你认为竞赛成绩较好的学校，并说明理由: ；
(至少从两个不同的角度说明推断的合理性)
22．（10分）先化简，再求值：（﹣）÷，其中x的值从不等式组的整数解中选取．
23．（12分）如图，在△ABC中，BD平分∠ABC，AE⊥BD于点O，交BC于点E，AD∥BC，连接CD．
（1）求证：AO＝EO；
（2）若AE是△ABC的中线，则四边形AECD是什么特殊四边形？证明你的结论．

24．如图，二次函数y=ax2+2x+c的图象与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，3）．
（1）求该二次函数的表达式；
（2）过点A的直线AD∥BC且交抛物线于另一点D，求直线AD的函数表达式；
（3）在（2）的条件下，请解答下列问题：
①在x轴上是否存在一点P，使得以B、C、P为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，请说明理由；
②动点M以每秒1个单位的速度沿线段AD从点A向点D运动，同时，动点N以每秒个单位的速度沿线段DB从点D向点B运动，问：在运动过程中，当运动时间t为何值时，△DMN的面积最大，并求出这个最大值．




参考答案

一、选择题（共10小题，每小题3分，共30分）
1、C
【解析】
如图，设⊙O与AC相切于点E，连接OE，作OP1⊥BC垂足为P1交⊙O于Q1，此时垂线段OP1最短，P1Q1最小值为OP1-OQ1，求出OP1，如图当Q2在AB边上时，P2与B重合时，P2Q2最大值=5+3=8，由此不难解决问题．
【详解】
解：如图，设⊙O与AC相切于点E，连接OE，作OP1⊥BC垂足为P1交⊙O于Q1，

此时垂线段OP1最短，P1Q1最小值为OP1-OQ1，
∵AB=10，AC=8，BC=6，
∴AB2=AC2+BC2，
∴∠C=10°，
∵∠OP1B=10°，
∴OP1∥AC
∵AO=OB，\
∴P1C=P1B，
∴OP1=AC=4，
∴P1Q1最小值为OP1-OQ1=1，
如图，当Q2在AB边上时，P2与B重合时，P2Q2经过圆心，经过圆心的弦最长，
P2Q2最大值=5+3=8，
∴PQ长的最大值与最小值的和是1．
故选：C．
【点睛】
本题考查切线的性质、三角形中位线定理等知识，解题的关键是正确找到点PQ取得最大值、最小值时的位置，属于中考常考题型．
2、D
【解析】
试题分析：由等腰三角形的两边长分别是5和6，可以分情况讨论其边长为5，5，6或者5，6，6，均满足三角形两边之和大于第三边，两边之差小于第三边的条件，所以此等腰三角形的周长为5+5+6=16或5+6+6=17.
故选项D正确.
考点：三角形三边关系；分情况讨论的数学思想
3、B
【解析】
分析：先根据平行线的性质得出∠2+∠BAD=180°，再根据垂直的定义求出∠2的度数．
详解：∵直线a∥b，∴∠2+∠BAD=180°．
∵AC⊥AB于点A，∠1=34°，∴∠2=180°﹣90°﹣34°=56°．
故选B．

点睛：本题主要考查了平行线的性质，解题的关键是掌握两直线平行，同旁内角互补，此题难度不大．
4、D
【解析】
设点C所对应的实数是x．根据中心对称的性质，对称点到对称中心的距离相等，则有
，解得.
故选D.
5、B
【解析】
直接利用有理化因式的定义分析得出答案．
【详解】
∵（）（，）
=12﹣2，
=10，
∴与互为有理化因式的是：，
故选B．
【点睛】
本题考查了有理化因式，如果两个含有二次根式的非零代数式相乘，它们的积不含有二次根式，就说这两个非零代数式互为有理化因式. 单项二次根式的有理化因式是它本身或者本身的相反数；其他代数式的有理化因式可用平方差公式来进行分步确定.
6、D
【解析】
根据对顶角的定义，平行线的性质以及正五边形的内角及镶嵌的知识，逐一判断．
【详解】
解：①对顶角有位置及大小关系的要求，相等的角不一定是对顶角，故为假命题；
②只有当两条平行直线被第三条直线所截，同位角相等，故为假命题；
③正五边形的内角和为540°，则其内角为108°，而360°并不是108°的整数倍，不能进行平面镶嵌，故为假命题；
④在同一平面内，垂直于同一条直线的两条直线平行，故为假命题．
故选：D．
【点睛】
本题考查了命题与证明．对顶角，垂线，同位角，镶嵌的相关概念．关键是熟悉这些概念，正确判断．
7、B
【解析】
根据一个角是90度的平行四边形是矩形进行选择即可．
【详解】
解：A、是邻边相等，可判定平行四边形ABCD是菱形；
B、是一内角等于90°，可判断平行四边形ABCD成为矩形；
C、是对角线互相垂直，可判定平行四边形ABCD是菱形；
D、是对角线平分对角，可判断平行四边形ABCD成为菱形；
故选：B．
【点睛】
本题主要应用的知识点为：矩形的判定． ①对角线相等且相互平分的四边形为矩形．②一个角是90度的平行四边形是矩形．
8、A
【解析】
根据对顶角相等求出∠CFB＝65°，然后根据CD∥EB，判断出∠B＝115°．
【详解】
∵∠AFD＝65°，
∴∠CFB＝65°，
∵CD∥EB，
∴∠B＝180°−65°＝115°，
故选：A．
【点睛】
本题考查了平行线的性质，知道“两直线平行，同旁内角互补”是解题的关键．
9、C
【解析】
用单价乘数量得出买2千克苹果和3千克香蕉的总价，再进一步相加即可．
【详解】
买单价为a元的苹果2千克用去2a元，买单价为b元的香蕉3千克用去3b元，
共用去：(2a+3b)元.
故选C.
【点睛】
本题主要考查列代数式，总价=单价乘数量.
10、C
【解析】
先利用待定系数法求函数解析式，然后将y=35代入，从而求解．
【详解】
解：设反比例函数关系式为：，将（7，100）代入，得k=700，
∴，
将y=35代入，
解得；
∴水温从100℃降到35℃所用的时间是：20－7=13，
故选C．
【点睛】
本题考查反比例函数的应用，利用数形结合思想解题是关键．

二、填空题（本大题共6个小题，每小题3分，共18分）
11、
【解析】
用女生人数除以总人数即可.
【详解】
由题意得，恰好是女生的准考证的概率是.
故答案为：.
【点睛】
此题考查了概率公式，如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．
12、2或14
【解析】
分两种情况进行讨论：①弦AB和CD在圆心同侧；②弦AB和CD在圆心异侧；作出半径和弦心距，利用勾股定理和垂径定理求解即可.
【详解】
①当弦AB和CD在圆心同侧时,如图,

∵AB=16cm，CD=12cm，
∴AE=8cm，CF=6cm，
∵OA=OC=10cm，
∴EO=6cm，OF=8cm，
∴EF=OF−OE=2cm；
②当弦AB和CD在圆心异侧时,如图,

∵AB=16cm，CD=12cm，
∴AF=8cm，CE=6cm，
∵OA=OC=10cm，
∴OF=6cm，OE=8cm，
∴EF=OF+OE=14cm.
∴AB与CD之间的距离为14cm或2cm.
故答案为：2或14.
13、2．
【解析】
由tan∠CBD== 设CD=3a、BC=4a，据此得出BD=AD=5a、AC=AD+CD=8a，由勾股定理可得（8a）2+（4a）2=82，解之求得a的值可得答案．
【详解】
解：在Rt△BCD中，∵tan∠CBD==，
∴设CD=3a、BC=4a，
则BD=AD=5a，
∴AC=AD+CD=5a+3a=8a，
在Rt△ABC中，由勾股定理可得（8a）2+（4a）2=82，
解得：a= 或a=-（舍），
则BD=5a=2，
故答案为2．
【点睛】
本题考查线段垂直平分线上的点到线段两端点的距离相等的性质，勾股定理的应用，解题关键是熟记性质与定理并准确识图．
14、x＜1
【解析】
根据一次函数的性质得出不等式解答即可．
【详解】
因为一次函数y=﹣2（x+1）+4的值是正数，
可得：﹣2（x+1）+4＞0，
解得：x＜1，
故答案为x＜1.
【点睛】
本题考查了一次函数与一元一次不等式，根据题意正确列出不等式是解题的关键.
15、1
【解析】
根据一元二次方程的解及根与系数的关系，可得出a2-2a=1、a+b=2，将其代入a2-a+b中即可求出结论．
【详解】
∵a、b是方程x2-2x-1=0的两个根，
∴a2-2a=1，a+b=2，
∴a2-a+b=a2-2a+（a+b）=1+2=1．
故答案为1．
【点睛】
本题考查根与系数的关系以及一元二次方程的解，牢记两根之和等于-、两根之积等于是解题的关键．
16、2
【解析】
【分析】作高线AD，由等腰三角形的性质可知D为BC的中点，即AD为BC的垂直平分线，根据垂径定理，AD过圆心O，由BC的长可得出BD的长，根据勾股定理求出半径，继而可得AD的长，在直角三角形ABD中根据正切的定义求解即可.
试题解析：如图，作AD⊥BC，垂足为D，连接OB，
∵AB=AC，∴BD=CD=BC=×8=4，
∴AD垂直平分BC，
∴AD过圆心O，
在Rt△OBD中，OD==3，
∴AD=AO+OD=8，
在Rt△ABD中，tan∠ABC==2，
故答案为2.

【点睛】本题考查了垂径定理、等腰三角形的性质、正切的定义等知识，综合性较强，正确添加辅助线构造直角三角形进行解题是关键.

三、解答题（共8题，共72分）
17、 (1)y=﹣x2+4x﹣3；(2)满足条件的P点坐标有3个，它们是（2，1）或（2+，﹣1）或（2﹣，﹣1）．
【解析】
（1）由于已知抛物线与x轴的交点坐标，则可利用交点式求出抛物线解析式；
（2）根据二次函数图象上点的坐标特征，可设P（t，-t2+4t-3），根据三角形面积公式得到 •2•|-t2+4t-3|=1，然后去绝对值得到两个一元二次方程，再解方程求出t即可得到P点坐标.
【详解】
解:(1)抛物线解析式为y=﹣（x﹣1）（x﹣3）=﹣x2+4x﹣3；
(2)设P（t，﹣t2+4t﹣3），
因为S△PAB=1，AB=3﹣1=2，
所以•2•|﹣t2+4t﹣3|=1，
当﹣t2+4t﹣3=1时，t1=t2=2，此时P点坐标为（2，1）；
当﹣t2+4t﹣3=﹣1时，t1=2+，t2=2﹣，此时P点坐标为（2+，﹣1）或（2﹣，﹣1），
所以满足条件的P点坐标有3个，它们是（2，1）或（2+，﹣1）或（2﹣，﹣1）．
【点睛】
本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解.
18、（1）；(2) 见解析；(3)
【解析】
（1）过点C作CE∥OA交BD于点E，即可得△BCE∽△BOD，根据相似三角形的性质可得，再证明△ECP≌△DAP，由此即可求得的值；（2）过点D作DF∥BO交AC于点F，即可得，，由点C为OB的中点可得BC=OC，即可证得；（3）由（2）可知=，设AD=t，则BO=AO=4t，OD=3t，根据勾股定理求得BD=5t，即可得PD=t，PB=4t，所以PD=AD，从而得∠A=∠APD=∠BPC，所以tan∠BPC=tan∠A=．
【详解】
（1）如图1，过点C作CE∥OA交BD于点E，

∴△BCE∽△BOD，
∴=，
又BC=BO，∴CE=DO．
∵CE∥OA，∴∠ECP=∠DAP，
又∠EPC=∠DPA，PA=PC，
∴△ECP≌△DAP，
∴AD=CE=DO，
即 =；
（2）如图2，过点D作DF∥BO交AC于点F，

则 =， =．
∵点C为OB的中点，
∴BC=OC，
∴=；
（3）如图2，∵=，
由（2）可知==．
设AD=t，则BO=AO=4t，OD=3t，
∵AO⊥BO，即∠AOB=90°，
∴BD==5t，
∴PD=t，PB=4t，
∴PD=AD，
∴∠A=∠APD=∠BPC，
则tan∠BPC=tan∠A==．
【点睛】
本题考查了相似三角形的判定与性质，准确作出辅助线，构造相似三角形是解决本题的关键，也是求解的难点．
19、（1）y=﹣；（1）点K的坐标为（，0）；（2）点P的坐标为：（1+，1）或（1﹣，1）或（1+，2）或（1﹣，2）．
【解析】
试题分析：（1）把A、C两点坐标代入抛物线解析式可求得a、c的值，可求得抛物线解析；
（1）可求得点C关于x轴的对称点C′的坐标，连接C′N交x轴于点K，再求得直线C′K的解析式，可求得K点坐标；
（2）过点E作EG⊥x轴于点G，设Q（m，0），可表示出AB、BQ，再证明△BQE≌△BAC，可表示出EG，可得出△CQE关于m的解析式，再根据二次函数的性质可求得Q点的坐标；
（4）分DO=DF、FO=FD和OD=OF三种情况，分别根据等腰三角形的性质求得F点的坐标，进一步求得P点坐标即可．
试题解析：（1）∵抛物线经过点C（0，4），A（4，0），
∴，解得 ，
∴抛物线解析式为y=﹣ x1+x+4；
（1）由（1）可求得抛物线顶点为N（1， ），
如图1，作点C关于x轴的对称点C′（0，﹣4），连接C′N交x轴于点K，则K点即为所求，

设直线C′N的解析式为y=kx+b，把C′、N点坐标代入可得 ，解得 ，
∴直线C′N的解析式为y=x-4 ，
令y=0，解得x= ，
∴点K的坐标为（，0）；
（2）设点Q（m，0），过点E作EG⊥x轴于点G，如图1，

由﹣ x1+x+4=0，得x1=﹣1，x1=4，
∴点B的坐标为（﹣1，0），AB=6，BQ=m+1，
又∵QE∥AC，∴△BQE≌△BAC，
∴ ，即 ，解得EG= ；
∴S△CQE=S△CBQ﹣S△EBQ=（CO-EG）·BQ=（m+1）（4-）
= =-（m-1）1+2 ．
又∵﹣1≤m≤4，
∴当m=1时，S△CQE有最大值2，此时Q（1，0）；
（4）存在．在△ODF中，
（ⅰ）若DO=DF，∵A（4，0），D（1，0），
∴AD=OD=DF=1．
又在Rt△AOC中，OA=OC=4，
∴∠OAC=45°．
∴∠DFA=∠OAC=45°．
∴∠ADF=90°．
此时，点F的坐标为（1，1）．
由﹣ x1+x+4=1，得x1=1+ ，x1=1﹣．
此时，点P的坐标为：P1（1+，1）或P1（1﹣，1）；
（ⅱ）若FO=FD，过点F作FM⊥x轴于点M．

由等腰三角形的性质得：OM=OD=1，
∴AM=2．
∴在等腰直角△AMF中，MF=AM=2．
∴F（1，2）．
由﹣ x1+x+4=2，得x1=1+，x1=1﹣．
此时，点P的坐标为：P2（1+，2）或P4（1﹣，2）；
（ⅲ）若OD=OF，
∵OA=OC=4，且∠AOC=90°．
∴AC=4．
∴点O到AC的距离为1．
而OF=OD=1＜1，与OF≥1矛盾．
∴在AC上不存在点使得OF=OD=1．
此时，不存在这样的直线l，使得△ODF是等腰三角形．
综上所述，存在这样的直线l，使得△ODF是等腰三角形．所求点P的坐标为：（1+，1）或（1﹣，1）或（1+，2）或（1﹣，2）．
点睛：本题是二次函数综合题，主要考查待定系数法、三角形全等的判定与性质、等腰三角形的性质等，能正确地利用数形结合思想、分类讨论思想等进行解题是关键.
20、（1）树状图见解析，则点M所有可能的坐标为：（1，﹣1），（1，﹣2），（1，1），（1，﹣1），（1，﹣2），（1，1），（2，﹣1），（2，﹣2），（2，1）；（2）.
【解析】
试题分析：（1）画出树状图，可求得所有等可能的结果；（2）由点M（x，y）在函数y=﹣的图象上的有：（1，﹣2），（2，﹣1），直接利用概率公式求解即可求得答案．
试题解析：（1）树状图如下图：

则点M所有可能的坐标为：（1，﹣1），（1，﹣2），（1，1），（1，﹣1），（1，﹣2），（1，1），（2，﹣1），（2，﹣2），（2，1）；（2）∵点M（x，y）在函数y=﹣的图象上的有：（1，﹣2），（2，﹣1），
∴点M（x，y）在函数y=﹣的图象上的概率为：．
考点：列表法或树状图法求概率.
21、80；（1）甲；（2）；（3）乙学校竞赛成绩较好，理由见解析
【解析】
首先根据乙校的成绩结合众数的定义即可得出a的值；
（1）根据两个学校成绩的中位数进一步判断即可；
（2）根据概率的定义，结合乙校优秀成绩的概率进一步求解即可；
（3）根据题意，从平均数以及中位数两方面加以比较分析即可.
【详解】
由乙校成绩可知，其中80出现的次数最多，故80为该组数据的众数，∴a=80，
故答案为：80；
（1）由表格可知，甲校成绩的中位数为60，乙校成绩的中位数为75，
∵小明这次竞赛得了分，在他们学校排名属中游略偏上，
∴小明为甲校学生，
故答案为：甲；
（2）乙校随便抽取一名学生的成绩，该学生成绩为优秀的概率为：，
故答案为：；
（3）乙校竞赛成绩较好，理由如下：
因为乙校的平均分高于甲校的平均分说明平均水平高，乙校的中位数75高于甲校的中位数65，说明乙校分数不低于70分的学生比甲校多，综上所述，乙校竞赛成绩较好.
【点睛】
本题主要考查了众数、中位数、平均数的定义与简单概率的计算的综合运用，熟练掌握相关概念是解题关键.
22、-
【解析】
先化简，再解不等式组确定x的值，最后代入求值即可.
【详解】
（﹣）÷，
=÷
=
解不等式组，
可得：﹣2＜x≤2，
∴x=﹣1，0，1，2，
∵x=﹣1，0，1时，分式无意义，
∴x=2，
∴原式==﹣．
23、（1）详见解析；（2）平行四边形.
【解析】
（1）由“三线合一”定理即可得到结论；
（2）由AD∥BC，BD平分∠ABC，得到∠ADB=∠ABD，由等腰三角形的判定得到AD=AB，根据垂直平分线的性质有AB=BE，于是AD=BE，进而得到AD=EC，根据平行四边形的判定即可得到结论．
【详解】
证明：（1）∵BD平分∠ABC，AE⊥BD，
∴AO=EO；
（2）平行四边形，
证明：∵AD∥BC，
∴∠ADB=∠ABD，
∴AD=AB，
∵OA=OE，OB⊥AE，
∴AB=BE，
∴AD=BE，
∵BE=CE，
∴AD=EC，
∴四边形AECD是平行四边形．

【点睛】
考查等腰直角三角形的性质以及平行四边形的判定，掌握平行四边形的判定方法是解题的关键.
24、（1）y=﹣x2+2x+3；（2）y=﹣x﹣1；（3）P（）或P（﹣4.5，0）；当t=时，S△MDN的最大值为．
【解析】
（1）把A（-1，0），C（0，3）代入y=ax2+2x+c即可得到结果；
（2）在y=-x2+2x+3中，令y=0，则-x2+2x+3=0，得到B（3，0），由已知条件得直线BC的解析式为y=-x+3，由于AD∥BC，设直线AD的解析式为y=-x+b，即可得到结论；
（3）①由BC∥AD，得到∠DAB=∠CBA，全等只要当或时，△PBC∽△ABD，解方程组得D(4,−5)，求得
设P的坐标为（x，0），代入比例式解得或x=−4.5,即可得到或P(−4.5,0)；
②过点B作BF⊥AD于F，过点N作NE⊥AD于E，在Rt△AFB中，∠BAF=45°，于是得到sin∠BAF 求得求得 由于于是得到即可得到结果．
【详解】
(1)由题意知：
解得
∴二次函数的表达式为
(2)在 中,令y=0,则
解得：
∴B(3,0)，
由已知条件得直线BC的解析式为y=−x+3，
∵AD∥BC，
∴设直线AD的解析式为y=−x+b，
∴0=1+b，
∴b=−1，
∴直线AD的解析式为y=−x−1；
(3)①∵BC∥AD，
∴∠DAB=∠CBA，
∴只要当：或时,△PBC∽△ABD，
解得D(4,−5)，
∴
设P的坐标为(x,0)，
即或
解得或x=−4.5,
∴或P(−4.5,0)，
②过点B作BF⊥AD于F，过点N作NE⊥AD于E，

在Rt△AFB中,
∴sin∠BAF
∴
∴
∵
又∵
∴




∴当时,的最大值为
【点睛】
属于二次函数的综合题，考查待定系数法求二次函数解析式，锐角三角形函数，相似三角形的判定与性质，二次函数的最值等，综合性比较强，难度较大.