安徽省合肥市北城片区市级名校2022年中考数学全真模拟试题含解析

这是一份安徽省合肥市北城片区市级名校2022年中考数学全真模拟试题含解析，共20页。试卷主要包含了考生必须保证答题卡的整洁，如图，一段抛物线等内容，欢迎下载使用。
2021-2022中考数学模拟试卷
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题（共10小题，每小题3分，共30分）
1．如图，将边长为3a的正方形沿虚线剪成两块正方形和两块长方形．若拿掉边长2b的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为（　　）

A．3a+2b B．3a+4b C．6a+2b D．6a+4b
2．如图，以正方形ABCD的边CD为边向正方形ABCD外作等边△CDE，AC与BE交于点F，则∠AFE的度数是（　　）

A．135° B．120° C．60° D．45°
3．下列二次函数的图象，不能通过函数y=3x2的图象平移得到的是（   ）
A．y=3x2+2 B．y=3（x﹣1）2 C．y=3（x﹣1）2+2 D．y=2x2
4．△ABC的三条边长分别是5，13，12，则其外接圆半径和内切圆半径分别是（　　）
A．13，5 B．6.5，3 C．5，2 D．6.5，2
5．如图，是一次函数y=kx+b与反比例函数y=的图象，则关于x的不等式kx+b＞的解集为

A．x＞1 B．﹣2＜x＜1
C．﹣2＜x＜0或x＞1 D．x＜﹣2
6．计算1+2+22+23+…+22010的结果是( )
A．22011–1 B．22011+1
C． D．
7．如图，一段抛物线：y=﹣x（x﹣5）（0≤x≤5），记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2， 交x轴于点A2；将C2绕点A2旋转180°得C3， 交x轴于点A3；…如此进行下去，得到一“波浪线”，若点P（2018，m）在此“波浪线”上，则m的值为（   ）

A．4 B．﹣4 C．﹣6 D．6
8．学完分式运算后，老师出了一道题“计算：”.
小明的做法：原式；
小亮的做法：原式；
小芳的做法：原式．
其中正确的是（ ）
A．小明 B．小亮 C．小芳 D．没有正确的
9．已知点，与点关于轴对称的点的坐标是（ ）
A． B． C． D．
10．小军旅行箱的密码是一个六位数，由于他忘记了密码的末位数字，则小军能一次打开该旅行箱的概率是（　　）
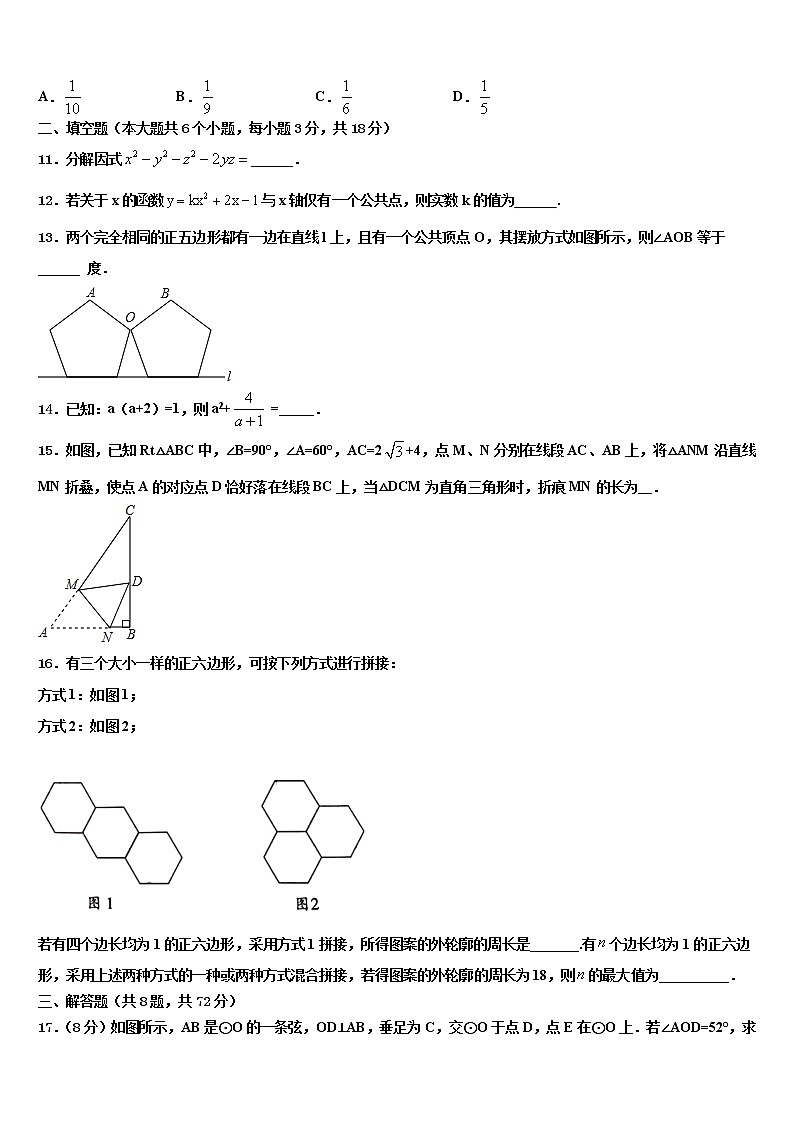
A． B． C． D．
二、填空题（本大题共6个小题，每小题3分，共18分）
11．分解因式______．
12．若关于x的函数与x轴仅有一个公共点，则实数k的值为 .
13．两个完全相同的正五边形都有一边在直线l上，且有一个公共顶点O，其摆放方式如图所示，则∠AOB等于 ______ 度．

14．已知：a（a+2）=1，则a2+ =_____．
15．如图，已知Rt△ABC中，∠B=90°，∠A=60°，AC=2+4，点M、N分别在线段AC、AB上，将△ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△DCM为直角三角形时，折痕MN的长为__．

16．有三个大小一样的正六边形，可按下列方式进行拼接：
方式1：如图1；
方式2：如图2；

若有四个边长均为1的正六边形，采用方式1拼接，所得图案的外轮廓的周长是_______.有个边长均为1的正六边形，采用上述两种方式的一种或两种方式混合拼接，若得图案的外轮廓的周长为18，则的最大值为__________．
三、解答题（共8题，共72分）
17．（8分）如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．若∠AOD=52°，求∠DEB的度数；若OC=3，OA=5，求AB的长．

18．（8分）计算：
（1）﹣12018+|﹣2|+2cos30°；
（2）（a+1）2+（1﹣a）（a+1）；
19．（8分）如图，某校数学兴趣小组要测量大楼AB的高度，他们在点C处测得楼顶B的仰角为32°，再往大楼AB方向前进至点D处测得楼顶B的仰角为48°，CD＝96m，其中点A、D、C在同一直线上．求AD的长和大楼AB的高度（结果精确到2m）参考数据：sin48°≈2．74，cos48°≈2．67，tan48°≈2．22，≈2．73

20．（8分）我市某学校在“行读石鼓阁”研学活动中，参观了我市中华石鼓园，石鼓阁是宝鸡城市新地标．建筑面积7200平方米，为我国西北第一高阁．秦汉高台门阙的建筑风格，追求稳定之中的飞扬灵动，深厚之中的巧妙组合，使景观功能和标志功能融为一体．小亮想知道石鼓阁的高是多少，他和同学李梅对石鼓阁进行测量．测量方案如下：如图，李梅在小亮和“石鼓阁”之间的直线BM上平放一平面镜，在镜面上做了一个标记，这个标记在直线BM上的对应位置为点C，镜子不动，李梅看着镜面上的标记，她来回走动，走到点D时，看到“石鼓阁”顶端点A在镜面中的像与镜面上的标记重合，这时，测得李梅眼睛与地面的高度ED=1.6米，CD=2.2米，然后，在阳光下，小亮从D点沿DM方向走了29.4米，此时“石鼓阁”影子与小亮的影子顶端恰好重合，测得小亮身高1.7米，影长FH=3.4米．已知AB⊥BM，ED⊥BM，GF⊥BM，其中，测量时所使用的平面镜的厚度忽略不计，请你根据题中提供的相关信息，求出“石鼓阁”的高AB的长度．

21．（8分）已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D．
（I）如图①，若BC为⊙O的直径，求BD、CD的长；
（II）如图②，若∠CAB=60°，求BD、BC的长．

22．（10分）在等腰Rt△ABC中，∠ACB=90°，AC=BC，点D是边BC上任意一点，连接AD，过点C作CE⊥AD于点E．
（1）如图1，若∠BAD=15°，且CE=1，求线段BD的长；
（2）如图2，过点C作CF⊥CE，且CF=CE，连接FE并延长交AB于点M，连接BF，求证：AM=BM．

23．（12分）“十九大”报告提出了我国将加大治理环境污染的力度，还我青山绿水，其中雾霾天气让环保和健康问题成为焦点，为了调查学生对雾霾天气知识的了解程度，某校在全校学生中抽取400名同学做了一次调查，根据调查统计结果，绘制了不完整的一种统计图表．

对雾霾了解程度的统计表
对雾霾的了解程度
百分比
A．非常了解
5%
B．比较了解
m
C．基本了解
45%
D．不了解
n
请结合统计图表，回答下列问题：统计表中：m＝　 　，n＝　 　；请在图1中补全条形统计图；请问在图2所示的扇形统计图中，D部分扇形所对应的圆心角是多少度？
24．如图，⊙O直径AB和弦CD相交于点E，AE＝2，EB＝6，∠DEB＝30°，求弦CD长．




参考答案

一、选择题（共10小题，每小题3分，共30分）
1、A
【解析】
根据这块矩形较长的边长＝边长为3a的正方形的边长－边长为2b的小正方形的边长＋边长为2b的小正方形的边长的2倍代入数据即可.
【详解】
依题意有：3a﹣2b+2b×2=3a﹣2b+4b=3a+2b．
故这块矩形较长的边长为3a+2b．故选A．
【点睛】
本题主要考查矩形、正方形和整式的运算，熟读题目，理解题意，清楚题中的等量关系是解答本题的关键.
2、B
【解析】
易得△ABF与△ADF全等，∠AFD=∠AFB，因此只要求出∠AFB的度数即可．
【详解】
∵四边形ABCD是正方形，
∴AB=AD，∠BAF=∠DAF，
∴△ABF≌△ADF，
∴∠AFD=∠AFB，
∵CB=CE，
∴∠CBE=∠CEB，
∵∠BCE=∠BCD+∠DCE=90°+60°=150°，
∴∠CBE=15°，
∵∠ACB=45°，
∴∠AFB=∠ACB+∠CBE=60°．
∴∠AFE=120°．
故选B．
【点睛】
此题考查正方形的性质，熟练掌握正方形及等边三角形的性质，会运用其性质进行一些简单的转化．
3、D
【解析】
分析：根据平移变换只改变图形的位置不改变图形的形状与大小对各选项分析判断后利用排除法求解：
A、y=3x2的图象向上平移2个单位得到y=3x2+2，故本选项错误；
B、y=3x2的图象向右平移1个单位得到y=3（x﹣1）2，故本选项错误；
C、y=3x2的图象向右平移1个单位，向上平移2个单位得到y=3（x﹣1）2+2，故本选项错误；
D、y=3x2的图象平移不能得到y=2x2，故本选项正确．
故选D．
4、D
【解析】
根据边长确定三角形为直角三角形,斜边即为外切圆直径,内切圆半径为,
【详解】
解：如下图,
∵△ABC的三条边长分别是5，13，12，且52+122=132,
∴△ABC是直角三角形,
其斜边为外切圆直径,
∴外切圆半径==6.5,
内切圆半径==2,
故选D.

【点睛】
本题考查了直角三角形内切圆和外切圆的半径,属于简单题,熟悉概念是解题关键.
5、C
【解析】
根据反比例函数与一次函数在同一坐标系内的图象可直接解答．
【详解】
观察图象，两函数图象的交点坐标为（1，2），（-2，-1），kx+b＞的解就是一次函数y=kx+b图象在反比例函数y=的图象的上方的时候x的取值范围，
由图象可得：-2＜x＜0或x＞1，
故选C．
【点睛】
本题考查的是反比例涵数与一次函数图象在同一坐标系中二者的图象之间的关系．一般这种类型的题不要计算反比计算表达式，解不等式，直接从从图象上直接解答．
6、A
【解析】
可设其和为S，则2S=2+22+23+24+…+22010+22011，两式相减可得答案.
【详解】
设S=1+2+22+23+…+22010①
则2S=2+22+23+…+22010+22011②
②-①得S=22011-1．
故选A.
【点睛】
本题考查了因式分解的应用；设出和为S，并求出2S进行做差求解是解题关键．
7、C
【解析】
分析：根据图象的旋转变化规律以及二次函数的平移规律得出平移后解析式，进而求出m的值，由2017÷5=403…2，可知点P（2018，m）在此“波浪线”上C404段上，求出C404的解析式，然后把P（2018，m）代入即可．
详解：当y=0时，﹣x（x﹣5）=0，解得x1=0，x2=5，则A1（5，0），
∴OA1=5，
∵将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…；如此进行下去，得到一“波浪线”，
∴A1A2=A2A3=…=OA1=5，
∴抛物线C404的解析式为y=（x﹣5×403）（x﹣5×404），即y=（x﹣2015）（x﹣2020），
当x=2018时，y=（2018﹣2015）（2018﹣2020）=﹣1，
即m=﹣1．
故选C．
点睛：此题主要考查了二次函数的平移规律，根据已知得出二次函数旋转后解析式是解题关键．
8、C
【解析】
试题解析：
=
=
=
=
=1．
所以正确的应是小芳．
故选C．
9、C
【解析】
根据关于y轴对称的点，纵坐标相同，横坐标互为相反数，可得答案．
【详解】
解：点，与点关于轴对称的点的坐标是，
故选：C．
【点睛】
本题考查了关于y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于x轴对称的点，横坐标相同，纵坐标互为相反数；关于y轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数．
10、A
【解析】
∵密码的末位数字共有10种可能（0、1、 2、 3、4、 5、 6、 7、 8、 9、 0都有可能），
∴当他忘记了末位数字时，要一次能打开的概率是.
故选A.

二、填空题（本大题共6个小题，每小题3分，共18分）
11、（x+y+z）（x﹣y﹣z）．
【解析】
当被分解的式子是四项时，应考虑运用分组分解法进行分解．本题后三项可以为一组组成完全平方式，再用平方差公式即可．
【详解】
x2-y2-z2-2yz，
=x2-（y2+z2+2yz），
=x2-（y+z）2，
=（x+y+z）（x-y-z）．
故答案为（x+y+z）（x-y-z）．
【点睛】
本题考查了用分组分解法进行因式分解．难点是采用两两分组还是三一分组．本题后三项可组成完全平方公式，可把后三项分为一组．
12、0或－1。
【解析】由于没有交待是二次函数，故应分两种情况：
当k=0时，函数是一次函数，与x轴仅有一个公共点。
当k≠0时，函数是二次函数，若函数与x轴仅有一个公共点，则有两个相等的实数根，即。
综上所述，若关于x的函数与x轴仅有一个公共点，则实数k的值为0或－1。
13、108°
【解析】
如图，易得△OCD为等腰三角形，根据正五边形内角度数可求出∠OCD，然后求出顶角∠COD，再用360°减去∠AOC、∠BOD、∠COD即可

【详解】
∵五边形是正五边形，
∴每一个内角都是108°，
∴∠OCD=∠ODC=180°-108°=72°，
∴∠COD=36°，
∴∠AOB=360°-108°-108°-36°=108°.
故答案为108°
【点睛】
本题考查正多边形的内角计算，分析出△OCD是等腰三角形，然后求出顶角是关键.
14、3
【解析】
先根据a（a+2）=1得出a2=1-2a,再把a2=1-2a代入a2+进行计算.
【详解】
a（a+2）=1得出a2=1-2a,
a2+1-2a+= ===3.
【点睛】
本题考查的是代数式求解，熟练掌握代入法是解题的关键.
15、或
【解析】
分析：依据△DCM为直角三角形，需要分两种情况进行讨论：当∠CDM=90°时，△CDM是直角三角形；当∠CMD=90°时，△CDM是直角三角形，分别依据含30°角的直角三角形的性质以及等腰直角三角形的性质，即可得到折痕MN的长．
详解：分两种情况：
①如图，当∠CDM=90°时，△CDM是直角三角形，

∵在Rt△ABC中，∠B=90°，∠A=60°，AC=2+4，
∴∠C=30°，AB=AC=+2，
由折叠可得，∠MDN=∠A=60°，
∴∠BDN=30°，
∴BN=DN=AN，
∴BN=AB=，
∴AN=2BN=，
∵∠DNB=60°，
∴∠ANM=∠DNM=60°，
∴∠AMN=60°，
∴AN=MN=；
②如图，当∠CMD=90°时，△CDM是直角三角形，

由题可得，∠CDM=60°，∠A=∠MDN=60°，
∴∠BDN=60°，∠BND=30°，
∴BD=DN=AN，BN=BD，
又∵AB=+2，
∴AN=2，BN=，
过N作NH⊥AM于H，则∠ANH=30°，
∴AH=AN=1，HN=，
由折叠可得，∠AMN=∠DMN=45°，
∴△MNH是等腰直角三角形，
∴HM=HN=，
∴MN=，
故答案为：或．
点睛：本题考查了翻折变换-折叠问题，等腰直角三角形的性质，正确的作出图形是解题的关键．折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
16、18 1
【解析】
有四个边长均为1的正六边形，采用方式1拼接，利用4n+2的规律计算；把六个正六边形围着一个正六边按照方式2进行拼接可使周长为8，六边形的个数最多．
【详解】
解：有四个边长均为1的正六边形，采用方式1拼接，所得图案的外轮廓的周长为4×4+2=18；
按下图拼接，图案的外轮廓的周长为18，此时正六边形的个数最多，即n的最大值为1．

故答案为：18；1．
【点睛】
本题考查了正多边形和圆，以及图形的变化类规律总结问题，根据题意，得出规律是解决此题的关键．

三、解答题（共8题，共72分）
17、 (1)26°;(2)1.
【解析】
试题分析：（1）根据垂径定理，得到，再根据圆周角与圆心角的关系，得知∠E=∠O，据此即可求出∠DEB的度数；
（2）由垂径定理可知，AB=2AC，在Rt△AOC中，OC=3，OA=5，由勾股定理求AC即可得到AB的长．
试题解析：（1）∵AB是⊙O的一条弦，OD⊥AB，
∴，
∴∠DEB=∠AOD=×52°=26°；
（2）∵AB是⊙O的一条弦，OD⊥AB，
∴AC=BC，即AB=2AC，
在Rt△AOC中，AC===4，
则AB=2AC=1．
考点：垂径定理；勾股定理；圆周角定理．
18、 (1)1;(2)2a+2
【解析】
（1）根据特殊角锐角三角函数值、绝对值的性质即可求出答案;
（2）先化简原式，然后将x的值代入原式即可求出答案．
【详解】
解:（1）原式=﹣1+2﹣+2×=1;
（2）原式=a2+2a+1+1﹣a2=2a+2.
【点睛】
本题考查学生的运算能力，解题的关键是熟练运用运算法则，本题属于基础题型．
19、AD的长约为225m，大楼AB的高约为226m
【解析】
首先设大楼AB的高度为xm，在Rt△ABC中利用正切函数的定义可求得 ，然后根据∠ADB的正切表示出AD的长，又由CD=96m，可得方程 ，解此方程即可求得答案．
【详解】
解：设大楼AB的高度为xm，
在Rt△ABC中，∵∠C=32°，∠BAC=92°，
∴ ，
在Rt△ABD中， ，
∴，
∵CD=AC-AD，CD=96m，
∴ ，
解得：x≈226，
∴
答：大楼AB的高度约为226m，AD的长约为225m．
【点睛】
本题考查解直角三角形的应用．要求学生能借助仰角构造直角三角形并解直角三角形，注意数形结合思想与方程思想的应用．
20、 “石鼓阁”的高AB的长度为56m．
【解析】
根据题意得∠ABC=∠EDC=90°，∠ABM=∠GFH=90°，再根据反射定律可知：∠ACB=∠ECD，则△ABC∽△EDC，根据相似三角形的性质可得=，再根据∠AHB=∠GHF，可证△ABH∽△GFH，同理得=，代入数值计算即可得出结论.
【详解】
由题意可得：∠ABC=∠EDC=90°，∠ABM=∠GFH=90°，
由反射定律可知：∠ACB=∠ECD，
则△ABC∽△EDC，
∴=，
即=①，
∵∠AHB=∠GHF，
∴△ABH∽△GFH，
∴=，即=②，
联立①②，解得：AB=56，
答：“石鼓阁”的高AB的长度为56m．
【点睛】
本题考查了相似三角形的判定与性质，解题的关键是熟练的掌握相似三角形的判定与性质.
21、（1）BD=CD=5;（2）BD=5，BC=5．
【解析】
（1）利用圆周角定理可以判定△DCB是等腰直角三角形，利用勾股定理即可解决问题；
（2）如图②，连接OB，OD．由圆周角定理、角平分线的性质以及等边三角形的判定推知△OBD是等边三角形，则BD=OB=OD=5，再根据垂径定理求出BE即可解决问题.
【详解】
（1）∵BC是⊙O的直径，
∴∠CAB=∠BDC=90°．
∵AD平分∠CAB，
∴，
∴CD=BD．
在直角△BDC中，BC=10，CD2+BD2=BC2，
∴BD=CD=5，
（2）如图②，连接OB，OD，OC，

∵AD平分∠CAB，且∠CAB=60°，
∴∠DAB=∠CAB=30°，
∴∠DOB=2∠DAB=60°．
又∵OB=OD，
∴△OBD是等边三角形，
∴BD=OB=OD．
∵⊙O的直径为10，则OB=5，
∴BD=5，
∵AD平分∠CAB，
∴，
∴OD⊥BC，设垂足为E，
∴BE=EC=OB•sin60°=，
∴BC=5．
【点睛】
本题考查圆周角定理，垂径定理，解直角三角形等知识，解题的关键是学会添加常用辅助线，属于中考常考题型．
22、 (1) 2﹣ ;(2)见解析
【解析】
分析：（1）先求得：∠CAE=45°-15°=30°，根据直角三角形30°角的性质可得AC=2CE=2，再得∠ECD=90°-60°=30°，设ED=x，则CD=2x，利用勾股定理得：x=1，求得x的值，可得BD的长；
（2）如图2，连接CM，先证明△ACE≌△BCF，则∠BFC=∠AEC=90°，证明C、M、B、F四点共圆，则∠BCM=∠MFB=45°，由等腰三角形三线合一的性质可得AM=BM．
详解：（1）∵∠ACB=90°，AC=BC，
∴∠CAB=45°，
∵∠BAD=15°，
∴∠CAE=45°﹣15°=30°，
Rt△ACE中，CE=1，
∴AC=2CE=2，
Rt△CED中，∠ECD=90°﹣60°=30°，
∴CD=2ED，
设ED=x，则CD=2x，
∴CE=x，
∴x=1，
x=，
∴CD=2x=，
∴BD=BC﹣CD=AC﹣CD=2﹣；
（2）如图2，连接CM，
∵∠ACB=∠ECF=90°，
∴∠ACE=∠BCF，
∵AC=BC，CE=CF，
∴△ACE≌△BCF，
∴∠BFC=∠AEC=90°，
∵∠CFE=45°，
∴∠MFB=45°，
∵∠CFM=∠CBA=45°，
∴C、M、B、F四点共圆，
∴∠BCM=∠MFB=45°，
∴∠ACM=∠BCM=45°，
∵AC=BC，
∴AM=BM．

点睛：本题考查了三角形全等的性质和判定、等腰直角三角形的性质和判定、等腰三角形三线合一的性质、直角三角形30°角的性质和勾股定理，第二问有难度，构建辅助线，证明△ACE≌△BCF是关键．
23、（1）20；15%；35%；（2）见解析;（3）126°．
【解析】
（1）根据被调查学生总人数，用B的人数除以被调查的学生总人数计算即可求出m，再根据各部分的百分比的和等于1计算即可求出n；
（2）求出D的学生人数，然后补全统计图即可；
（3）用D的百分比乘360°计算即可得解．
【详解】
解：（1）非常了解的人数为20，
60÷400×100%=15%，
1﹣5%﹣15%﹣45%=35%，
故答案为20；15%；35%；
（2）∵D等级的人数为：400×35%=140，
∴补全条形统计图如图所示：

（3）D部分扇形所对应的圆心角：360°×35%=126°．
【点睛】
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小
24、
【解析】
试题分析：过O作OF垂直于CD，连接OD，利用垂径定理得到F为CD的中点，由AE+EB求出直径AB的长，进而确定出半径OA与OD的长，由OA﹣AE求出OE的长，在直角三角形OEF中，利用30°所对的直角边等于斜边的一半求出OF的长，在直角三角形ODF中，利用勾股定理求出DF的长，由CD=2DF即可求出CD的长．
试题解析：过O作OF⊥CD，交CD于点F，连接OD，
∴F为CD的中点，即CF=DF，
∵AE=2，EB=6，
∴AB=AE+EB=2+6=8，
∴OA=4，
∴OE=OA﹣AE=4﹣2=2，
在Rt△OEF中，∠DEB=30°，
∴OF=OE=1，
在Rt△ODF中，OF=1，OD=4，
根据勾股定理得：DF==，
则CD=2DF=2．

考点：垂径定理；勾股定理．