所属成套资源:人教版数学七年级上册单元测试卷+同步讲练+期中期末测试卷全套(原卷+解析卷)
初中数学人教版七年级上册1.4.1 有理数的乘法精品练习
展开
这是一份初中数学人教版七年级上册1.4.1 有理数的乘法精品练习,文件包含专题14有理数的乘除法讲练-2022-2023七年级上册同步讲练解析版人教版docx、专题14有理数的乘除法讲练-2022-2023七年级上册同步讲练原卷版人教版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
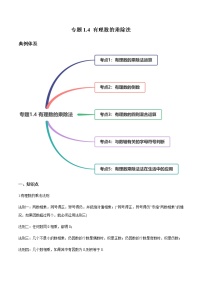
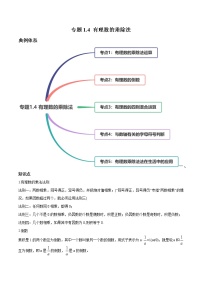
专题1.4 有理数的乘除法
典例体系
一、知识点
1.有理数的乘法法则
法则一:两数相乘,同号得正,异号得负,并把绝对值相乘;(“同号得正,异号得负”专指“两数相乘”的情况,如果因数超过两个,就必须运用法则三)
法则二:任何数同0相乘,都得0;
法则三:几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数;
法则四:几个数相乘,如果其中有因数为0,则积等于0.
2.倒数
乘积是1的两个数互为倒数,其中一个数叫做另一个数的倒数,用式子表示为a·=1(a≠0),就是说a和互为倒数,即a是的倒数,是a的倒数。
注意:①0没有倒数;
②求假分数或真分数的倒数,只要把这个分数的分子、分母点颠倒位置即可;求带分数的倒数时,先把带分数化为假分数,再把分子、分母颠倒位置;
③正数的倒数是正数,负数的倒数是负数。(求一个数的倒数,不改变这个数的性质);
④倒数等于它本身的数是1或-1,不包括0。
3.有理数的乘法运算律
⑴乘法交换律:一般地,有理数乘法中,两个数相乘,交换因数的位置,积相等。即ab=ba
⑵乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。即(ab)c=a(bc).
⑶乘法分配律:一般地,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,在把积相加。即a(b+c)=ab+ac
4.有理数的除法法则
(1)除以一个不等0的数,等于乘以这个数的倒数。
(2)两数相除,同号得正,异号得负,并把绝对值相除。0除以任何一个不等于0的数,都得0
5.有理数的乘除混合运算
(1)乘除混合运算往往先将除法化成乘法,然后确定积的符号,最后求出结果。
(2)有理数的加减乘除混合运算,如无括号指出先做什么运算,则按照‘先乘除,后加减’的顺序进行。
二、考点点拨与训练
考点1:有理数的乘除法运算
典例:(2020·浙江省初三二模)计算:的结果是( )
A. B.12 C.1 D.
【答案】D
【解析】
解:
故选D.
方法或规律点拨
本题考查了有理数的乘法法则,注意符号,熟练掌握乘法法则是解题的关键.
巩固练习
1.(2020·天津初三二模)计算的结果等于( )
A. B.12 C. D.81
【答案】A
【解析】
.
故选:A.
2.(2020·广东省初三其他)计算的结果是( )
A. B.1 C. D.2
【答案】A
【解析】
根据两数相乘异号得负判断符号为负,则=-=-1.
故选A.
3.(2020·四川省初一期末)以下关于0的说法:①0的相反数与0的绝对值都是0;②0的倒数是0;③0减去一个数,等于这个数的相反数;④0除以任何有理数仍得0.其中说法正确的有( )个
A.1 B.2 C.3 D.4
【答案】B
【解析】
解:①0的相反数与0的绝对值都是0,正确;
②0没有倒数,故此项不正确;
③0减去一个数,等于这个数的相反数,正确;
④0除以任何非零有理数仍得0,故此项错误;
综上正确的有①③.
故选:B
4.(2020·天津初三学业考试)计算的值是( )
A.-12 B.-2 C.35 D.-35
【答案】C
【解析】原式
故选:C.
5.(2020·天津初三二模)计算:(﹣3)×5的结果是( )
A.﹣15 B.15 C.﹣2 D.2
【答案】A
【解析】
解:(﹣3)×5=-15,
故选:A.
6.(2020·长沙市一中湘一南湖学校初二月考)若a<c<0<b,则abc与0的大小关系是( )
A.abc<0 B.abc=0
C.abc>0 D.无法确定
【答案】C
【解析】
∵a<c<0<b,
∴abc>0.
故选C.
7.(2017·全国初一课时练习)计算时,应该运用( ).
A.加法交换律 B.乘法分配律
C.乘法交换律 D.乘法结合律
【答案】B
【解析】
∵原式=
=4+3-6
=1
∴应该运用乘法的分配律;
故选B.
8.(2017·全国初一课时练习)计算:(-4)×0.25=__________,(+4)×(-)=______,(-)×(-)=_______.
【答案】-1, -,
【解析】
∵(-4)×0.25=-1,
(+4)×(-)=-,
(-)×(-)=.
故答案为(1). -1, (2). -, (3).
考点2:有理数的倒数
典例:(2020·安徽省初三其他)-5的倒数是( )
A.-5 B.5 C. D.
【答案】D
【解析】
∵
∴-5的倒数是.
故选D.
方法或规律点拨
本题考查了倒数的性质,乘积为”1”的两个数互为倒数.
巩固练习
1.(2020·深圳市龙岗区南湾街道沙湾中学初三其他)-2的倒数是( )
A.-2 B. C. D.2
【答案】B
【解析】
-2的倒数是-
故选B
2.(2020·甘肃省武威市第十中学初三三模)的倒数是( )
A. B. C. D.
【答案】A
【解析】的倒数是,
故选A.
3.(2020·河北省初三学业考试)-2020的倒数是( )
A. B. C.2020 D.
【答案】B
【解析】∵-2020×()=1,
∴-2020的倒数是.
故选:B.
4.(2020·广东省初三其他)6的倒数是( )
A.﹣6 B.6 C. D.﹣
【答案】C
【解析】
6的倒数是,
故选C.
5.(2020·四川省初三)下列选项中,两数互为倒数的是( )
A.5与 B.与 C.2020与 D.2020与
【答案】D
【解析】解:A. 5与互为相反数,而非互为倒数,故该选项与题意不符;
B. 的到数是 ,而的到数是2020,故本选项错误;
C. 2020与互为相反数,而非互为倒数,故该选项与题意不符;
D. 2020与互为倒数,故本选项与题意相符.
故选D.
6.(2020·云南省初三三模)的倒数的绝对值是___________.
【答案】
【解析】的倒数为,的绝对值为
7.(2019·北京市顺义区杨镇第二中学初一期中)﹣1的倒数是__,相反数是__绝对值是__.
【答案】, ,
【解析】
解:∵,
∴﹣1的倒数是,相反数是,绝对值是,
故答案为:,,.
8.(2018·云南省初一期末)已知互为相反数,互为倒数,m的绝对值为3,那么的值是________ .
【答案】2016或1986
【解析】
解:根据题意得:a+b=0,cd=1,m=3或﹣3,
当m=3时,原式=,
当m=﹣3时,原式=,
∴的值为:2016或1986.
故答案为:2016或1986
9.(2019·重庆实验外国语学校初一期中)如果a,b互为相反数,c,d互为倒数,m的绝对值是3,则m2﹣2019a+5cd﹣2019b的值是____.
【答案】14.
【解析】∵a,b互为相反数,c,d互为倒数,m的绝对值是3,
∴a+b=0,cd=1,m=±3,
则m2﹣2019a+5cd﹣2019b
=9﹣2019(a+b)+5cd
=9﹣0+5
=14.
故答案为:14.
考点3:有理数的四则混合运算
典例:(2019·山东省初一期中)学习有理数的乘法后,老师给同学们这样一道题目:计算:49×(-5),看谁算的又快又对,有两位同学的解法如下:
聪聪;原式=-×5=--249;
明明:原式=(49+)×(-5)=49×(-5)+×(-5)=-249,
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:39×(-8).
【答案】(1)明明解法较好;(2)还有更好的解法,解法见解析;(3)﹣319.
【解析】
解:(1)明明解法较好;
(2)还有更好的解法,如下:
原式=(50﹣)×(﹣5)
=﹣250+
=﹣249;
(3)原式=(40﹣)×(﹣8)
=﹣320+
=﹣319.
方法或规律点拨
本题考查了有理数的乘法,主要是对乘法分配律的应用,把带分数进行适当的转化是解题的关键.
巩固练习
1.(2019·北京市顺义区杨镇第二中学初一期中)如图是一个简单的数值运算程序,当输入的x的值为—2时,输出的数值为_________.
【答案】-1
【解析】
当输入-2时,带入程序列式为:(-2)×(-1)-3=2-3=-1.
故答案为:-1.
2.(2020·北京初三月考)对于两个非零整数x,y,如果满足这两个数的积等于它们的和的6倍,称这样的x,y为友好整数组,记作 ,与视为相同的友好整数组.请写出一个友好整数组__________ ,这样的友好整数组一共有__________组 .
【答案】见解析 9
【解析】
由已知可得若为友好整数组,则xy≠0,且xy=6(x+y)
∴(x-6)y=6x,显然当x=6时该等式不成立,
∴x≠6
∴
∵y是整数
∴是整数
∴当x-6=1,即x=7时,y=42,故<7,42>是一个友好整数组.
∵x,y是整数
∴是整数,且x-6是整数
∵xy≠0,且<x,y>与<y,x>视为相同的友好整数组.
∴x-6=±1或±2或±3或±4或-6,
∴这样的友好整数组一共有2+2+2+2+1=9(组).
故答案为:<7,42>;9.
3.利用运算律有时能进行简便计算.
例1
例2
计算:(1);
(2)
【答案】(1);(2)23
【解析】
(1)
;
(2)
.
4.(2019·北京市顺义区杨镇第二中学初一期中)
【答案】-17
【解析】解:原式=
=
=-24+12+9-14
=-17.
5.(2020·成都市金花中学初一期中)用简便方法计算下列各式的值:
(1)
(2)
【答案】(1)-15;(2)0.
【解析】解:
=
=
=
=-15;
(2)
=
=
=0.
6.(2017·全国初一课时练习)学习了有理数的运算后,老师给同学们布置了下面一道题:
计算:,看谁算得又对又快.
下面是甲、乙两名同学给出的解法:
甲:原式= ,
乙:原式=
你认为谁的解法好?你还能想出别的简便方法吗?试一下!
【答案】-
【解析】
乙的解法好,还有方法如下:
原式.
7.(2020·河北省初三一模)计算下列各式的值.
(1)(﹣53)+(+21)﹣(﹣69)﹣(+37)
(2)﹣3.61×0.75+0.61×+(﹣0.2)×75%.
【答案】(1)0;(2)-2.4
【解析】
解:(1)(﹣53)+(+21)﹣(﹣69)﹣(+37)
=﹣53+21+69﹣37
=﹣90+90
=0;
(2)
=﹣3.61×0.75+0.61×0.75+(﹣0.2)×0.75
=0.75×(﹣3.61+0.61﹣0.2)
=0.75×(﹣3.2)
=﹣2.4.
8.(2019·吉林省东北师大附中初一月考)已知、为有理数,现规定一种新运算,满足.
(1)_________;
(2)求的值.
(3)新运算是否满足加法交换律,若满足请说明理由:若不满足,请举出一个反例.
【答案】(1)-6;(2);(3)不满足,举例见解析
【解析】
解:(1)(-2)×4-(-2)=-8+2=-6
(2)
(3)∵新运算
∴运用加法加法交换律可得:
假设,
则=3×4-3=9
=4×3-4=8
∴不能用交换律.
考点4:与数轴有关的字母符号判断
典例:(2020·北京初三二模)实数a,b,c,d在数轴上对应的点的位置如图所示,下列结论正确的是( )
A.|a|0 C.a+c>0 D.d-a>0
【答案】D
【解析】
由实数a,b,c,d在数轴上对应的点的位置可知,a<b<0<c<d,
∴|a|>|b|,ad<0,a+c<0,d-a>0,
因此选项D正确,
故选:D.
方法或规律点拨
本题考查数轴表示数,有理数的四则运算法则,理解符号、绝对值是确定有理数的必要条件.
巩固练习
1.(2020·山西省初一期末)如图所示,A.B两点在数轴上表示的数分别为、,下列式子成立的是( )
A. B. C. D.
【答案】C
【解析】∵a<0,b>0,
∴,故A选项错误;
∵a<b,
∴,故B选项错误;
∵-a>0,b>0,,
∴ ,故C选项正确;
∵a<0,b>0,,
∴,故D选项错误.
故选C.
2.(2020·全国初一)如图,在数轴上,实数的对应点分别为点,则( )
A.1.5 B.1 C. D.
【答案】C
【解析】解:由数轴得a=-0.5,b=2,
∴ab=(-0.5)×2=-1.
故选:C
3.(2020·河北省初三学业考试)如图,在数轴上表示点的倒数的点可能是( )
A.点 B.点 C.点 D.点
【答案】A
【解析】
由图可得,点P在0到1之间且靠近1,则表示点的倒数的点可能在1到2之间,即点A.
故选:A.
4.(2020·山东省济宁学院附属中学初三二模)实数a、b在数轴上的对应点的位置如图所示,则正确的结论是( )
A.a<﹣1 B.ab>0 C.a﹣b<0 D.a+b<0
【答案】C
【解析】选项A,从数轴上看出,a在﹣1与0之间,
∴﹣1<a<0,
故选项A不合题意;
选项B,从数轴上看出,a在原点左侧,b在原点右侧,
∴a<0,b>0,
∴ab<0,
故选项B不合题意;
选项C,从数轴上看出,a在b的左侧,
∴a<b,
即a﹣b<0,
故选项C符合题意;
选项D,从数轴上看出,a在﹣1与0之间,
∴1<b<2,
∴|a|<|b|,
∵a<0,b>0,
所以a+b=|b|﹣|a|>0,
故选项D不合题意.
故选:C.
5.(2020·北京初三二模)实数,,在数轴上的对应点的位置如图所示,则下列结论正确的是( )
A. B. C. D.
【答案】D
【解析】解:由题意得:
A错误,B错误,C错误,D正确.
故选D.
6.(2020·江西省初一期末)有理数a,b在数轴上的表示如图所示,则下列结论中:①ab<0;②ab>0;③a+b<0;④a﹣b<0;⑤a<|b|;⑥﹣a>﹣b,正确的有( )
A.3个 B.4个 C.5个 D.6个
【答案】A
【解析】
由数轴得b
相关试卷
这是一份人教版七年级上册第四章 几何图形初步4.3 角4.3.1 角精品习题,文件包含专题43角讲练-2022-2023学年七年级上册同步讲练解析版人教版docx、专题43角讲练-2022-2023学年七年级上册同步讲练原卷版人教版docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。
这是一份人教版七年级上册2.2 整式的加减精品随堂练习题,文件包含专题22整式的加减讲练-2022-2023七年级上册同步讲练解析版人教版docx、专题22整式的加减讲练-2022-2023七年级上册同步讲练原卷版人教版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
这是一份初中数学2.1 整式优秀练习题,文件包含专题21整式讲练-2022-2023七年级上册同步讲练解析版人教版docx、专题21整式讲练-2022-2023七年级上册同步讲练原卷版人教版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。