高中8.6 空间直线、平面的垂直综合训练题

这是一份高中8.6 空间直线、平面的垂直综合训练题，共40页。

8.6 空间直线、平面的垂直(精练)
【题组一 线面垂直】
1．(2021·全国·高一课时练习)如图，在正方体ABCD﹣A1B1C1D1中，点E是棱BC的中点，点F是棱CD上的动点．当＝__时，D1E⊥平面AB1F．

【答案】1
【解析】连接A1B，则A1B是D1E在面ABB1A内的射影，
∵AB1⊥A1B，∴D1E⊥AB1，
于是D1E⊥平面AB1F，又平面AB1F，所以D1E⊥AF．
连接DE，则DE是D1E在底面ABCD内的射影．
∴D1E⊥AF，，因为，所以平面，
又平面，所以DE⊥AF．
∵ABCD是正方形，E是BC的中点．∴当且仅当F是CD的中点时，DE⊥AF，
即当点F是CD的中点时，D1E⊥平面AB1F．∴＝1时，D1E⊥平面AB1F．故答案为：1.


2．(2021·全国·高一课时练习)如图，四棱锥中，平面，底面是正方形，，F为的中点.求证：平面.

【答案】证明见解析.
【解析】证明：∵平面，平面，∴.
∵四边形是正方形，∴，
又，平面，∴平面，
∵平面，∴.
∵，∴，
又，平面，∴平面.
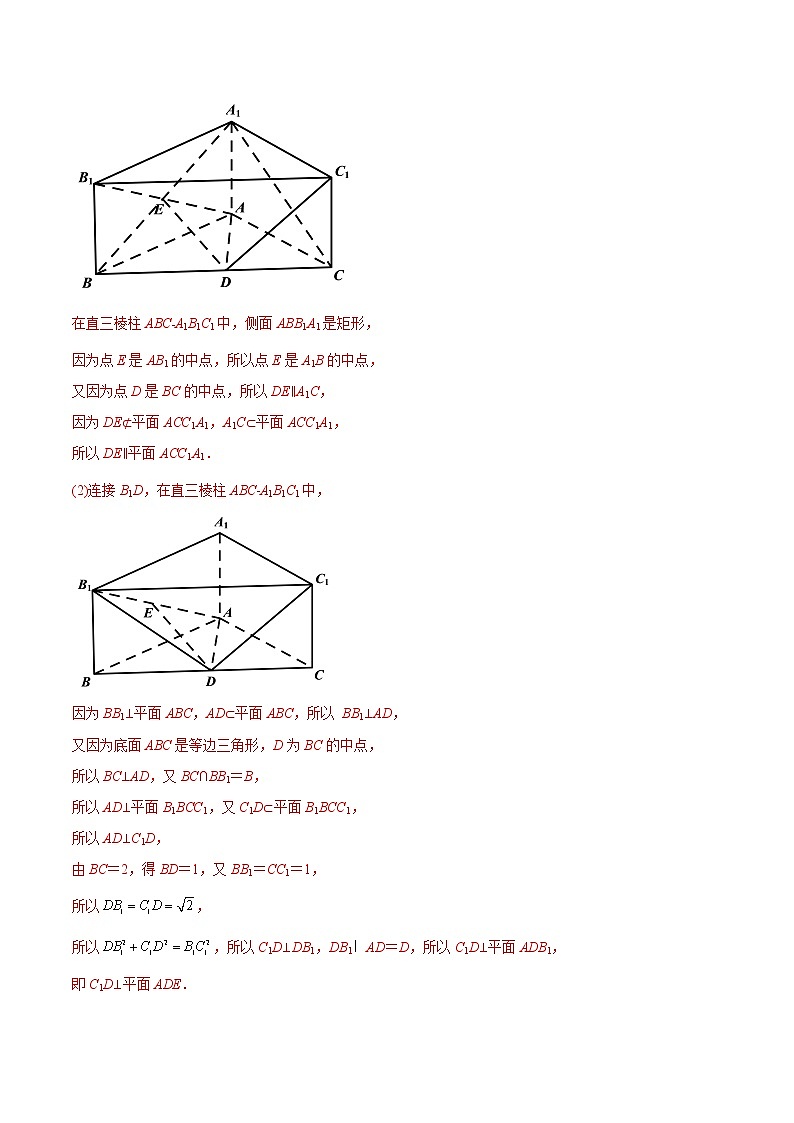
3．(2021·全国·高一单元测试)如图，直三棱柱ABC﹣A1B1C1中，底面是边长为2的等边三角形，点D，E分别是BC，AB1的中点．

(1)证明：DE∥平面ACC1A1；
(2)若BB1＝1，证明：C1D⊥平面ADE．
【答案】(1)证明见解析；(2)证明见解析.
【解析】(1)连接A1B，A1C，

在直三棱柱ABC﹣A1B1C1中，侧面ABB1A1是矩形，
因为点E是AB1的中点，所以点E是A1B的中点，
又因为点D是BC的中点，所以DE∥A1C，
因为DE⊄平面ACC1A1，A1C⊂平面ACC1A1，
所以DE∥平面ACC1A1．
(2)连接B1D，在直三棱柱ABC﹣A1B1C1中，

因为BB1⊥平面ABC，AD⊂平面ABC，所以 BB1⊥AD，
又因为底面ABC是等边三角形，D为BC的中点，
所以BC⊥AD，又BC∩BB1＝B，
所以AD⊥平面B1BCC1，又C1D⊂平面B1BCC1，
所以AD⊥C1D，
由BC＝2，得BD＝1，又BB1＝CC1＝1，
所以，
所以，所以C1D⊥DB1，DB1AD＝D，所以C1D⊥平面ADB1，
即C1D⊥平面ADE．
4．(2021·全国·高一课时练习)如图1，在直角梯形中，，E是的中点，O是与的交点．将沿折起到图2中的位置，得到四棱锥．求证：平面．

【答案】证明见解析
【解析】证明：在题图1中，
因为，E是的中点，，所以．
所以在题图2中，，，
又，所以平面，
又，所以平面．
5．(2021·广西·桂平市麻垌中学高一月考)如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠ABC=60°，PA⊥平面ABCD，点M、N分别为BC、PA中点，且PA=AB=2.


(1)证明：BC⊥平面AMN；
(2)求三棱锥N-AMC的体积；
(3)在线段PD上是否存在一点E，使得MN∥平面ACE；若存在，求出PE的长；若不存在，说明理由.
【答案】(1)详解见解析；(2)；(3)存在点E为PD的中点，PE=
【解析】(1)证明：因为ABCD为菱形，所以AB=BC，
又∠ABC=60°，所以AB=BC=AC，
又M为BC中点，所以BC⊥AM ，
又PA⊥平面ABCD，BC⊂平面ABCD，故PA⊥BC
又PA∩AM=A，所以BC⊥平面AMN.
(2)由(1)知为等边三角形，AB=BC=AC=2
又M为BC中点，则BM=CM=1，故
因此，
又PA⊥平面ABCD，PA=2，N为PA的中点，故AN=1
所以.
(3)存在点E，
取PD中点E，连接NE，EC，AE，如图所示：

因为N，E分别为PA，PD中点，所以，且，
又在菱形ABCD中，，且，
所以，且，即MCEN是平行四边形，故，
又平面ACE，NM平面ACE，故平面ACE，
即在PD上存在一点E，使得MN平面ACE，此时PE=PD=


【题组二 面面垂直】
1．(2021·全国·高一单元测试)如图，四棱锥的底面是边长为a的菱形，平面平面，为的中点.

求证：平面平面.
【答案】证明见解析
【解析】如图所示，设，连接，则.
，
.
∵平面平面，平面平面，
平面平面.
又平面，
故平面平面.

2．(2021·山西省长治市第二中学校高一月考)如图，在三棱锥中，，平面．

(1)求证：平面平面
(2)若，求二面角的正切值
【答案】(1)证明见解析；(2)．
【解析】(1)平面

，平面 平面
平面平面，
平面平面.
(2)设是的中点，过于，连接
在中

平面平面平面，
平面
又平面
是二面角的平面角．
设，则在中，
，
所以.
3．(2021·内蒙古包头·高一期末)如图，在四棱锥中，已知底面是菱形，且对角线与相交于点.

(1)若，求证：平面平面；
(2)设点为的中点，在棱上是否存在点，使得∥平面？请说明理由.
【答案】(1)证明见解析；(2)存在，理由见解析.
【解析】
证明：(1)连接，底面为菱形，.
又
又平面.
平面，平面平面.
(2)棱上存在点，且为的中点，使得∥平面，
证明如下：
连接.
是的中点，∥
平面，平面,∥平面
4．(2021·广东白云·高一期末)如图，垂直于所在的平面，为的直径，，，，，点为线段上一动点.

(1)证明：平面平面；
(2)当点移动到点时，求与平面所成角的正弦值.
【答案】(1)证明见解析；(2).
【解析】(1)证明：因为垂直于所在的平面，即平面，平面，
所以，又为的直径，所以，
因为，所以平面，
又平面，所以，
因为，，
所以平面，又平面，
所以平面平面.
(2)解：因为，，所以，
又，所以，
由，可得，
如图，过点作交于点，则，可得，
又，所以，
所以，，
设点到平面的距离为，
由，可得，解得，
所以当点移动到点时，与平面所成角的正弦值为.

5．(2021·江苏·吴江汾湖高级中学高一月考)如图，在四棱锥中，四边形为矩形，，，分别为，的中点．

(1)求证：平面；
(2)若，求证：平面平面．
【答案】(1)证明见解析；(2)证明见解析.
【解析】(1)连结，

由已知，为和的中点，
又为的中点，．
平面，平面，平面．
(2)，，，平面．
平面，．
，，平面．
平面，∴平面平面．
6(2021·山西·太原市第五十六中学校高一月考)在四棱锥中，底面ABCD是矩形，平面ABCD，，，以BD的中点O为球心，BD为直径的球面交PD于点M.

(1)求直线BD与平面PAD所成的角的正切值；
(2)求证：平面平面PCD.
【答案】(1)；(2)证明见解析.
【解析】(1)∵ 平面ABCD，平面ABCD，
∴ PA⊥BA，
又底面ABCD是矩形，∴BA⊥AD，
又PA，AD平面PAD，,
∴ BA⊥平面PAD，∴ 直线BD与平面PAD内的投影为AD，
∴ 即为直线BD与平面PAD所成的角，
又 AB=2，AD=4，
∴ ；
∴ 直线BD与平面PAD所成的角的正切值为，
(2)证明：依题设，M在以BD为直径的球面上，则，
由(1)得平面PAD，又平面
∴
∵ ，AB，BM平面ABM，
∴ 平面ABM，
又平面
∴ 平面平面PCD.
7．(2021·江苏如皋·高一月考)如图，在四棱锥中，经过AB的平面与PD､PC分别交于点E与点F，且平面平面PCD，，平面ABFE.

(1)求证：；
(2)求证：平面平面PCD.
【答案】(1)证明见解析；(2)证明见解析.
【解析】(1)平面ABFE，平面PCD，平面平面

同理.
(2)由(1)知，，
平面平面PCD，，
平面平面，平面ABFE
平面PCD，又平面PAD中，
平面平面.
8．(2021·江苏·滨海县八滩中学高一期中)如图，在三棱锥中，分别为棱的中点，已知，且．

(1)求证：平面平面；
(2)求直线与平面所成角的正弦值．
【答案】(1)证明见解析；(2)．
【解析】(1)证明：分别为中点，为的中位线
，且，
，
又F为中点，为的中位线，
又，，
又，平面
又平面，所以平面平面
(2)由(1)知平面，又平面，平面平面
因为为中点，
又平面平面，所以平面
为直线与平面所成角，
在直角中，，
所以

9(2021·江苏如皋·高一月考)在直三棱柱中，是的中点，是上一点，线段与相交于点，且平面.

(1)证明：点为线段的中点；
(2)若，证明：平面平面.
【答案】(1)证明见解析；(2)证明见解析.
【解析】(1)设，连接，
因为平面，平面，平面平面
所以，
在直三棱柱中，四边形为平行四边形
所以
因为，所以，即点为线段的中点.
(2)在直三棱柱中，
因为为线段的中点，所以
又因为，是的中点，所以，
因为，所以
在直三棱柱中，平面，平面
所以，因为，，
平面，平面，
所以平面，
因为平面，所以平面平面.

【题组三 线线垂直】
1．(2021·安徽·六安市裕安区新安中学高一期末)如图，在长方体ABCD－A1B1C1D1的棱中，与棱AB垂直的棱有( )

A．2条 B．4条
C．6条 D．8条
【答案】D
【解析】在长方体ABCD－A1B1C1D1的棱中，与棱AB垂直的棱有BC，B1C1，A1D1，AD，AA1，BB1，CC1，DD1，共8条．故选：D.
2．(2021·全国·高一课时练习)如图所示，在空间四边形ABCD中，AD=BC=2，E，F分别是AB，CD的中点，EF=．求证：AD⊥BC．

【答案】证明见解析
【解析】证明：如图所示，取BD的中点H，连接EH，FH．
因为E是AB的中点，且AD=2，

所以EH∥AD，EH=1．同理FH∥BC，FH=1．
所以∠EHF(或其补角)是异面直线AD，BC所成的角．
因为EF=，所以EH2+FH2=EF2，
所以EFH是等腰直角三角形，EF是斜边，
所以∠EHF=90°，即AD与BC所成的角是90°，
所以AD⊥BC．
3．(2021·全国·高一单元测试)如图，已知矩形CDEF和直角梯形ABCD，AB∥CD，∠ADC＝90°，DE＝DA，M为AE的中点.

(1)求证：AC∥平面DMF；
(2)求证：BE⊥DM.
【答案】(1)证明见解析；(2)证明见解析.
【解析】(1)如图，连结EC交DF于点N，连结MN.

因为CDEF为矩形，所以EC，DF相互平分，所以N为EC的中点.
又因为M为EA的中点，所以MN∥AC.
又因为AC⊄平面DMF，且MN⊂平面DMF.
所以AC∥平面DMF.
(2)因为矩形CDEF，所以CD⊥DE.
又因为∠ADC＝90°，所以CD⊥AD.
因为DE∩AD＝D，DE，AD⊂平面ADE，所以CD⊥平面ADE.
又因为DM⊂平面ADE，所以CD⊥DM.
又因为AB∥CD，所以AB⊥DM.
因为AD＝DE，M为AE的中点，所以AE⊥DM.
又因为AB∩AE＝A，AB，AE⊂平面ABE，所以MD⊥平面ABE.
因为BE⊂平面ABE，所以BE⊥MD.
4．(2021·天津红桥·高一学业考试)如图，在三棱锥P- ABC中，PA⊥底面ABC，BC⊥AC，M、N分别是BC、PC的中点.

(1)求证：MN//平面PAB；
(2)求证：BC⊥PC.
【答案】(1)证明见解析；(2)证明见解析.
【解析】(1)因为M、N分别是BC、PC 的中点，
所以，
又平面，
平面，
则平面
(2)因为PA⊥底面ABC，
且 平面ABC，
所以，
又，
且，平面
所以平面，
又平面，
所以BC⊥PC.
5．(2021·全国·高一课时练习)如图，在三棱锥中，底面分别是的中点．

(1)求证：；
(2)求证：平面；
(3)求证：．
【答案】(1) 证明见解析；(2)证明见解析 ；(3) 证明见解析．
【解析】(1)在三棱锥中，因为分别是的中点，
根据三角形的中位线定理，可得．
(2)由(1)知，因为平面，且平面，
根据线面垂直的判定定理，可得平面．
(3)因为平面，且平面，所以，
又因为，且，所以平面，
又由平面，所以．
6．(2021·广西·桂平市麻垌中学高一月考)如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．求证：

(1)AC⊥PB；
(2)PB//平面AEC.
【答案】(1)证明见解析；(2)证明见解析.
【解析】(1)四棱锥P-ABCD中，因PA⊥平面ABCD，AC平面ABCD，于是得AC⊥PA，
而AB⊥AC，，平面PAB，从而得AC⊥平面PAB，又PB平面PAB，
所以AC⊥PB；
(2)连接BD交AC于点O，连接EO，如图，

因底面ABCD为平行四边形，则有O是BD中点，又E是PD中点，于是得EO//PB，而EO平面AEC，PB平面AEC，所以PB//平面AEC.
【题组四 线线角】
1．(2021·黑龙江·嫩江市第一中学校高一期末)如图，空间四边形ABCD的对角线AC＝8，BD＝6，M，N分别为AB，CD的中点，并且异面直线AC与BD所成的角为90°，则MN＝( )

A．3 B．4
C．5 D．6
【答案】C
【解析】取AD的中点P，连接PM，PN，则BD∥PM，AC∥PN，
∴∠MPN或其补角即异面直线AC与BD所成的角，
∴∠MPN＝90°，PN＝AC＝4，PM＝BD＝3，∴MN＝5．

故选：C.
2．(2021·全国·高一课时练习)已知正四棱锥P-ABCD，PA＝2，AB＝，M是侧棱PC的中点，且BM＝，则异面直线PA与BM所成角为________．
【答案】45°
【解析】如图，连接AC，BD交于点O，连接OM，则∠OMB为异面直线PA与BM所成角．由O，M分别为AC，PC中点，得OM＝PA＝1．在RtAOB中，易得OB＝AB·tan·45°＝1．又BM＝，即OB2＋OM2＝BM2，所以OMB为直角三角形，且∠OMB＝45°．

故答案为：45°.
3．(2021·全国·高一课时练习)如图，在三棱柱ABC－A1B1C1中，AA1⊥AB，AA1⊥AC．若AB＝AC＝AA1＝1，BC＝，则异面直线A1C与B1C1所成的角为____．

【答案】60°
【解析】依题意，得BC∥B1C1，故异面直线A1C与B1C1所成的角即BC与A1C所成的角．连接A1B，在A1BC中，BC＝A1C＝A1B＝，故∠A1CB＝60°，即异面直线A1C与B1C1所成的角为60°．

故答案为：60°.
4．(2021·全国·高一课时练习)在正三棱柱ABC－A1B1C1中，D是AB的中点，则在所有的棱中与直线CD和AA1都垂直的直线有______．

【答案】AB，A1B1
【解析】由正三棱柱的性质可知与直线CD和AA1都垂直的直线有AB，A1B1．
故答案为：AB，A1B1.
5．(2021·全国·高一课时练习)若∠AOB＝135°，直线a∥OA，a与OB为异面直线，则a和OB所成的角的大小为______.
【答案】45°
【解析】因为直线OA，a与OB为异面直线，
所以的补角为a与OB所成角，
又,
所以a与OB所成角的大小为.
故答案为：
6．(2021·全国·高一课时练习)如图，在四面体中，，与所成的角为，、分别为、的中点，则线段的长为________．

【答案】或
【解析】取的中点，连接、，

、分别为、的中点，且，
同理可得且，
为异面直线与所成的角或其补角，则或.
在中，.
若，则为等边三角形，此时，；
若，由余弦定理可得.
综上所述，或.
故答案为：或.
7．(2021·全国·高一课时练习)如图所示，空间四边形中，两条对边，分别是另外两条对边上的点，且，则异面直线和所成角的大小为___________.

【答案】
【解析】如图，过点作，交于点，连接

则
异面直线和所成角即为或其补角
在中，，，又
异面直线和所成角的大小为
故答案为：
8．(2021·全国·高一课时练习)如图所示，AB是圆O的直径，点C是弧AB的中点，D、E分别是VB、VC的中点，求异面直线DE与AB所成的角.

【答案】45°.
【解析】因为D、E分别是VB、VC的中点，
所以BC∥DE，因此∠ABC是异面直线DE与AB所成的角，
又因为AB是圆O的直径，点C是弧AB的中点，
所以△ABC是以∠ACB为直角的等腰直角三角形，
于是∠ABC＝45°，
故异面直线DE与AB所成的角为45°.
【题组五 线面角】
1(2021·黑龙江·鸡西实验中学高一期中)如图，四棱锥的底面是平行四边形，底面，，


(1)证明：AC⊥CD；
(2)若E是棱PC的中点，求直线AD与平面PCD所成的角
【答案】(1)证明见解析(2)
【解析】(1)证明：因为底面，底面，所以，
因为，所以，，平面，
所以平面，因为平面，所以．
(2)由(1)平面，平面，所以，，
因为，为的中点，所以，因为，平面，所以平面，所以即为直线与平面所成的角，因为，所以，，所以，所以，因为，所以，即直线与平面所成的角为；
2．(2021·全国·高一课时练习)如图，在棱长均为1的直三棱柱ABC-A1B1C1中，D是BC的中点.

(1)求证:AD⊥平面BCC1B1;
(2)求直线AC1与平面BCC1B1所成角的正弦值.
【答案】(1)证明见解析；(2).
【解析】(1)直三棱柱ABC-A1B1C1中，BB1⊥平面ABC，∴BB1⊥AD，∵AB=AC，D是BC的中点，
∴AD⊥BC.又BC∩BB1=B，∴AD⊥平面BCC1B1.

(2)连接C1D.由(1)AD⊥平面BCC1B1，则∠AC1D即为直线AC1与平面BCC1B1所成角.
在中，AD=，AC1=，sin∠AC1D=，
即直线AC1与平面BCC1B1所成角的正弦值为.
3．(2021·全国·高一课时练习)如图在四棱锥中，底面是边长为的正方形，侧面底面，且，设分别为的中点．

(1)求证：平面；
(2)求证：平面平面；
(3)求直线与平面所成角的大小．
【答案】(1)证明见解析 ；(2) 证明见解析；(3) ．
【解析】(1)因为四边形为正方形，连接，则为中点，为中点，所以在中，且平面，
平面，所以平面．
(2)因为平面平面，
平面平面，且四边形为正方形，
所以平面，
所以平面，所以，
又，
所以是等腰直角三角形，且，
即，且平面，
所以平面，
又平面，所以平面平面．
(3)因为，

所以直线与平面所成角的大小等于直线与平面所成角的大小，
因为侧面底面，所以就是直线与平面所成角，在中，，所以，所以直线与平面所成角的大小为．
4．(2021·浙江·镇海中学高一期中)如图，在直三棱柱中，．

(1)求证：；
(2)若与的所成角的余弦值为，求与平面所成角的正弦值．
【答案】(1)证明见解析；(2)或
【解析】(1)将棱分别向下延长，使得，
连接，如图：

，与的交点为的中点，
，，
，
又，，
平面，
取的中点，连接，
,
平面，
,
又，
平面，
，
又为的中点，
，
，
，，
，

(2)由(1)知与的所成角即与的所成角，，
取的中点，连接，

，
与平面所成的角即为与平面所成的角，
当时，
设，则，
，
由(1)知，为的中点，故，
，
，
令，则，
，
，
又，则，
，
又为等腰三角形，所以，
又，，易得为与平面所成的角，
，，
，

；
当时，设，则，
，
，
，
则，
，，
；
故与平面所成角的正弦值为或
5．(2021·河北邢台·高一月考)如图，在直三棱柱中，底面是的等腰直角三角形，，是边的中点．

(1)证明：平面．
(2)求直线与平面所成角的正弦值．
【答案】(1)证明见解析；(2)．
【解析】(1)证明：因为，为的中点，所以．
又平面，平面，则．
因为，平面，所以平面；
(2)解：由(1)知，平面，平面，
所以．
可求出，，，
所以，
．
设点到平面的距离为，

由，得，
即，解得，即点到平面的距离为．
设与平面所成角为，则，即与平面所成角的正弦值为．
【题组六 二面角】
1．(2021·全国·高一课时练习)如图所示，在△中，平面垂直平分，且分别交于点D，E，，求二面角的大小．

【答案】．
【解析】∵E为的中点，且，
∴．又，
∴面，又面，
∴，
∵面，面，
∴，又，
∴面，面，即，
∴即为二面角的平面角．
设．由，得．
在△中，，即，．
在中，，故，即二面角的大小为．
2．(2021·广东揭东·高一期末)如图，是圆的直径，点是圆上异于，的点，直线平面．

(1)证明：平面平面；
(2)若点是的中点，在上找一点使得直线平面，并说明理由．
(3)设，，求二面角的余弦值．
【答案】(1)证明见解析；(2)点为的中点，证明见解析；(3)．
【解析】(1)证明：是圆的直径，，
又平面，平面，，
，且，平面，平面，
又平面，
平面平面；
(2)为的中点，证明如下：
证明：取的中点，由于点为的中点，
所以，
因为平面，平面，
所以平面；

(3)平面，平面，，
过作于，连结，
，且，平面，
平面，从而得，
为二面角的平面角，
在中，，，
，则，
二面角的余弦值为．
3．(2021·河北·衡水市第十四中学高一期末)在四棱锥中，，，平面，，分别为，的中点，．

(1)求证：平面平面；
(2)求二面角的余弦值．
【答案】(1)证明见解析；(2).
【解析】(1)由题意，设，则，，，
∴，又平面，面，
∴，则在△中，，
在△中，，则，又面，有，
又，故有面，又，分别为，的中点，即，
∴面，又面，则平面平面；
(2)过作，易知为中点，若是中点，连接，
∴，，，故面，即是二面角的平面角，
∴由图知：二面角为，
易知，则面，面，所以，
在△中，，，则，
∴，则二面角的余弦值为.

4．(2021·湖南·武冈市第二中学高一月考)如图，在四棱锥中，，，，，为锐角，平面平面.

(1)证明：平面；
(2)若与平面所成角的正弦值为，求二面角的余弦值.
【答案】(1)证明见解析；(2).
【解析】
(1)证明：在平面内过作于，
因为平面平面，又平面平面，
所以平面，平面，所以，
过分别作于，
取中点为，则，且，
所以四边形是平行四边形，，
所以，
所以， ，
，且平面，所以平面，平面
所以，因为，，平面.
(2)二面角的平面角与二面角的平面角互补，
由(1)可得，平面，因为平面，所以，
所以为二面角的平面角，连接，
在中，为与平面所成的角，由其正弦值为，，
可得，因为，所以，所以，
所以二面角的余弦值为.

5．(2021·浙江衢州·高一期末)如图，平行四边形ABCD中，∠BAD=60°， AB=2，AD=4，将ACBD沿BD翻折到△EBD的位置

(1)当平面EBD⊥平面ABD时，求证：AB⊥DE；
(2)若点F为BE的中点，二面角E-BD-C的大小为60°，求直线DF与平面BCE所成角的正弦值.
【答案】(1)证明见解析；(2).
【解析】(1)证明：在，∠BAD=60°， AB=2，AD=4，所以由余弦定理得


所以，所以
所以AB⊥BD，
因为平面EBD⊥平面ABD，平面EBD∩平面ABD=BD，平面
所以.AB⊥平面EBD，
因为平面EBD，所以AB⊥DE；
(2)因为四边形ABCD为平行四边形，所以∥，
因为AB⊥BD，
所以CD⊥BD，ED⊥BD，
所以二面角E- BD- C的平面角为∠CDE=60°，
因为DC= DE，所以△CDE为正三角形，
连接CE，取CE中点G，连接DG，
则DG⊥CE，在△BCE中，BC=BE，
所以BG⊥CE，BG∩DG=G，
所以CE⊥平面DBG，
因为平面BCE，所以平面BCE⊥平面DBG， .
因为平面BCE∩平面DBG=BG，
作DH⊥BG，则DH⊥平面BCE，连接FH，
则∠DFH是直线DF与平面BCE所成的角

在△DFH中，DF= 2，DH =
∴sin∠DFH=
6(2021·江苏连云港·高一期末)在三棱柱中，，，，．

(1)求二面角的余弦值；
(2)求证：平面平面．
【答案】(1)；(2)证明见解析．
【解析】(1)连接，在中，，，，则，
故，得，则，
在中，，，，则，，，
中，，，，
所以，取的中点为，连接，，则，，
所以为平面与平面所成的二面角，
在中，，得，
，，
所以二面角的余弦值为．
(2)由(1)知，，，，所以平面与平面所成的二面角为，
在中，，，，所以，故，
所以平面与平面所成的二面角为，
所以平面平面．