广东省2022届高三数学二模试卷及答案

 高三数学二模试卷

一、单选题

1．已知集合，则（　　）

A． B． C． D．

2．定义在上的下列函数中，既是奇函数，又是增函数的是（　　）

A． B． C． D．

3．已知随机变量，若，则（　　）

A．0.7 B．0.4 C．0.3 D．0.2

4．某校安排高一年级（1）～（5）班共5个班去A，B，C，D四个劳动教育基地进行社会实践，每个班去一个基地，每个基地至少安排一个班，则高一（1）班被安排到A基地的排法总数为（　　）

A．24 B．36 C．60 D．240

5．若函数与图象的任意连续三个交点构成边长为4的等边三角形，则正实数（　　）

A． B．1 C． D．π

6．赵爽弦图（如图1）中的大正方形是由4个全等的直角三角形和中间的小正方形拼接而成的，若直角三角形的两条直角边长为a，b，斜边长为c，由大正方形面积等于4个直角三角形的面积与中间小正方形的面积之和可得勾股定理．仿照赵爽弦图构造如图2所示的菱形，它是由两对全等的直角三角形和中间的矩形拼接而成的，设直角三角形的斜边都为1，其中一对直角三角形含有锐角，另一对直角三角形含有锐角（位置如图2所示）．借鉴勾股定理的推导思路可以得到结论（　　）

A．

B．

C．

D．

7．已知抛物线E：，圆F：，直线l：（t为实数）与抛物线E交于点A，与圆F交于B，C两点，且点B位于点C的右侧，则△FAB的周长可能为（　　）

A．4 B．5 C．6 D．7

8．存在函数使得对于都有，则函数可能为（　　）

A． B．

C． D．

二、多选题

9．已知复数z的共轭复数是，，i是虚数单位，则下列结论正确的是（　　）

A．

B．的虚部是0

C．

D．在复平面内对应的点在第四象限

10．吹气球时，记气球的半径r与体积V之间的函数关系为r（V），为r（V）的导函数．已知r（V）在上的图象如图所示，若，则下列结论正确的是（　　）

A．

B．

C．

D．存在，使得

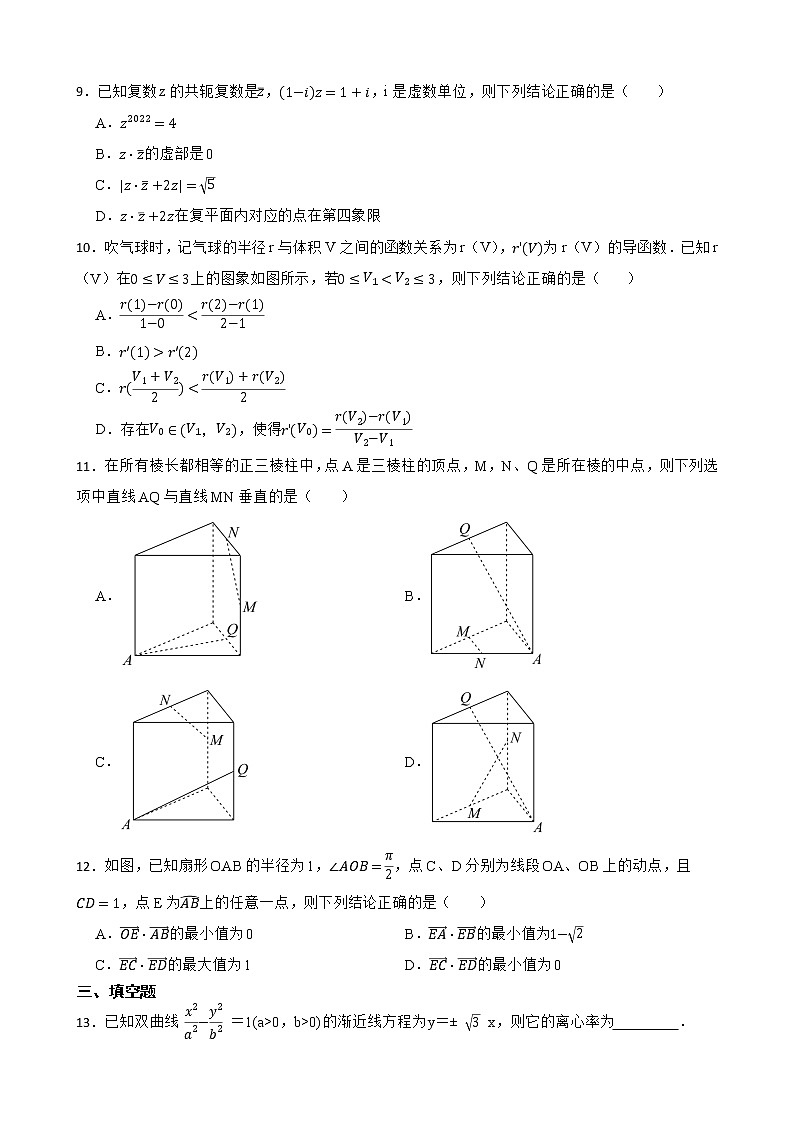
11．在所有棱长都相等的正三棱柱中，点A是三棱柱的顶点，M，N、Q是所在棱的中点，则下列选项中直线AQ与直线MN垂直的是（　　）

A． B．

C． D．

12．如图，已知扇形OAB的半径为1，，点C、D分别为线段OA、OB上的动点，且，点E为上的任意一点，则下列结论正确的是（　　）

A．的最小值为0 B．的最小值为

C．的最大值为1 D．的最小值为0

三、填空题

13．已知双曲线 ＝1(a>0，b>0)的渐近线方程为y＝± x，则它的离心率为　     　．  

14．若直线和直线将圆的周长四等分，则　     　．

15．若函数的最大值为1，则常数的一个取值为　                                                   　．

16．十字贯穿体（如图1）是美术素描学习中一种常见的教具．如图2，该十字贯穿体由两个全等的正四棱柱组合而成，且两个四棱柱的侧棱互相垂直，若底面正方形边长为2，则这两个正四棱柱公共部分所构成的几何体的内切球的体积为　     　．

四、解答题

17．已知递增等比数列的前n项和为，且满足，．

（1）求数列的通项公式．

（2）若数列满足，求数列的前15项和．

18．小李下班后驾车回家的路线有两条．路线1经过三个红绿灯路口，每个路口遇到红灯的概率都是；路线2经过两个红绿灯路口，第一个路口遇到红灯的概率是，第二个路口遇到红灯的概率是．假设两条路线全程绿灯时的驾车回家时长相同，且每个红绿灯路口是否遇到红灯相互独立．

（1）若小李下班后选择路线1驾车回家，求至少遇到一个红灯的概率．

（2）假设每遇到一个红灯驾车回家时长就会增加1min，为使小李下班后驾车回家时长的累计增加时间（单位：min）的期望最小，小李应选择哪条路线？请说明理由．

19．如图，已知△ABC内有一点P，满足．

（1）证明：．

（2）若，，求PC．

20．如图1，在△ABC中，，DE是△ABC的中位线，沿DE将△ADE进行翻折，使得△ACE是等边三角形（如图2），记AB的中点为F．

（1）证明：平面ABC．

（2）若，二面角D-AC-E为，求直线AB与平面ACD所成角的正弦值．

21．已知椭圆C：，点为椭圆的右焦点，过点F且斜率不为0的直线交椭圆于M，N两点，当与x轴垂直时，．

（1）求椭圆C的标准方程．

（2），分别为椭圆的左、右顶点，直线，分别与直线：交于P，Q两点，证明：四边形为菱形．

22．已知函数（且）的图象与x轴交于P，Q两点，且点P在点Q的左侧．

（1）求点P处的切线方程，并证明：时，．

（2）若关于x的方程（t为实数）有两个正实根，证明：．

答案解析部分

1．【答案】C

2．【答案】D

3．【答案】A

4．【答案】C

5．【答案】C

6．【答案】B

7．【答案】B

8．【答案】D

9．【答案】B,C

10．【答案】B,D

11．【答案】A,C

12．【答案】B,C,D

13．【答案】2

14．【答案】2

15．【答案】（答案不唯一，取，均可）

16．【答案】

17．【答案】（1）解：设的公比为q，则由，得．

整理得．

又，得．

联立得，消去，得．

解得或．

又因为为递增等比数列，

所以，．

所以．

（2）解：（方法一）当时，，则，，同理，列举得，，，，，，，．

记的前n项和为，则

．

所以数列的前15项和为92．

（方法二）由，

得，

记的前n项和为，则

．

所以数列的前15项和为92．

18．【答案】（1）解：设路线1遇到红灯的个数的随机变量为X，则，

所以至少遇到一个红灯的事件为，

由对立事件概率公式，

得，

所以若小李下班后选择路线1驾车回家，至少遇到一个红灯的概率为．

（2）解：设路线1累计增加时间的随机变量为，则，

所以，

设路线2第i个路口遇到红灯为事件（，2），则，，

设路线2累计增加时间的随机变量为，则的所有可能取值为0，1，2，则

，

，

，

所以．

因为，

所以为使小李下班后驾车回家时长的累计增加时间的期望最小，小李应选择路线1．

19．【答案】（1）证明：在△ABP中，由正弦定理得，

即，

要证明，只需证明，

在△ABP中，，

在△ABC中，，

所以，

所以，

所以．

（2）解：由（1）知，又因为，，

所以，

由已知得△ABC为等腰直角三角形，所以，

则，

所以在△PBC中，，

由正弦定理得，

即，

即．

由余弦定理得，

由题意知，

故解得，

所以．

20．【答案】（1）证明：如图，

取AC中点G，连接FG和EG，由已知得，且．

因为F，G分别为AB，AC的中点，所以，且

所以，且．

所以四边形DEGF是平行四边形．

所以．

因为翻折的，易知．

所以翻折后，．

又因为，EA，平面AEC，

所以平面AEC．

因为，

所以平面AEC．

因为平面AEC，所以．

因为ACE是等边三角形，点G是AC中点，所以

又因为，AC，平面ABC．

所以平面ABC．

因为，所以平面ABC．

（2）解：（方法一）如图，

过点E作，以E为原点，EH、EC，ED所在直线分别为x，y，z轴，建立空间直角坐标系E-xyz，设，则，，，，则，，，

因为平面AEC．所以是平面AEC的法向量，

设面ACD的法向量为，则

，即，解得．

取，得．

因为二面角D-AC-E为，所以，

解得，所以，．

记直线AB与平面ACD所成角为，

则，

所以直线AB与平面ACD所成角的正弦值为．

（方法二）如图，

连接DG，因为平面AEC，平面AEC，所以．

又因为，，DE，平面DEG．所以平面DEC．

因为EG，平面DEG，所以，，所以∠DGE是二面角D-AC-E的平面角，故．

由△ACE是边长为2的等边三角形，得，

在RtDGE中，，所以，．

过点F作，垂足为I，

因为平面DEGF，平面ACD，所以平面平面ACD．

又因为平面平面，平面DEGF，且，

所以平面ACD．

连接AI，则∠FAI即为直线AB与平面ACD所成的角．

在Rt△DFG中，，，得，由等面积法得，解得．

在RtAFG中，，，所以．

在RtFAI中，，

所以直线AB与平面ACD所成角的正弦值为．

21．【答案】（1）解：由题可知．

当与x轴垂直时，不妨设M的坐标为，

所以，

解得，．

所以椭圆C的标准方程为．

（2）证明：设的方程为，，，

联立得消去x，得，

易知恒成立，由韦达定理得，，

由直线的斜率为，得直线的方程为，

当时，，

由直线的斜率为，得直线的方程为，

当时，，

若四边形为菱形，则对角线相互垂直且平分，下面证，

因为，

代入韦达定理得

，

所以，即PQ与相互垂直平分，所以四边形为菱形．

22．【答案】（1）证明：令，得．

所以或．

即或．

因为点P在点Q的左侧，所以，．

因为，

所以，得点P处的切线方程为，即．

当时，，

因为，且，所以，所以，即．

所以，

所以．

（2）证明：不妨设，且只考虑的情形．

因为，所以．

所以点Q处的切线方程为，记，

令，，

设，则．

所以单调递增．

又因为，

所以，当时，；当时，．

所以在上单调递减，在上单调递增．

所以在时有极小值，也是最小值，

即，所以当时，．

设方程的根为，则．

易知单调递增，由，所以．

对于（1）中，设方程的根为，则．

易知单调递减，由（1）知，所以．

所以．

因为，易知时，，故；当时，，所以，

所以，

所以．

记，，则恒成立．

所以单调递增，因为，，

所以存在使得．

所以，当时．；当时，．

所以在上单调递减，在上单调递增．

因为，，由函数图象知当方程（t为实数）有两个正实根时，，

所以．

所以，

即．