数学22.1.1 二次函数精品一课一练

第22章 重点突破训练：与二次函数有关的纯数学问题

考点体系

考点1：二次函数与面积问题

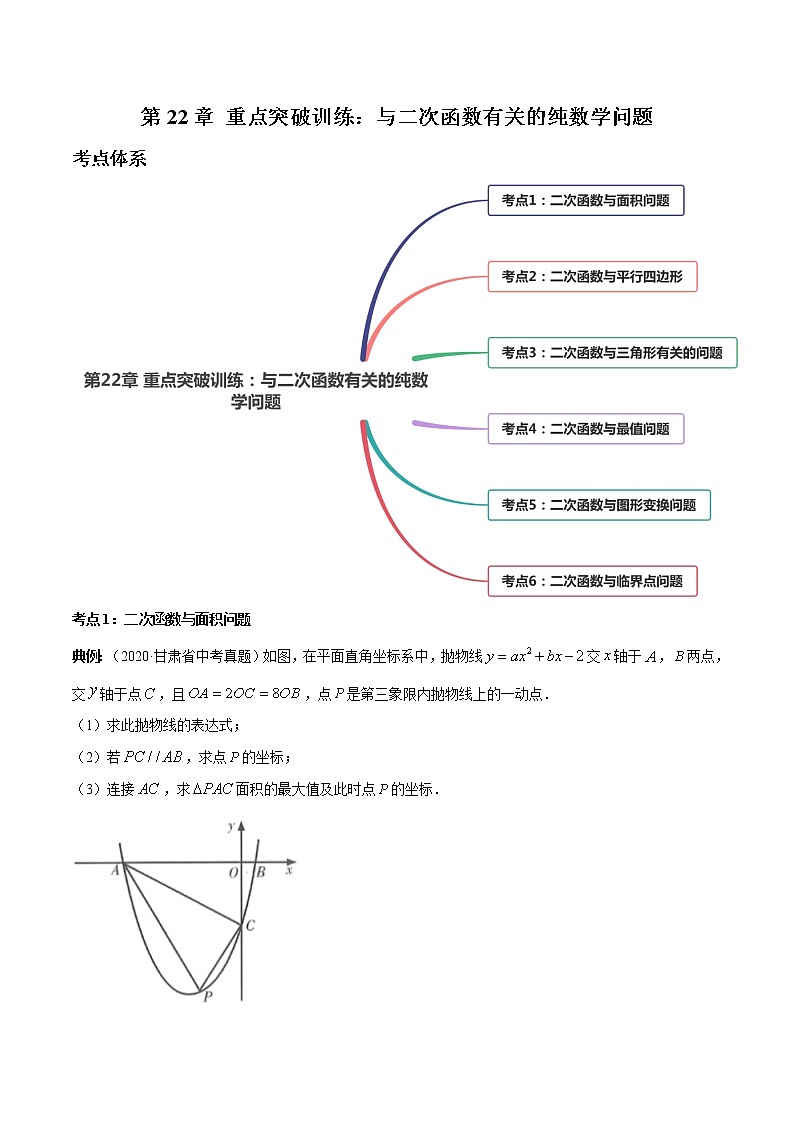
典例：（2020·甘肃省中考真题）如图，在平面直角坐标系中，抛物线交轴于，两点，交轴于点，且，点是第三象限内抛物线上的一动点．

（1）求此抛物线的表达式；

（2）若，求点的坐标；

（3）连接，求面积的最大值及此时点的坐标．

方法或规律点拨

本题考查了二次函数的综合问题，二次函数的性质，一次函数的性质，解题的关键是熟练掌握二次函数和一次函数的性质进行解题，注意利用数形结合的思想进行解题．

巩固练习

1．（2020·内蒙古自治区初三期末）如图,已知直线y=-2x+3与抛物线y=x2相交于A,B两点,O为坐标原点.

(1)求点A和B的坐标；

(2)连结OA,OB,求△OAB的面积.

2．（2020·广西壮族自治区初三其他）已知，如图，抛物线的顶点为，经过抛物线上的两点和的直线交抛物线的对称轴于点．

（1）求抛物线的解析式和直线的解析式．

（2）在抛物线上两点之间的部分（不包含两点），是否存在点，使得？若存在，求出点的坐标；若不存在，请说明理由．

（3）若点在抛物线上，点在轴上，当以点为顶点的四边形是平行四边形时，直接写出满足条件的点的坐标．

3．（2020·安徽省初三月考）已知，如图，抛物线经过点和.

（1）求此抛物线和直线AB的函数表达式；

（2）点P是直线AB下方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为F，交直线AB于点E，作于点D.动点P在什么位置时，的面积最大？求出面积的最大值，并求出此时点P的坐标.

4．（2020·张家界市民族中学初三月考）如图，已知抛物线经过A（－3，0），B（1，0），C（0，3）三点，其顶点为D，对称轴是直线l，l与x轴交于点H．

（1）求该抛物线的解析式；

（2）若点P是该抛物线对称轴l上的一个动点，求△PBC周长的最小值；

（3）如图（2），若E是线段AD上的一个动点（ E与A、D不重合），过E点作平行于y轴的直线交抛物线于点F，交x轴于点G，设点E的横坐标为m，△ADF的面积为S．

①求S与m的函数关系式；

②S是否存在最大值？若存在，求出最大值及此时点E的坐标； 若不存在，请说明理由．

考点2：二次函数与平行四边形

典例：（2020·眉山市东坡区苏辙中学初三其他）如图所示，平面直角坐标系中，直线y＝﹣x+3交坐标轴与B、C两点，抛物线y＝ax2+bx+3经过B、C两点，且交x轴于另一点A（﹣1，0）．点D为抛物线在第一象限内的一点，过点D作DQ∥CO，DQ交BC于点P，交x轴于点Q．

（1）求抛物线解析式；

（2）设点P的横坐标为m，在点D的移动过程中，存在∠DCP＝∠DPC，求出m值；

（3）在抛物线取点E，在坐标系内取点F，问是否存在以C、B、E、F为顶点且以CB为边的矩形？如果有请求出点E的坐标；如果不存在，请说明理由．

方法或规律点拨

本题考查了等腰三角形的性质，矩形的性质，待定系数法求函数解析式，一次函数与坐标轴的交点，二次函数的图像与性质，以及分类讨论的数学思想，熟练掌握各知识点是解答本题的关键．

巩固练习

1．（2020·广西壮族自治区中考真题）已知抛物线与x轴交于点A，B两点（A在B的左侧）与y轴交于点C．

（1）直接写出点A，B，C的坐标；

（2）将抛物线经过向下平移，使得到的抛物线与x轴交于B， 两点（在B的右侧），顶点D的对应点，若，求的坐标和抛物线的解析式；

（3）在（2）的条件下，若点Q在x轴上，则在抛物线或上是否存在点P，使以为顶点的四边形是平行四边形？如果存在，求出所有符合条件的点P的坐标；如果不存在，请说明理由．

2．（2020·内蒙古自治区初三期末）如图，在直角坐标系中，点A的坐标为(-2，0)，OB=OA，且∠AOB=120°．

(1)求经过A、O、B三点的抛物线的解析式；

(2)在(1)中抛物线的对称轴上是否存在点C，使△OBC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由；

(3)若点M为抛物线上一点，点N为对称轴上一点，是否存在点M、N使得A、O、M、N构成的四边形是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．

3．（2020·辽宁省初三其他）如图1，在平面直角坐标系中，抛物线交轴于、两点，交轴于点，且、．

（1）求该抛物线的表达式及顶点的坐标；

（2）若点是轴上的一个动点，设的面积为，动点的坐标为，令，当时，是否有最小值？若有，请求出的最小值和此时的值；若没有，请说明理由；

（3）在抛物线上有一个动点，轴上有一个动点，使得以、、、为顶点的四边形是平行四边形，请直接写出点的坐标．

4．（2020·甘肃省中考真题）如图所示，抛物线与轴交于、两点，与轴交于点，且点的坐标为，点的坐标为，对称轴为直线.点是抛物线上一个动点，设点的横坐标为，连接，，，．

（1）求抛物线的函数表达式；

（2）当的面积等于的面积的时，求的值；

（3）在（2）的条件下，若点是轴上一动点，点是抛物线上一动点，试判断是否存在这样的点，使得以点为顶点的四边形是平行四边形．若存在，请直接写出点的坐标；若不存在，请说明理由．

考点3：二次函数与三角形有关的问题

典例：（2020·陕西省中考真题）如图，抛物线y＝x2+bx+c经过点（3，12）和（﹣2，﹣3），与两坐标轴的交点分别为A，B，C，它的对称轴为直线l．

（1）求该抛物线的表达式；

（2）P是该抛物线上的点，过点P作l的垂线，垂足为D，E是l上的点．要使以P、D、E为顶点的三角形与△AOC全等，求满足条件的点P，点E的坐标．

方法或规律点拨

本题主要考查了二次函数与几何运用，涉及到三角形全等，掌握数形结合思想是解答关键，其中（2）需要分类求解，避免遗漏．

巩固练习

1．（2020·广东省初三月考）如图，抛物线y＝x2＋bx＋c过点A(3，0)，B(1，0)，交y轴于点C，点P是该抛物线上一动点，点P从C点沿抛物线向A点运动(点P不与A重合)，过点P作PD∥y轴交直线AC于点D．

（1）求抛物线的解析式；

（2）求点P在运动的过程中线段PD长度的最大值；

（3）△APD能否构成直角三角形？若能，请直接写出所有符合条件的点P坐标；若不能，请说明理由．

2．（2020·江苏省初三一模）如图，已知二次函数的图像与坐标轴交于点和点．

（1）求该二次函数的解析式；

（2）已知该函数图像的对称轴上存在一点，使得的周长最小．请求出点的坐标；

（3）在（2）的条件下，在轴上找一点，使得是等腰三角形，请直接写出所有符合条件的点的坐标．

3．（2020·江苏省中考真题）如图，在平面直角坐标系中，函数的图像交轴于点、，交轴于点，它的对称轴交轴于点．过点作轴交抛物线于点，连接并延长交轴于点，交抛物线于点．直线交于点，交抛物线于点，连接、．

                                          备用图            

（1）点的坐标为：______；

（2）当是直角三角形时，求的值；

（3）与有怎样的位置关系？请说明理由．

4．（2020·湖南省中考真题）如图1所示，在平面直角坐标系中，抛物线与轴交于点和点，与轴交于点．

（1）求抛物线的表达式；

（2）如图2，将抛物线先向左平移1个单位，再向下平移3个单位，得到抛物线，若抛物线与抛物线相交于点，连接，，．

①求点的坐标；

②判断的形状，并说明理由；

（3）在（2）的条件下，抛物线上是否存在点，使得为等腰直角三角形，若存在，求出点的坐标；若不存在，请说明理由．

5．（2020·山东省中考真题）如图，抛物线交x轴于，两点，与y轴交于点C，AC，BC．M为线段OB上的一个动点，过点M作轴，交抛物线于点P，交BC于点Q．

（1）求抛物线的表达式；

（2）过点P作，垂足为点N．设M点的坐标为，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？

（3）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．

考点4：二次函数与最值问题

典例：11．（2020·重庆初三二模）如图，抛物线与轴交于两点，与轴交于点，过点作∥x轴交抛物线于点，连接

（1）求这个抛物线的解析式

（2）设为抛物线上的一点，且在直线的下方，连接，当的面积最大时，线段在轴上左右移动得到线段，求的最小值．

方法或规律点拨

此题主要考查二次函数综合，解题的关键是熟知待定系数法、三角形的面积公式、对称性及二次函数的图像性质．

巩固练习

1．（2020·平江县南江中学初三二模）如图，在平面直角坐标系xOy中，抛物线y = ax2+ bx + c经过A、B、C三点，已知点A（-3，0），B（0，3），C（1，0）．

（1）求此抛物线的解析式；

（2）点P是直线AB上方的抛物线上一动点，（不与点A、B重合），过点P作x轴的垂线，垂足为F，交直线AB于点E，作PD⊥AB于点D．动点P在什么位置时，△PDE的周长最大，求出此时P点的坐标；

（3）在直线x = -2上是否存在点M，使得∠MAC = 2∠MCA，若存在，求出M点坐标．若不存在，说明理由．

2．（2020·北京中考真题）小云在学习过程中遇到一个函数．下面是小云对其探究的过程，请补充完整：

（1）当时，对于函数，即，当时，随的增大而      ，且；对于函数，当时，随的增大而      ，且；结合上述分析，进一步探究发现，对于函数，当时，随的增大而        ．

（2）当时，对于函数，当时，与的几组对应值如下表：

综合上表，进一步探究发现，当时，随的增大而增大．在平面直角坐标系中，画出当时的函数的图象．

（3）过点(0，m)（）作平行于轴的直线，结合（1）（2）的分析，解决问题：若直线与函数的图象有两个交点，则的最大值是   ．

3．（2020·湖南省中考真题）在平面直角坐标系中，关于的二次函数的图象过点，．

（1）求这个二次函数的表达式；

（2）求当时，的最大值与最小值的差；

（3）一次函数的图象与二次函数的图象交点的横坐标分别是和，且，求的取值范围．

4．（2020·湖南省初三一模）如图，已知抛物线(a≠0)的对称轴为直线，且抛物线经过A(1，0)，C(0，3)两点，与轴交于点B．

（1）若直线经过B，C两点，求直线BC和抛物线的解析式；

（2）在抛物线的对称轴上找一点M，使MA+MC的值最小，求点M的坐标；

（3）设P为抛物线的对称轴上的一个动点，求使ΔBPC为直角三角形的点P的坐标．

考点5：二次函数与图形变换问题

典例：（2020·浙江省初三学业考试）如图，在平面直角坐标系中，二次函数 的图象交 轴于点 ， （点 在点 的左侧），与 轴交于点 ，函数图象的点顶为点 ．

（1）求点 ， 的坐标，并根据该函数图象写出当 时 的取值范围；

（2）将点 向上平移 个单位到点 ，过点 作 轴的平行线，与二次函数的图象交于点 ，，若 ，求 的值．

方法或规律点拨

本题考查了二次函数的性质，二次函数图象上点的坐标特征，坐标与图形的性质，熟练掌握二次函数的性质是解题的关键．

巩固练习

1．（2020·湖南省中考真题）如图，抛物线与轴交于，两点．

（1）若过点的直线是抛物线的对称轴．

①求抛物线的解析式；

②对称轴上是否存在一点，使点关于直线的对称点恰好落在对称轴上．若存在，请求出点的坐标；若不存在，请说明理由．

（2）当，时，函数值的最大值满足，求的取值范围．

2．（2020·北京初三三模）在平面直角坐标系xOy中，二次函数y=ax2﹣2ax+c的图象经过点A（﹣1，1），将A点向右平移3个单位长度，再向上平移2个单位长度，得到点B，直线y=2x+m经过点B，与y轴交于点C．

（1）求点B，C的坐标；

（2）求二次函数图象的对称轴；

（3）若二次函数y=ax2﹣2ax+c（﹣1＜x＜2）的图象与射线CB恰有一个公共点，结合函数图象，直接写出a的取值范围．

3．（2020·河北省初三其他）已知抛物线C：y＝ax2﹣2ax+3开口向下．

（1）当抛物线C过点（1，4）时，求a的值和抛物线与y轴的交点坐标；

（2）求二次函数y＝ax2﹣2ax+3的对称轴和最大值（用含a的式子表示）；

（3）将抛物线C向左平移a个单位得到抛物线C1，随着a的变化，抛物线C1顶点的纵坐标y与横坐标x之间存在一个函数关系，求这个函数关系式，并写出自变量x的取值范围；

（4）记（3）所求的函数为D，抛物线C与函数D的图象交于点M，结合图象，请直接写出点M的纵坐标的取值范围．

4．（2020·仪征市实验中学初三三模）如图，已知二次函数y＝ax2＋bx－5（a，b是常数，a0）的图象与x轴交于点A（－1，0）和点B（5，0）．动直线y＝t（t为常数）与抛物线交于不同的两点P、Q（点P在Q的左侧）．

（1）求抛物线的解析式；  

（2）动直线y＝t与y轴交于点C，若CQ=3CP，求t的值；

（3）将抛物线y＝ax2＋bx－5在x轴下方的部分沿x轴翻折，若动直线y＝t与翻折后的图像交于点M、N，点M、N能否是线段PQ的三等分点？若能，求PQ的长度；若不能，请说明理由．

考点6：二次函数与临界点问题

典例：（2020·吉林省初三三模）定义：二次函数y=ax2+bx+c(a≠0)，我们称函数

为它的相关函数．

（1）已知二次函数y=−2x2+x+3

①直接写出它的相关函数的解析式；

②设它的相关函数图像与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，求ΔABC的面积；

（2）已知二次函数y=x2+mx+2的图像经过点(1,1)，求其相关函数的解析式，并直接写出当−2≤x≤0时相关函数y的取值范围．

（3）如图，正方形ABCD的边长为4，AB//x轴，AD//y轴，点A的坐标是(−2,2)，当二次函数y=x2−2x+1−c的相关函数的图像与正方形ABCD的边有3个交点时，直接写出c的取值范围．

方法或规律点拨

本题考查了抛物线与x轴的交点问题，主要考查了待定系数法求二次函数的解析式，二次函数的图象与性质二次函数图象上点的坐标特征，数形结合是解题的关键．

巩固练习

1．（2020·长春市新朝阳实验学校初三月考）定义：对于二次函数，我们称函数为它的分函数（其中为常数）．例如：的分函数为．设二次函数的分函数的图象为．

（1）直接写出图象对应的函数关系式．

（2）当时，求图象在范围内的最高点和最低点的坐标．

（3）当图象在的部分与轴只有一个交点时，求的取值范围．

（4）当，图象到轴的距离为个单位的点有三个时，直接写出的取值范围．

2．（2020·吉林省初三二模）在平面直角坐标系中，将函数为常数)的图象记为图象与直线的交点坐标为．

（1）若点在图象上，求的值；

（2）求的最小值；

（3）当直线的图象与函数为常数)的图像只有一个公共点时，求的取值范围；

（4）若点在图象上，且点的横坐标为点关于轴的对称点为点.当点不在坐标轴上时，以点为顶点构造矩形使点落在轴上.当图象与矩形的边有两个公共点时，直接写出的取值范围．

3．（2020·河北省初三二模）已知点，抛物线与轴从左到右的交点为，．

（1）若抛物线经过点，求抛物线的解析式和顶点坐标；

（2）当时，求的值；

（3）直线经过点，与轴交于点，

①求点的坐标；

②若线段与抛物线有唯一公共点，直接写出正整数的值．

4．（2020·江苏省泰兴市实验初级中学初三二模）在平面直角坐标系中，已知矩形ABCD，AB∥DC∥y轴，B(－1，－2)，D(2，4)．抛物线C：y=a(x－m)2+n(a＞0)的顶点Q在边BC上，与边AB，DC分别相交于点E，F，点H为CD的中点．

（1）若a＝1

①当抛物线C过点H时，求m的值；

②当点F在点H下方，AE=HF时，求m的值；

（2）当m=－1时，求a的取值范围；

（3）若点M 在抛物线C上，求证：点M始终位于轴下方．

5．（2020·吉林省初三月考）在平面直角坐标系中，已知：函数．

（1）当时，

①求随增大而增大时，的取值范围；

②当时，求的取值范围；

③当时，设的最大值与最小值之差为，当时，求的值．

（2）若，连结.当此函数的图象与线段只有两个公共点时，直接写出的取值范围．

6．（2020·吉林大学附属中学初三二模）定义：对于已知的两个函数，任取自变量的一个值，当时，它们对应的函数值相等；当时，它们对应的函数值互为相反数，我们称这样的两个函数互为相关函数.例如：正比例函数，它的相关函数为.

（1）已知点在一次函数的相关函数的图像上，求的值；

（2）已知二次函数.

①当点在这个函数的相关函数的图像上时，求的值；

②当时，求函数的相关函数的最大值和最小值.

（3）在平面直角坐标系中，点、的坐标分别为、，连结.直接写出线段与二次函数的相关函数的图像有两个公共点时的取值范围.