初中23.1 图形的旋转精品精练

专题23.1 图形的旋转

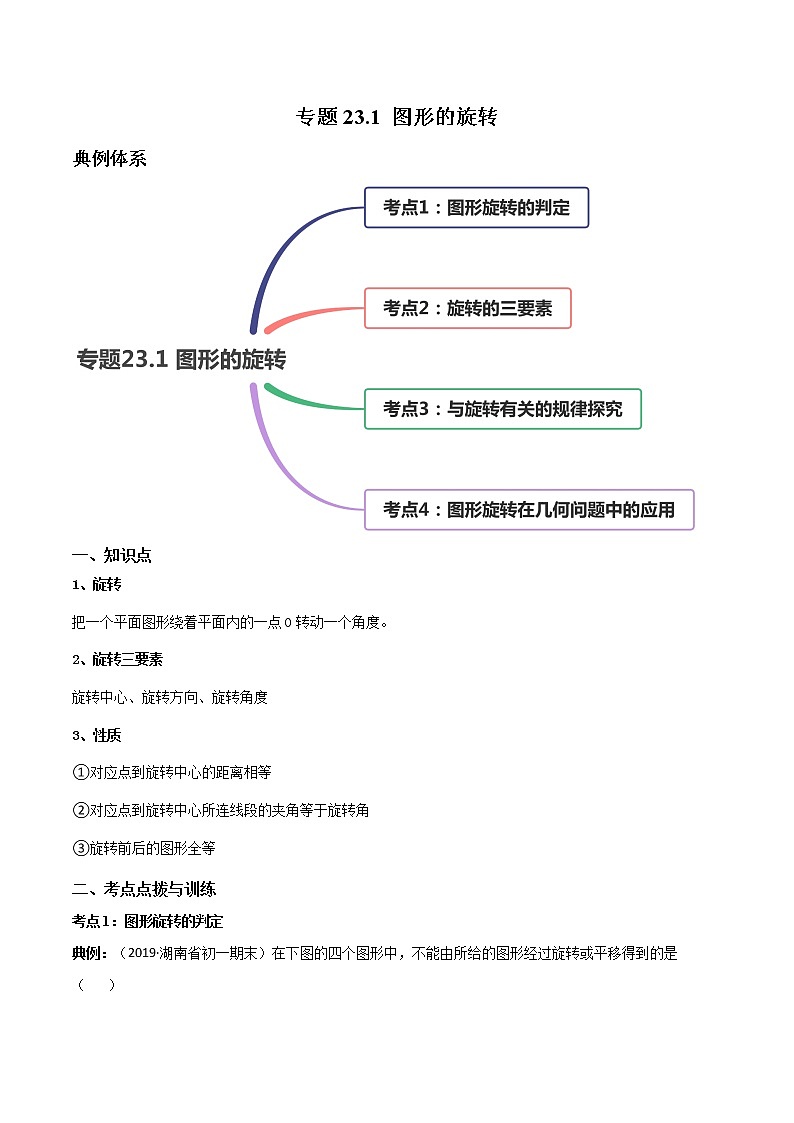
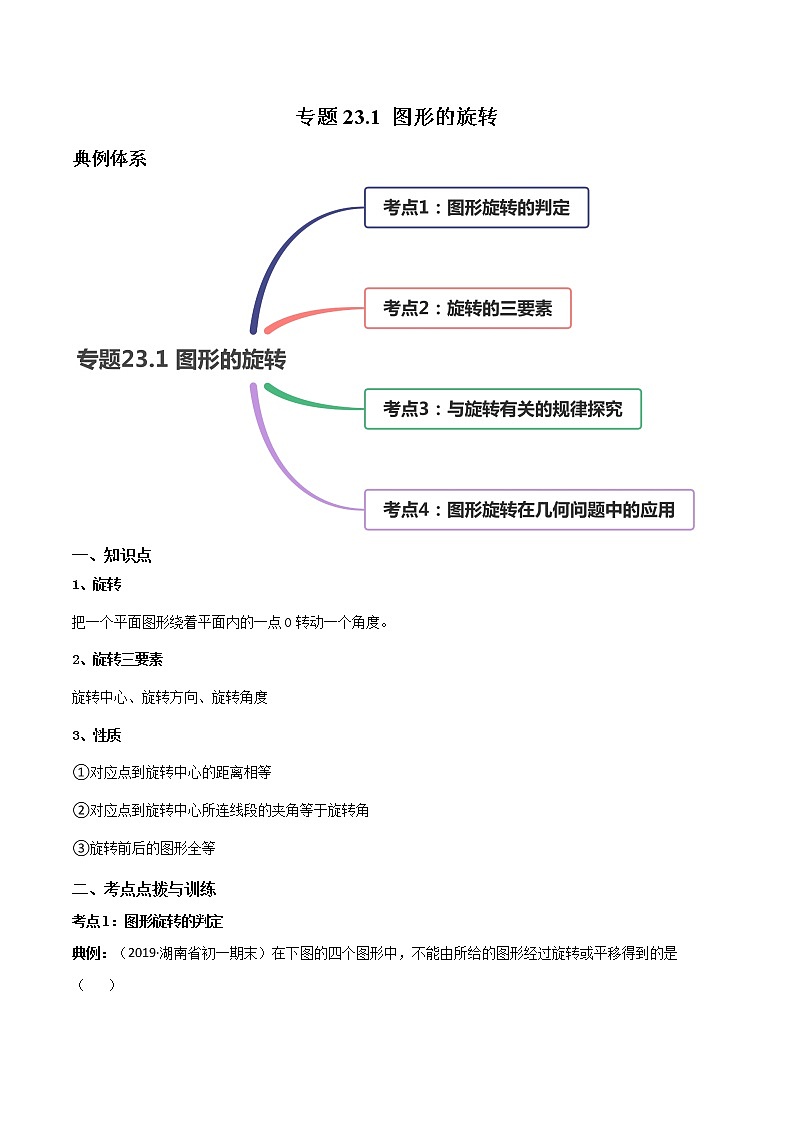
典例体系

一、知识点

1、旋转

把一个平面图形绕着平面内的一点O转动一个角度。

2、旋转三要素

旋转中心、旋转方向、旋转角度

3、性质

①对应点到旋转中心的距离相等

②对应点到旋转中心所连线段的夹角等于旋转角

③旋转前后的图形全等

二、考点点拨与训练

考点1：图形旋转的判定

典例：（2019·湖南省初一期末）在下图的四个图形中，不能由所给的图形经过旋转或平移得到的是（    ）

A． B． C． D．

方法或规律点拨

本题考查平移、旋转的性质．平移的基本性质是：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等；旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变，两组对应点连线的交点是旋转中心．

巩固练习

1．（2020·河南省初三其他）下列运动属于旋转的是（    ）

A．火箭升空的运动 B．足球在草地上滚动 C．大风车运动的过程 D．传输带运输的东西

2．（2020·江阴初级中学初一期中）下列汽车标志中，可以看作由“基本图案”通过平移得到的是(　　)

A． B． C． D．

3．（2018·内蒙古自治区初三期中）4张扑克牌如图（1）所示放在桌子上，小敏把其中两张旋转180°后得到如图（2）所示，那么她所旋转的牌从左起是（ ）

A．第一张、第二张

B．第二张、第三张

C．第三张、第四张

D．第四张、第一张

4．（2019·长春市第一五三中学初三期中）右图中的“笑脸”顺时针旋转270°后得到的图形是（    ）

A． B． C． D．

5．（2019·河北省初一期末）下列四个图形中，不能由下图在同一平面内经过旋转得到的是（    ）

A．① B．② C．③ D．④

6．（2019·山东省初二月考）如图，甲图案变成乙图案，既能用平移，又能用旋转的是                  （   ）

A． B． C． D．

7．（2019·北京市鲁迅中学初三期中）下面生活中的实例,不是旋转的是（    ）

A．传送带传送货物 B．螺旋桨的运动

C．风车风轮的运动 D．自行车车轮的运动

考点2：旋转的三要素

典例：1（2020·扬州市江都区实验初级中学初二期中）在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1，则其旋转中心可能是（　　）

A．点A B．点B C．点C D．点D

方法或规律点拨

此题主要考查旋转中心的确认，解题的关键是熟知旋转的性质特点.

典例：2（2019·湖北省初三期末）如图，在Rt△ACB中，∠ACB＝90°，∠A＝35°，将△ABC绕点C逆时针旋转α角到△A1B1C 的位置，A1B1恰好经过点B，则旋转角α的度数等（ ）

A．70° B．65° C．55° D．35°

方法或规律点拨

本题考查旋转的性质以及等腰三角形的性质．注意掌握旋转前后图形的对应关系是解此题的关键．

典例：3（2020·江西省初三二模）如图，正方形的边长为一个边长为的小正方形沿着正方形的边连续翻转(小正方形起始位置在边上)，当这个小正方形翻转到边的终点位置时，它的方向是（  ）

A． B． C． D．

方法或规律点拨

本题主要考查了生活中的旋转现象，根据题意画出小正方形连续翻转后的草图是解决问题的关键．

巩固练习

1．（2019·山东省鲁村中学初二月考）如图，在Rt△ABC中，∠BAC＝90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C，点A在边B′C上，则∠B′的大小为(  )

A．42° B．48°

C．52° D．58°

2．（2020·广东省初二期中）如图，点A、B、C、D、O都在方格纸的格点上，若△COD是由△AOB绕点O按逆时针方向旋转而得，则旋转的角度为（　　）

A．30° B．45°

C．90° D．135°

3．（2020·内蒙古自治区初三月考）如图，一块含角的直角三角板ABC绕点C顺时针旋转到，当在一条直线上时，三角板ABC的旋转角度为（    ） 

A． B． C． D．

4．（2020·河北省初三其他）如图△ABC绕点A旋转至△ADE，则旋转角是（　　）

A．∠BAD B．∠BAC C．∠BAE D．∠CAD

5．（2020·河北省初三一模）如图，将正五边形绕中心顺时针旋转角度，与原正五边形构成新的图形，若要使该图形既是轴对称又是中心对称图形，则的最小角度为（  ）

A． B． C． D．

6．（2020·内蒙古自治区初三期中）如图，在Rt△ABC中，∠ACB=90°，∠A=40°，以直角顶点C为旋转中心，将△ABC旋转到△EFC的位置，其中E、F分别是A、B的对应点，且点B在斜边EF上，直角边CE交AB于D，则旋转角等于（ ）．

A．70° B．80° C．60° D．50°

7．（2020·山东省初三二模）下列图形中，旋转后可以和原图形重合的是 （　　）

A．正三角形 B．正方形 C．正五边形 D．正六边形

8．（2019·河北省初三月考）如图，在边长为1的正方形网格中，图形是由图形旋转得到的，则旋转中心的坐标为（    ）

A． B． C． D．

9．（2019·山东省初二期中）如图，△DEF是由△ABC绕着某点旋转得到的，则这点的坐标是（　　）

A．（1，1） B．（0，1） C．（﹣1，1） D．（2，0）

10．（2019·浙江省初三期末）如图，在Rt△ABC中，∠BAC=90°，将Rt△ABC绕点C按逆时针方向旋转46°得到Rt△A′B′C，点A在边B′C上，则∠ACB的大小为（    ）

A．23° B．44° C．46° D．54°

11．（2018·上海初一期末）如图，如果正方形ABCD旋转后能与正方形CDEF重合，那么图形所在平面内，可作为旋转中心的点个数（　　）

A．1个 B．2个 C．3个 D．4个

12．（2019·全国初一单元测试）1.下列图案都是在一个图案的基础上，利用“几何画板”软件中变换功能形成的．它们的共性是都可以由一个“基本图案”通过连续旋转得来，旋转的角度是（   ）

A．30 B．45 C．60 D．90

13．（2020·山东省中考真题）如图，已知点A(2，0)，B(0，4)，C(2，4)，D(6，6)，连接AB，CD，将线段AB绕着某一点旋转一定角度，使其与线段CD重合（点A与点C重合，点B与点D重合），则这个旋转中心的坐标为_____．

14．（2020·江苏省初三其他）如图，A点的坐标为（﹣1，5），B点的坐标为（3，3），线段AB绕着某点旋转一个角度与线段CD重合（C、D均为格点），若点A的对应点是点C，且C点的坐标为（5，3），则这个旋转中心的坐标是__________．

15．（2020·江苏省初三其他）如图，若正方形EFGH由正方形ABCD绕图中某点顺时针旋转90°得到，则旋转中心应该是________点.

16．（2019·上海市建虹高级中学初一月考）如图，△ABC顺时针旋转能与△ADE重合，且∠BAE=60°，则旋转中心是__________，旋转角的大小是_________度.

17．（2020·广东省初二期中）如图，AC是正方形ABCD的对角线，△ABC经过旋转后到达△AEF的位置．

(1)指出它的旋转中心；

(2)说出它的旋转方向和旋转角是多少度；

(3)分别写出点A，B，C的对应点．

18．（2018·河南省初二期中）如图，在边长为1的小正方形组成的的方格中，和的顶点都在格点上，且.利用平移、旋转变换，能使通过一次或两次变换后与完全重合.

（1）请你写出通过两次变换与完全重合的变换过程.

（2）通过一次旋转就能得到.请在图中标出旋转中心，并简要说明你是如何确定的.

19．（2020·江苏省初二月考）如图，方格纸上每个小方格的边长都是1，△ABC是通过△A1B1C1旋转得到．

（1）在图中标出旋转中心点O；

（2）画出△ABC向下平移4个单位长度，再向右平移4个单位长度得到的△A2B2C2．

20．（2020·贵州省初三期中）如图，正方形中，经顺时针旋转后与重合．

旋转中心是点________，旋转了________度；

如果，，求：四边形的面积．

考点3：与旋转有关的规律探究

典例：（2020·长春市新朝阳实验学校初三月考）如图，在平面直角坐标系中，为坐标原点，将函数的图象记为，它与轴的交点为、．将绕点旋转180°得到，点的对称点为；将绕点旋转180°得到，点的对称点为；……，按此方法操作，直至得到．若在上，则的值为_________．

方法或规律点拨

本题考查了平面直角坐标系下的二次函数图像旋转和平移变换后的函数关系式的确定方法．解题的关键是注意数形结合．

巩固练习

1．（2020·山东省初三一模）在平面直角坐标系中，点P（a,b）绕点O顺时针旋转45°为一次变换，第2020次变换后得点P′，则点P′的坐标为（      ）

A．（ a, b） B．（-a,-b） C．（b,-a） D．（b,-a）

2．（2020·湖南省初三一模）下面摆放的图案，从第二个起，每个都是前一个按顺时针方向旋转90°得到，第2020个图案中箭头的指向是（　　）

A．上方 B．左方 C．下方 D．右方

3．（2019·石家庄市第十三中学初一期末）如图，一圆桌周围有5个箱子 ，依顺时针方向编号1 ~5 ，小明从1号箱子 沿着圆桌依顺时针方向前进，每经过-个箱子就丢入-颗球，所有小球共有红、黄、绿3种颜色， 1号箱子红色， 2号箱子黄色， 3号箱子绿色， 4号红色， 5号黄色， 1号绿色．．．．． ，颜色依次循环，当他围绕圆桌刚好丢完2020圈时，则第5号箱子有（      ） 个红球．

A．672 B．673 C．674 D．675

4．（2019·全国初一单元测试）有两个完全重合的矩形，将其中一个始终保持不动，另一个矩形绕其对称中心O按逆时针方向进行旋转，每次均旋转45°，第1次旋转后得到图①，第2次旋转后得到图②……则第10次旋转后得到的图形与图①~④中相同的是（    ）.

A．图① B．图② C．图③ D．图④

5．（2018·全国初三单元测试）己知点，将点绕原点顺时针旋转后的对应点为，将点绕原点顺时针旋转后的对应点为，依此作法继续下去，则点的坐标是（ ）

A． B． C． D．

6．（2020·河北省初三二模）如图1，将一个正三角形绕其中心最少旋转，所得图形与原图的重叠部分是正六边形；如图2，将一个正方形绕其中心最少旋转 45°，所得图形与原图形的重叠部分是正八边形；依此规律，将一个正七边形绕其中心最少旋转______，所得图形与原图的重叠部分是正多边形．在图2中，若正方形的边长为，则所得正八边形的面积为_______．

7．（2019·黑龙江省初三三模）如图，在直角坐标系中，已知点的坐标为，将线段按逆时针方向旋转，再将其长度伸长为的倍，得到线段；又将线段按逆时针方向旋转，长度伸长为的倍，得到线段．．．．．．如此下去，得到线段为正整数)，则点的坐标为 __________________．

8．（2020·江西省初三月考）如图，在平面直角坐标系中，正六边形的顶点，．将正六边形绕点顺时针旋转，每秒旋转，则第2018秒时，点的坐标为________．

9．（2020·广西壮族自治区初三三模）已知，⊙A与x轴相切于点O，点A的坐标为（0，1），点P在⊙A上，∠PAO=60°，⊙A沿x轴正方向滚动，当点P第n次落在x轴上时，点P坐标为_____．

考点4：图形旋转在几何问题中的应用

典例：（2020·河北省初三学业考试）如图，在等腰中，，，将绕点逆时针旋转，得到，连结．

（1）求证：；

（2）四边形是什么形状的四边形？并说明理由；

（3）直接写出：当分别是多少度时，①；②．

方法或规律点拨

本题考查了全等三角形的判定和性质，旋转的性质，菱形的判定和性质，灵活运用这些性质解决问题是本题的关键．

巩固练习

1．（2020·北京初二期末）已知：是等边三角形，点D在射线BC上，连接AD，将线段AD绕点A逆时针旋转得到线段 AE，连接EC，作EF // BC交直线AB于点F．

 (1) 当点D在线段BC上时，如图1，

①依据题意，补全图1；

②猜想线段AB，AF，BD的数量关系，并证明；

(2)当点D在线段BC的延长线上时，直接写出线段AB，AF，BD的数量关系．

2．（2020·甘肃省中考真题）如图，点，分别在正方形的边，上，且，把绕点顺时针旋转得到．

（1）求证：≌．

（2）若，，求正方形的边长．

3．（2020·利辛县阚疃金石中学初二月考）如图E是正方形ABCD的边AB 的中点，延长BC到点F，使CF=AE．

（1）若把△ADE绕点D旋转一定的角度时，能否与△CDF重合？请说明理由．

（2）现把△DCF向左平移，使DC与AB重合，得△ABH，AH交ED于G，求证：AH ⊥ED．

4．（2020·湖北省初二期中）如图1，已知正方形的边在正方形的边上，连接、．

（1）试猜想与的数量关系与位置关系；

（2）将正方形绕点按顺时针方向旋转，使点落在边上，如图2，连接和．你认为（1）中的结论是否还成立？若成立，给出证明；若不成立，请说明理由．

5．（2020·江苏省河塘中学初一月考）如图1，已知直线m⊥n，垂足为点O．现有一个直角三角形ABC，其中∠ACB＝90°，∠B＝30°，现将这个三角形按如图方式放置，使得点A与O重合，点C落在直线m上．操作：将△ABC绕点O逆时针旋转一周，如图2所示．通过操作我们发现，当旋转一定角度α时，△ABC会被直线m（或n）分成两个三角形，其中有一个三角形的两角相等．请直接写出所有符合条件的旋转角度α．

6．（2020·河南省实验中学初二月考）如图，Rt△ABC中，∠C=90°，把R△ABC绕着B点逆时针旋转，得到Rt△DBE，点E在AB上 .

(1)若∠BDA=70°，求∠BAC的度数；

(2)若BC=8，AC=6，求△ABD中AD边上的高.