期中考试冲刺卷一九年级上册同步讲练（人教版）

这是一份期中考试冲刺卷一九年级上册同步讲练（人教版），文件包含期中考试冲刺卷一-2022-2023学年九年级上册同步讲练解析版人教版docx、期中考试冲刺卷一-2022-2023学年九年级上册同步讲练原卷版人教版docx、期中考试冲刺卷一-2022-2023学年九年级上册同步讲练答题卡人教版docx等3份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。

期中考试冲刺卷一
一、选择题（本大题共14个小题，每题2分，共28分，在每个小题的四个选项中只有一项是符合题目要求的）
1．（2019·张掖市育才中学期末）下列图形既是轴对称图形，又是中心对称图形的是（ ）
A． B．
C． D．
【答案】D
【解析】A、不是轴对称图形，是中心对称图形，故本选项错误；
B、是轴对称图形，但不是中心对称图形，故本选项错误；
C、是轴对称图形，但不是中心对称图形，故本选项错误；
D、既是轴对称图形，又是中心对称图形，故本选项正确．
故选D．
2．（2019·河北路北·）若关于x的方程（a﹣2）x2﹣3x+a-1＝0是一元二次方程，则（　　）
A．a≠2 B．a＞2 C．a＝0 D．a＞0
【答案】A
【解析】关于x的方程（a﹣2）x2﹣3x+a-1＝0是一元二次方程，得a−2≠0，
所以a≠2.
故选A.
3．（2019·河北路北·）将方程化成一般形式后其二次项系数与常数项分别是（ ）
A． B． C． D．
【答案】A
【解析】解：将方程化成一般形式为：，
则它的二次项系数为3，常数项为−10，
故选：A．
4．（2019·河北路北·）下列函数关系中，是二次函数的是（ ）
A．在弹性限度内，弹簧的长度y与所挂物体质量x之间的关系
B．当距离一定时，火车行驶的时间t与速度v之间的关系
C．等边三角形的周长C与边长a之间的关系
D．圆的面积S与半径R之间的关系
【答案】D
【解析】弹簧长度y=kx+b，是一次函数；
路程=速度×时间=vt，路程一定时，时间与速度成反比，是反比例函数；
三角形周长为三边之和，即C=3a，是一次函数；
根据圆面积公式可得S=πR²，是二次函数.
故选D.
5．（2019·湖北恩施·初三期末）平面直角坐标系内与点P（﹣2，3）关于原点对称的点的坐标是（　　）
A．（3，﹣2） B．（2，3） C．（2，﹣3） D．（﹣3，﹣3）
【答案】C
【解析】解：由题意，得
点P（-2，3）关于原点对称的点的坐标是（2，-3），
故选：C．
6．（2019·河北路北·）若方程x2+mx-3＝0的一根为3，则m等于 （ ）.
A．-2 B．-1 C．1 D．2
【答案】A
【解析】解：∵方程x2+mx-3＝0的一根为3，
∴9+3m-3=0,
解得：m=-2,
故选A.
7．（2019·湖北恩施·初三期末）把y=x2-2x+1写成y=a(x-h)2+k的形式是(　　 )
A．y=(x-2)2-1 B．y=(x-1)2+2 C．y=(x-1)2+ D．y=(x-2)2-3
【答案】A
【解析】解: y=x2-2x+1
=( x2-4x) +1
=( x2-4x+4-4) +1
=(x-2)2-1
故选A.
8．（2019·广东阳东·初三期中）把抛物线y=-x2+2的图象绕原点旋转180°，所得的抛物线的函数关系是( )
A．y=x2+2 B．y=-x2+2 C．y=-x2-2 D．y=x2-2
【答案】D
【解析】抛物线y=-x2+2的顶点坐标为（0，2），
因为二次函数y=-x2+2的图象绕原点旋转180°后得到的抛物线顶点坐标不变，只是开口方向相反，
所以旋转后的抛物线解析式为y=x2-2．
故选D．
9．（2019·河北路北·）一条排水管的截面如下图所示，已知排水管的半径OB=5，水面宽AB=8，则截面圆心O到水面的距离OC是( )

A．4 B．5 C． D．3
【答案】D
【解析】解：由题意可知，OC⊥AB，
∴BC＝AB＝4，
在Rt△OCB中，由勾股定理得：OC＝，
故选D．
10．（2020·黑龙江哈尔滨·初三一模）把抛物线y＝3x2向右平移2个单位，然后向下平移6个单位，则平移后抛物线的解析式为（ ）
A．y＝3（x+2）2+6 B．y＝3（x﹣2）2+6
C．y＝3（x+2）2﹣6 D．y＝3（x﹣2）2﹣6
【答案】D
【解析】抛物线y=3x2向右平移2个单位，得：y=3（x﹣2）2；
再向下平移6个单位，得：y=3（x﹣2）2﹣6．
故选D．
11．（2019·河北路北·）如图，点A是量角器直径的一个端点，点B在半圆周上，点P在上，点Q在AB上，且PB＝PQ．若点P对应135°（45°），则∠PQB的度数为（ ）

A．65° B．67.5° C．60° D．80°
【答案】B
【解析】解：连接OP，如图，则∠AOP＝135°，
∴∠ABP＝∠AOP＝67.5°．
∵PB＝PQ，
∴∠PQB＝∠ABP＝67.5°．
故选：B．

12．（2020·全国初三课时练习）解方程：①；②；③；④．较简便的解法是（ ）
A．依次用直接开平方法、配方法、公式法和因式分解法
B．①用直接开平方法，②用公式法，③④用因式分解法
C．依次用因式分解法、公式法、配方法和因式分解法
D．①用直接开平方法，②③用公式法，④用因式分解法
【答案】D
【解析】①3x2-12=0符合ax2=b（a，b同号且a≠0）的特点所以用直接开平方法；
②3x2-4x-2=0，等号左边有3项，方程的左边利用学过的方法不能分解，所以需要用求根公式法；
③20x2-9x-16=0，等号左边有3项，方程的左边利用学过的方法不能分解，所以需要用求根公式法；
④3（4x-1）2=7（4x-1），可以把4x-1看做是个整体，利用因式分解法解方程，
故选D.
13．（2020·全国初三课时练习）在同一平面直角坐标系内，二次函数与一次函数的图象可能是（ ）
A． B．
C． D．
【答案】C
【解析】解：A、由一次函数图象可知，a＞0，b＞0，由二次函数图象可知，a＞0，b＜0，不符合题意；
B、由一次函数图象可知，a＞0，b＜0，由二次函数图象可知，a＜0，b＜0，不符合题意；
C、由一次函数图象可知，a＞0，b＜0，由二次函数图象可知，a＞0，b＜0，符合题意；
D、由一次函数图象可知，a＜0，b=0，由二次函数图象可知，a＞0，b＜0，不符合题意；
故选：C．
14．（2020·山东东阿·期末）如图所示，在Rt△ABC中，AB＝AC，D、E是斜边BC上的两点，且∠DAE＝45°，将△ADC绕点A按顺时针方向旋转90°后得到△AFB，连接EF，有下列结论：①BE＝DC；②∠BAF＝∠DAC；③∠FAE＝∠DAE；④BF＝DC．其中正确的有（　　）

A．①②③④ B．②③ C．②③④ D．③④
【答案】C
【解析】解：∵△ADC绕A顺时针旋转90°后得到△AFB，
∴△ABF≌△ACD，
∴∠BAF＝∠CAD，AF＝AD，BF＝CD，故②④正确，
∴∠EAF＝∠BAF+∠BAE＝∠CAD+∠BAE＝∠BAC﹣∠DAE＝90°﹣45°＝45°＝∠DAE故③正确
无法判断BE＝CD，故①错误，
故选：C．
二、填空题（本题共4个小题；每个小题3分，共12分，把正确答案填在横线上）
15．（2019·东源县实验中学初三三模）如图，在矩形ABCD中，AD=3，将矩形ABCD绕点A逆时针旋转，得到矩形AEFG，点B的对应点E落在CD上，且DE=EF，则AB的长为_____．

【答案】3
【解析】∵四边形ABCD是矩形，∴∠D=90°，BC=AD=3，
∵将矩形ABCD绕点A逆时针旋转得到矩形AEFG，
∴EF=BC=3，AE=AB，
∵DE=EF，
∴AD=DE=3，
∴AE==3，
∴AB=3，
故答案为3.
16．（2019·河北路北·）已知一条抛物线，以下说法：①对称轴为，当时，随的增大而增大；②；③顶点坐标为；④开口向上.其中正确的是______.（只填序号）
【答案】①④
【解析】因为y=2(x﹣3)2+1是抛物线的顶点式，顶点坐标为(3，1)，
①对称轴为x=3，当x＞3时，y随x的增大而增大，故①正确；
②，故②错误；
③顶点坐标为(3，1)，故③错误；
④∵a=1＞0，
∴开口向上，故④正确．
故答案为：①④．
17．（2019·河北路北·）如图，在平面直角坐标系中，⊙A与y轴相切于原点O，平行于x轴的直线交⊙A于M、N两点，若点M的坐标是（﹣4，﹣2），则弦MN的长为_____．

【答案】3
【解析】分别过点M、N作x轴的垂线，过点A作AB⊥MN，连接AN

设⊙A的半径为r．
则AN=OA=r，AB=2，
∵AB⊥MN，
∴BM=BN，
∴BN=4-r；
则在Rt△ABN中，根据勾股定理，
得AB2+BN2=AN2，即：22+（4-r）2=r2，解得r=2.5，
则N到y轴的距离为1，
又∵点N在第三象限，
∴N的坐标为（-1，-2）；
∴MN=3；
故答案是：3．
18．（2020·全国初三课时练习）如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，水面下降2m，水面宽度增加______m.

【答案】4-4
【解析】建立平面直角坐标系，设横轴x通过AB，纵轴y通过AB中点O且通过C点，则通过画图可得知O为原点，

抛物线以y轴为对称轴，且经过A，B两点，OA和OB可求出为AB的一半2米，抛物线顶点C坐标为
通过以上条件可设顶点式，其中可通过代入A点坐标
代入到抛物线解析式得出：所以抛物线解析式为
当水面下降2米，通过抛物线在图上的观察可转化为：
当时，对应的抛物线上两点之间的距离，也就是直线与抛物线相交的两点之间的距离，
可以通过把代入抛物线解析式得出：
解得：
所以水面宽度增加到米，比原先的宽度当然是增加了
故答案是：
三、解答题（本题共8道题，19-21每题6分，22-25每题8分，26题10分，满分60分）
19．（2019·河北路北·）解下列一元二次方程
（1）用配方法解方程：x2﹣8x+1＝0
（2）用因式分解法解方程：2x2+1＝3x
【答案】(1) x1＝4+，x2＝4﹣;(2) x1＝，x2＝1．
【解析】解：（1）x2﹣8x+1＝0，
配方，得：x2﹣8x+42＝﹣1+42，
即（x﹣4）2＝15，
解这个方程，得：x﹣4＝±，
即x1＝4+，x2＝4﹣．
（2）2x2+1＝3x，
2x2﹣3x+1＝0，
（2x﹣1）（x﹣1）＝0，
解得x1＝，x2＝1．
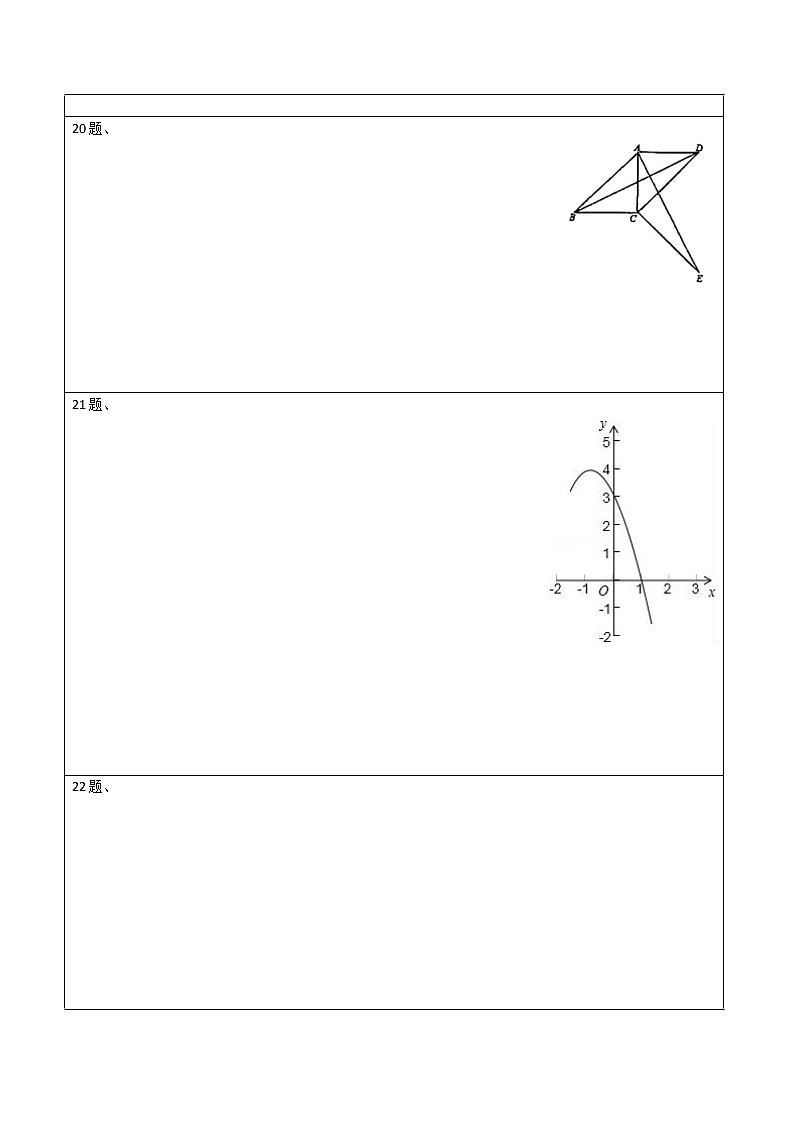
20．（2020·山东东阿·期末）如图，四边形中，，将绕点顺时针旋转一定角度后，点的对应点恰好与点重合，得到.

（1）判断的形状，并说明理由；
（2）若，，试求出四边形的对角线的长.
【答案】（1）是等腰直角三角形，理由详见解析；（2）
【解析】解：（1）是等腰直角三角形.
理由：∵，
∴，
∴，
∴是等腰直角三角形.
（2）如图：由旋转的性质可知：
，，，
∴，，
∵，
∴，
∴，
∴.

21．（2019·河北路北·）如图，已知抛物线y=﹣x2+bx+c的图象经过（1，0），（0，3）两点．
（1）求b，c的值；
（2）写出当y＞0时，x的取值范围．

【答案】（1）b=-2,c=3；（2）当y＞0时，﹣3＜x＜1．
【解析】（1）根据题意，将（1，0）、（0，3）代入，得：

解得：
（2）由（1）知抛物线的解析式为
当y=0时，
解得：或x=1，
则抛物线与x轴的交点为
∴当y＞0时，﹣3＜x＜1．
22．（2019·湖南浏阳·初三期中）已知，关于x的一元二次方程x2+(a-1)x-a=0.
(1)求证：方程总有两个实数根；
(2)若该方程有一个根是负数，求a的取值范围.
【答案】(1)证明见解析；(2)a>0.
【解析】(1)证明：∵x2+(a-1)x-a=0.∴△=（a－1）2＋4a=a2+2a＋1=（a+1）2＞0 ，∴方程总有两个实数根.
(2)由求根公式得，x=－（a－1）±（a－1）2＋4a2=－（a－1）±（a＋1）2，∴x1=1，x2=-a，∵方程有一个根是负数，∴－a＜0，∴a＞0；故答案为a＞0.
23．（2020·全国初三课时练习）如图，点O是等边三角形ABC内的一点，∠BOC＝150°，将△BOC绕点C按顺时针旋转得到△ADC，连接OD，OA．
（1）求∠ODC的度数；
（2）若OB＝2，OC＝3，求AO的长．

【答案】（1）60°；（2）
【解析】（1）由旋转的性质得：CD=CO，∠ACD=∠BCO．
∵∠ACB=60°，∴∠DCO=60°，∴△OCD为等边三角形，∴∠ODC=60°；
（2）由旋转的性质得：AD=OB=2．
∵△OCD为等边三角形，∴OD=OC=3．
∵∠BOC=150°，∠ODC=60°，∴∠ADO=90°．
在Rt△AOD中，由勾股定理得：AO．
24．（2019·河北路北·）“绿水青山就是金山银山”的理念已融入人们的日常生活中，因此，越来越多的人喜欢骑自行车出行．某自行车店在销售某型号自行车时，以高出进价的50%标价．已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同．
（1）求该型号自行车的进价和标价分别是多少元？
（2）若该型号自行车的进价不变，按（1）中的标价出售，该店平均每月可售出51辆；若每辆自行车每降价20元，每月可多售出3辆，求该型号自行车降价多少元时，每月获利最大？最大利润是多少？
【答案】（1）进价为1000元，标价为1500元；（2）该型号自行车降价80元出售每月获利最大，最大利润是26460元．
【解析】解：（1）设进价为x元，则标价是1.5x元，由题意得：
1.5x×0.9×8-8x=（1.5x-100）×7-7x，
解得：x=1000，
1.5×1000=1500（元），
答：进价为1000元，标价为1500元；
（2）设该型号自行车降价a元，利润为w元，由题意得：
w=（51+×3）（1500-1000-a），
=-（a-80）2+26460，
∵-＜0，
∴当a=80时，w最大=26460，
答：该型号自行车降价80元出售每月获利最大，最大利润是26460元．
25．（2019·河北路北·）如图是集体跳绳的示意图，绳子在最高处和最低处时可以近似看作两条对称的抛物线，分别记为C1和C2，绳子在最低点处时触地部分线段CD＝2米，两位甩绳同学的距离AB＝8米，甩绳的手最低点离地面高度AE＝BN＝ 米，最高点离地AF＝BM＝米，以地面AB、抛物线对称轴GH所在直线为x轴和y轴建立平面直角坐标系．
（1）求抛物线C1和C2的解析式；
（2）若小明离甩绳同学点A距离1米起跳，至少要跳多少米以上才能使脚不被绳子绊住？
（3）若集体跳绳每相邻两人（看成两个点）之间最小距离为0.8米，腾空后的人的最高点头顶与最低点脚底之距为1.5米，请通过计算说明，同时进行跳绳的人数最多可以容纳几人？（温馨提醒：所有同学起跳处均在直线CD上，不考虑错时跳起问题，即身体部分均在C1和C2之间才算通过），（参考数据： ＝1.414，≈1.732）

【答案】(1) ;(2) 至少要跳米以上才能使脚不被绳子绊住;(3) 8人．
【解析】解：（1）由已知得：C（﹣1，0），D（1，0），E（﹣4，），F（﹣4，），
设C2解析式为：，把代入得15a＝，
∴，
∴．
由对称性，设C1解析式，把F（﹣4，）代入得c＝，
∴
故答案为抛物线C1和C2的解析式分别为：，．
（2）把x＝﹣3代入得，
∴至少要跳米以上才能使脚不被绳子绊住．
（3）由y1﹣y2＝1.5得：
∴，
∴x1﹣x2＝≈4×1.414＝5.656，
设同时进行跳绳的人数最多可以容纳x人
则0.8（x﹣1）≤5.656，
∴x≤8.07
∴同时进行跳绳的人数最多可以容纳8人．
26．（2019·河北路北·）如图，平面直角坐标系xOy中点A的坐标为（﹣1，1），点B的坐标为（3，3），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点E．
（1）求点E的坐标；
（2）求抛物线的函数解析式；
（3）点F为线段OB上的一个动点（不与点O、B重合），直线EF与抛物线交于M、N两点（点N在y轴右侧），连接ON、BN，当四边形ABNO的面积最大时，求点N的坐标并求出四边形ABNO面积的最大值．

【答案】（1）E点坐标为(0, )；（2） ；（3）四边形ABNO面积的最大值为，此时N点坐标为(， )．
【解析】（1）设直线AB的解析式为y=mx+n，
把A（-1，1），B（3，3）代入得，解得，
所以直线AB的解析式为y＝x+，
当x=0时，y＝×0+＝，
所以E点坐标为(0，)；
（2）设抛物线解析式为y=ax2+bx+c，
把A（-1，1），B（3，3），O（0，0）代入得，解得，
所以抛物线解析式为y＝x2−x；
（3）如图，作NG∥y轴交OB于G，OB的解析式为y=x，

设N(m，m2−m)(0＜m＜3)，则G（m，m），
GN＝m−(m2−m)＝−m2+m，
S△AOB=S△AOE+S△BOE=××1+××3=3，
S△BON＝S△ONG+SBNG＝•3•(−m2+m)＝−m2+m
所以S四边形ABNO＝S△BON+S△AOB＝−m2+m+3＝− (m−)2+
当m＝时，四边形ABNO面积的最大值，最大值为，此时N点坐标为(，)．