山东省淄博市高青县（五四制）2021-2022学年九年级上学期期末考试数学试题(word版含答案)

2021—2022学年度第一学期期末复习训练题

九年级数学

一、选择题（本题有12小题，每小题5分，共60分，每小题只有一个选项是正确的，不选、多选、错选，均不得分）

1．若点A（-5，y1），B（1，y2），C（5，y3）都在反比例函数y=的图象上，则y1，y2，y3的大小关系是

A． y1＜y2＜y3  B．y1＜y3＜y2   C．y2＜y3＜y1   D．y3＜y1＜y2

2．如图是一个“凹”字形几何体，下列关于该几何体的俯视图画法正确的是

A．  B．  C．  D．

3．在直角△ABC中，∠C=90°，sinA=，那么tanB=

A．   B．   C．   D．

4．在四张完全相同的卡片上，分别画有等腰三角形、平行四边形、矩形、圆，现从中随机抽取一张，卡片上的图形既是轴对称图形又是中心对称图形的概率是

A．   B．   C．   D．1

5． 如图，△ABC内接于⊙O，若∠A=45°，OC=2，则BC的长为

A．   B．4   C．2   D．2

6．关于x的二次函数y=（m-2）x2-2x+1与x轴有两个不同的交点，则m的取值范围是

A．m≤3   B．m≤3且m≠2   C．m＜3   D．m＜3且m≠2

7．在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标（0，2），顶点B恰好落在第一象限的双曲线上，则该反比例函数的解析式为

A．y＝   B．y＝−   C．y＝   D．y＝−

8．如图，四边形ABCD内接于⊙O，连接BD．若＝，∠BDC=50°，则∠ADC的度数是

A．125°   B．130°   C．135°   D．140°

9．国家电网近来实施了新一轮农村电网改造升级工程，解决了农村供电“最后1公里”问题，电力公司在改造时把某一输电线铁塔建在了一个坡度为1：0.75的山坡CD的平台BC上（如图），测得∠AED=52.5°，BC=5米，CD=35米，DE=19米，则铁塔AB的高度约为（参考数据：sin52.5°≈0.79，cos52.5°≈0.61，tan52.5°≈1.30）

A．7.6米   B．27.5米   C．30.5米   D．58.5米

10．如图，△OAC按顺时针方向旋转，点O在坐标原点上，OA边在x轴上，OA=8，AC=4，把△OAC绕点A按顺时针方向转到△O′AC′，使得点O′的坐标是（4，4）则在这次旋转过程中线段OC扫过部分（阴影部分）的面积为

A．8π   B．   C．2π   D．48π

  第8题图             第9题图              第10题图                  第11题图

11．如图，在平面直角坐标系中，反比例函数y=（x＞0）的图象与边长是6的正方形OABC的两边AB，BC分别相交于M，N 两点．△OMN的面积为10．若动点P在x轴上，则PM+PN的最小值是

A．6   B．10   C．2   D．2

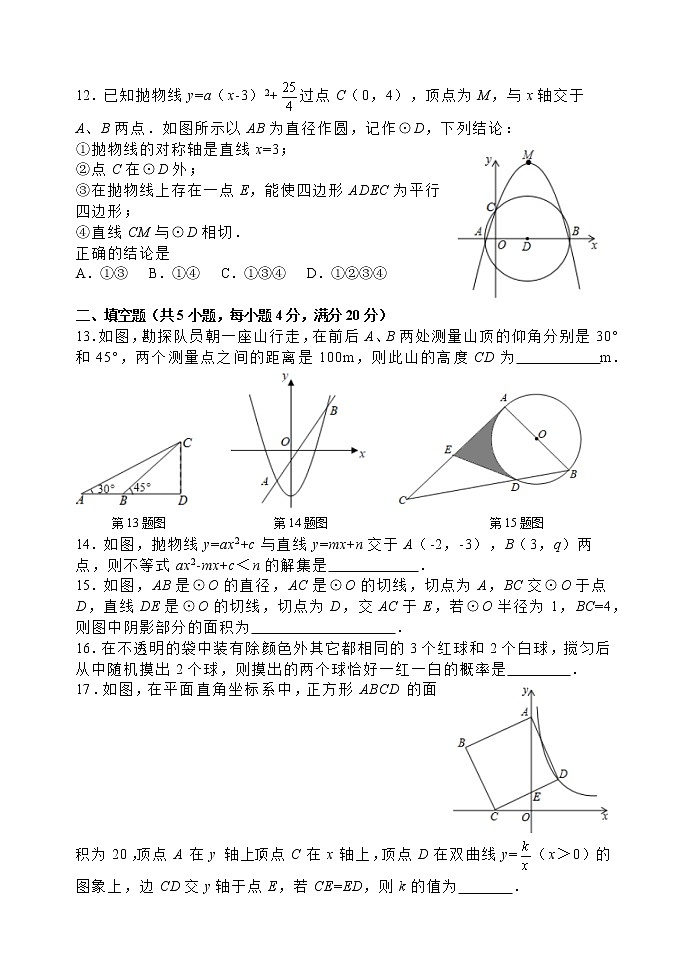
12．已知抛物线y=a（x-3）2+过点C（0，4），顶点为M，与x轴交于A、B两点．如图所示以AB为直径作圆，记作⊙D，下列结论：

①抛物线的对称轴是直线x=3；

②点C在⊙D外；

③在抛物线上存在一点E，能使四边形ADEC为平行四边形；

④直线CM与⊙D相切．

正确的结论是

A．①③   B．①④   C．①③④   D．①②③④

二、填空题（共5小题，每小题4分，满分20分）

13．如图，勘探队员朝一座山行走，在前后A、B两处测量山顶的仰角分别是30°和45°，两个测量点之间的距离是100m，则此山的高度CD为         m．

第13题图                  第14题图                           第15题图

14．如图，抛物线y=ax2+c与直线y=mx+n交于A（-2，-3），B（3，q）两点，则不等式ax2-mx+c＜n的解集是          ．

15．如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，直线DE是⊙O的切线，切点为D，交AC于E，若⊙O半径为1，BC=4，则图中阴影部分的面积为                ．

16．在不透明的袋中装有除颜色外其它都相同的3个红球和2个白球，搅匀后从中随机摸出2个球，则摸出的两个球恰好一红一白的概率是       ．

17．如图，在平面直角坐标系中，正方形ABCD的面积为20，顶点A在y轴上，顶点C在x轴上，顶点D在双曲线y=（x＞0）的图象上，边CD交y轴于点E，若CE=ED，则k的值为      ．

三、解答题（共7小题，共70分）

18．已知二次函数y=ax2+bx+3的图象经过点（-3，0），（2，-5）．

（1）试确定此二次函数的解析式；

（2）请你判断点P（-2，3）是否在这个二次函数的图象上？

19．在一只不透明的口袋里，装有若干个除了颜色外均相同的小球，某数学学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．如下表是活动进行中的一组统计数据：

（1）上表中的a=     ，b=      ；

（2）“摸到白球的”的概率的估计值是      （精确到0.1）；

（3）如果袋中有12个白球，那么袋中除了白球外，还有多少个其它颜色的球？

20．学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数与碟子的高度的关系如下表：

（1）当桌子上放有x个碟子时，请写出此时碟子的高度（用含x的式子表示）；

（2）分别从三个方向上看若干碟子，得到的三视图如上右图所示，厨房师傅想把它们整齐地叠成一摞，求叠成一摞后的高度．

21．如图，已知EF过圆O的圆心O，且弦AB⊥EF，连接AE交⊙O于点C，连接BC交EF于点D，连接OB、OC．

（1）若∠E=24°，求∠BOC的度数；

（2）若OB=2，OD=1，求DE的长．

22．如图，某校一幢教学大楼的顶部竖有一块“传承文明，启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°，然后沿山坡向上走到B处测得宣传牌顶部C的仰角为45°．已知山坡AB的坡度i=1：，（斜坡的铅直高度与水平宽度的比），经过测量AB=10米，AE=15米．

（1）求点B到地面的距离；

（2）求这块宣传牌CD的高度．（测角器的高度忽略不计，结果保留根号）

23．如图，直线y=2x+6与反比例函数y=（k＞0）的图象交于点A（m，8），与x轴交于点B，平行于x轴的直线y=n（0＜n＜6）交反比例函数的图象于点M，交AB于点N，连接BM．

（1）求m的值和反比例函数的解析式；

（2）观察图象，直接写出当x＞0时不等式2x+6-＞0的解集；

（3）直线y=n沿y轴方向平移，当n为何值时，△BMN的面积最大？最大值是多少？

24．综合与探究：

如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于C点，OA=2，OC=6，连接AC和BC．

（1）求抛物线的解析式；

（2）点E是第四象限内抛物线上的动点，连接CE和BE．求△BCE面积的最大值及此时点E的坐标；

（3）若点M是y轴上的动点，在坐标平面内是否存在点N，使以点A、C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

2021—2022学年度第一学期期末复习训练题

九年级数学参考答案

一、选择题：本题共12小题，每小题5分，共60分

二、填空题：每小题4分，共20分

三、解答题：

18．解：（1）由题意得，，解得，，

则二次函数的解析式为y=-x2-2x+3；......................................4分

（2）当x=-2时，y=-（-2）2-2×（-2）+3=3，

∴点P（-2，3）在这个二次函数的图象上．................................8分

19．解：（1）a=59÷100=0.59，b=200×0.58=116．...........................4分

（2）“摸到白球的”的概率的估计值是0.6；................................6分

（3）12÷0.6-12=8（个）．

答：除白球外，还有大约8个其它颜色的小球．.............................8分

20．解：（1）由题意得：2+1.5（x-1）=1.5x+0.5；..........................5分

（2）由三视图可知共有15个碟子，∴叠成一摞的高度=1.5×15+0.5=23（cm），

答：叠成一摞后的高度为23cm．.......................................10分

21．解：（1）∵EF⊥AB，∴∠A+∠E=90°，

∵∠E=24°，∴∠A=90°-∠E=66°，∴∠BOC=2∠A=132°；.....................5分

（2）∵OB=OC，∴∠OCB=∠OBC，

在△OBC中，∠COB=＝90°−∠BOC，

∵∠E=90°-∠A，∠A=∠BOC，∴∠OCB=∠E，

∵∠COD=∠EOC，∴△COD∽△EOC，∴，

∵OB=2，OD=1，∴，解得OE=4，

∴DE=OE-OD=3．..................................................10分

22．解：（1）过B作BF⊥AE，交EA的延长线于F，作BG⊥DE于G．

Rt△ABF中，i=tan∠BAF=，∴∠BAF=30°，

∴BF=AB=5m，AF=5m，

答：点B到地面的距离为5m；..........................................5分

（2）由（1）得：BG=AF+AE=（5+15）m．

Rt△BGC中，∠CBG=45°，∴CG=BG=（5+15）m，

Rt△ADE中，∠DAE=60°，AE=15m，∴DE=AE=15m，

∴CD=CG+GE-DE=5+15+5-15=（20-10）m．

答：宣传牌CD高为（20-10）米．......................................10分

23．解：（1）∵直线y=2x+6经过点A（1，m），

∴m=2×1+6=8，∴A（1，8），

∵反比例函数经过点A（1，8），∴k=8，

∴反比例函数的解析式为y=．..........................................4分

（2）不等式2x+6-＞0的解集为x＞1．....................................8分

（3）由题意，点M，N的坐标为M（，n），N（，n），

∵0＜n＜6，∴＜0，∴-＞0

∴S△BMN=|MN|×|yM|=×（-）×n=-（n-3）2+，

∴n=3时，△BMN的面积最大，最大值为．...............................12分

24．解：（1）∵OA=2，OC=6，∴A（-2，0），C（0，-6），

将A（-2，0），C（0，-6），代入y=x2+bx+c，

得，解得：b=-1，c=-6，

∴抛物线得解析式为：y=x2-x-6．.......................................4分

（2）在函数y=x2-x-6中，令y=0得：

    x2-x-6=0，

解得：x1=-2，x2=3，

∴B（3，0）．

如图1，连接OE，BE．

设点E（m，m2-m-6），S△BCE=S△OCE+S△OBE-S△OBC

=×6m+×3（-m2+m+6）-×3×6=−m2+m

=− (m−)2+，

根据二次函数的图象及性质可知，当m＝时，△BCE的面积有最大值，

此时点E的坐标为(，−)．..............................................8分

（3）存在；点N坐标为(−2，2)，(−2，−2)，（2，0），(−2，−)．

∵A（-2，0），C（0，-6），∴AC=＝2．

①若AC为菱形的边长，如图2，

则MN∥AC，且MN=AC=2．

N1（−2，2），N2（−2，−2），N3（2，0）．

②若AC为菱形的对角线，如图3，

则AN4∥CM4，AN4=CN4，

设N4（-2，n），则-n=，

解得：n=−．∴N4（-2，−）．

综上所述，点N坐标为(−2，2)或(−2，−2)或（2，0）或(−2，−)．...............12分