高中人教A版 (2019)3.1 函数的概念及其表示学案

【新教材】3.1.1 函数的概念（人教A版）

1.理解函数的定义、函数的定义域、值域及对应法则。

2.掌握判定函数和函数相等的方法。

3.学会求函数的定义域与函数值。

重点：函数的概念，函数的三要素。

难点：函数概念及符号y=f(x)的理解。

一、 预习导入

阅读课本60-65页，填写。

1．函数的概念

(1)函数的定义：

设A，B是           ，如果按照某种确定的对应关系f，使对于集合A中的             ，在集合B中都有        和它对应，那么就称f：A→B为从集合A到集合B的一个函数，记作              .

(2)函数的定义域与值域：

函数y＝f(x)中，x叫做      ，            叫做函数的定义域，与x的值相对应的y值叫做      ，函数值的集合          叫做函数的值域．显然，值域是集合B的      ．

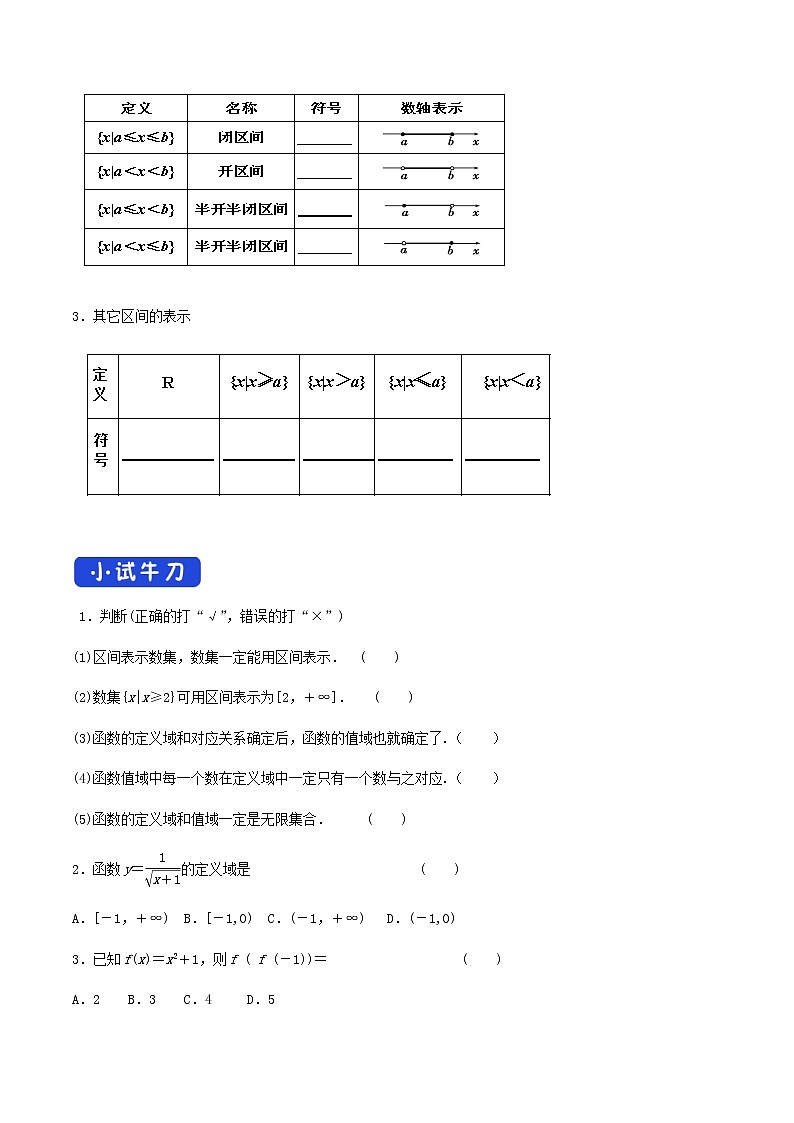
2．区间概念(a，b为实数，且a＜b)

3．其它区间的表示

1．判断(正确的打“√”，错误的打“×”)

(1)区间表示数集，数集一定能用区间表示．  (　　)

(2)数集{x|x≥2}可用区间表示为[2，＋∞]．   (　　)

(3)函数的定义域和对应关系确定后，函数的值域也就确定了.（    ）

(4)函数值域中每一个数在定义域中一定只有一个数与之对应.（    ）

(5)函数的定义域和值域一定是无限集合．     (　　)

2．函数y＝的定义域是                        (　　)

A．[－1，＋∞)  B．[－1,0)  C．(－1，＋∞)  D．(－1,0)

3．已知f(x)＝x2＋1，则f ( f (－1))＝                   (　　)

A．2　　B．3　　C．4　   D．5

4．用区间表示下列集合：

(1){x|10≤x≤100}用区间表示为________．

(2){x|x＞1}用区间表示为________．

题型一    函数的定义

例1 下列选项中(横轴表示x轴,纵轴表示y轴),表示y是x的函数的是(　　)

跟踪训练一

1.集合A={x|0≤x≤4},B={y|0≤y≤2},下列不表示从A到B的函数的是(　　)

题型二   相等函数

例2　试判断以下各组函数是否表示同一函数:

(1)f(x)=()2,g(x)=;

(2)y=x0与y=1(x≠0);

(3)y=2x+1(x∈Z)与y=2x-1(x∈Z).

跟踪训练二

1.试判断以下各组函数是否表示同一函数: ①f(x)=,g(x)=x-1;

②f(x)=,g(x)=;

③f(x)=,g(x)=x+3;

④f(x)=x+1,g(x)=x+x0;

⑤汽车匀速运动时,路程与时间的函数关系f(t)=80t(0≤t≤5)与一次函数g(x)=80x(0≤x≤5).

其中表示相等函数的是　　　　　(填上所有正确的序号). 

题型三    区间

例3 已知集合A={x|5-x≥0},集合B={x||x|-3≠0},则A∩B用区间可表示为　　　　　. 

跟踪训练三

1.集合{x|0<x<1或2≤x≤11}用区间表示为　　　　　. 

2. 若集合A=[2a-1,a+2],则实数a的取值范围用区间表示为　　　　　. 

题型四  求函数的定义域

例4 求下列函数的定义域:

(1)y=;　(2)f(x)=.

跟踪训练四

1.求函数y=的定义域.

2.已知函数f(x)的定义域是[-1,4],求函数f(2x+1)的定义域.

题型五  求函数值（域）

例5 (1)已知f(x)＝(x∈R，且x≠－1)，g(x)＝x2＋2(x∈R)，则f(2)＝________，

f(g(2))＝________.

(2)求下列函数的值域：

①y＝x＋1；     ②y＝x2－2x＋3，x∈[0,3)；

③y＝；    ④y＝2x－.

跟踪训练五

1.求下列函数的值域：

(1)y＝ ＋1；(2)y＝.

1．对于集合，，由下列图形给出的对应中，不能构成从到的函数有（　　）个

A.个 B.个 C.个 D.个

2．函数的定义域为R，则实数a的取值范围为（  ）

A．a>1 B．0<a<1 C．a<0 D．a<1

3．函数f（x）=的定义域为

A．    B．

C．    D．

4．已知函数的定义域为，则的定义域为（  ）

A. B. C. D.

5．下列各组函数中，与相等的是（   ）

A． B．

C． D．

6．集合A={x|x≤5且x≠1}用区间表示____________．

7．已知函数.

（1）求函数的定义域；

（2）求及的值．

8．求下列函数的值域：

（1）f（x）=；

（2）f（x）=x–．

答案

小试牛刀

1．（1）×  （2） ×  （3）√  （4）×  （5 ）×

2．C    

3．D

4. (1)[10,100]　(2)(1，＋∞)

自主探究

例1 【答案】D

跟踪训练一【答案】C

例2　【答案】见解析  

【解析】:(1)因为函数f(x)=()2的定义域为{x|x≥0},而g(x)=的定义域为{x|x∈R},它们的定义域不同,所以它们不表示同一函数.

(2)因为y=x0要求x≠0,且当x≠0时,y=x0=1,故y=x0与y=1(x≠0)的定义域和对应关系都相同,所以

它们表示同一函数.

(3)y=2x+1(x∈Z)与y=2x-1(x∈Z)两个函数的定义域相同,但对应关系不相同,故它们不表示同一函数.

跟踪训练二【答案】⑤

【解析】①f(x)与g(x)的定义域不同,不是同一函数;

②f(x)与g(x)的解析式不同,不是同一函数;

③f(x)=|x+3|,与g(x)的解析式不同,不是同一函数;

④f(x)与g(x)的定义域不同,不是同一函数;

⑤f(x)与g(x)的定义域、值域、对应关系皆相同,是同一函数.

例3 【答案】(-∞,-3)∪(-3,3)∪(3,5]

【解析】∵A={x|5-x≥0},∴A={x|x≤5}.

∵B={x||x|-3≠0},∴B={x|x≠±3}.

∴A∩B={x|x<-3或-3<x<3或3<x≤5},

即A∩B=(-∞,-3)∪(-3,3)∪(3,5].

跟踪训练三

【答案】(1)(0,1)∪[2,11]　(2)(-∞,3)

【解析】 (2)由区间的定义知,区间(a,b)(或[a,b])成立的条件是a<b.

∵A=[2a-1,a+2],∴2a-1<a+2.∴a<3,

∴实数a的取值范围是(-∞,3).

例4【答案】(1) (-∞,-2)∪(-2,0)　(2) (-∞,1)∪(1,4]

【解析】(1)要使函数有意义,自变量x的取值必须满足解得x<0,且x≠-2.故原函数的定义域为(-∞,-2)∪(-2,0).

(2)要使函数有意义,自变量x的取值必须满足

故原函数的定义域为(-∞,1)∪(1,4].

跟踪训练四

【答案】(1) 　(2)

【解析】(1)要使函数有意义,需

解得-≤x<2,且x≠0,所以函数y=的定义域为.

(2)已知f(x)的定义域是[-1,4],即-1≤x≤4.

故对于f(2x+1)应有-1≤2x+1≤4,

∴-2≤2x≤3,∴-1≤x≤.

∴函数f(2x+1)的定义域是.

例5

【答案】（1）  　   （2）① R  ② [2,6)  ③ {y|y∈R且y≠3}  ④   

【解析】(1)　∵f (x)＝，∴f(2)＝＝.

又∵g (x)＝x2＋2，∴g (2)＝22＋2＝6，

∴f ( g(2))＝f (6)＝＝.

(2)　①(观察法)因为x∈R，所以x＋1∈R，即函数值域是R.

②(配方法)y＝x2－2x＋3＝(x－1)2＋2，由x∈[0,3)，再结合函数的图象(如图)，可得函数的值域为[2,6)．

③(分离常数法)y＝＝＝3－.

∵≠0，∴y≠3，

∴y＝的值域为{y|y∈R且y≠3}．

④(换元法)设t＝，则t≥0且x＝t2＋1，所以y＝2(t2＋1)－t＝2 2＋，由t≥0，再结合函数的图象(如图)，可得函数的值域为.

跟踪训练五

【答案】(1) [1，＋∞)　(2)

【解析】(1)因为≥0，所以＋1≥1，即所求函数的值域为[1，＋∞)．

(2)因为y＝＝－1＋，

又函数的定义域为R，所以x2＋1≥1，所以0＜≤2，则y∈(－1,1]．

所以所求函数的值域为(－1,1].

当堂检测 

1-5．CADCD

6．

7．【答案】（1）的定义域为；（2）；

【解析】（1）依题意，，且，

故，且，即函数的定义域为.

（2），

.

8. 【答案】（1）（–∞，2）∪（2，+∞）； （2）[–，+∞）.

【解析】（1）因为f（x）==2–，所以f（x）≠2，

所以函数f（x）的值域为（–∞，2）∪（2，+∞）．

（2）令=t（t≥0），则x=t2–1，所以y=t2–t–1（t≥0）．

因为抛物线y=t2–t–1开口向上，对称轴为直线t=∈[0，+∞），

所以当t=时，y取得最小值为–，无最大值，

所以函数f（x）的值域为[–，+∞）．