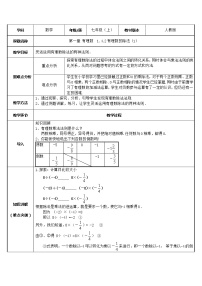
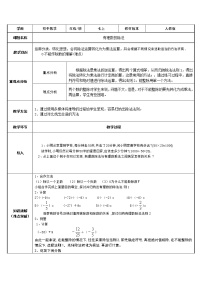
人教版七年级上册第一章 有理数1.4 有理数的乘除法1.4.2 有理数的除法第1课时教案

第一章  有理数

1.4 有理数的乘除法

1.4.2 有理数的除法

第1课时

一、教学目标

【知识与技能】

掌握有理数除法法则，会进行有理数的除法运算以及分数的化简．

【过程与方法】

通过学习有理数除法法则，体会转化思想，会将乘除混合运算统一为乘法运算．

【情感态度与价值观】

培养学生勇于探索积极思考的良好学习习惯．

二、课型

新授课

三、课时

第1课时，共2课时。

四、教学重难点

【教学重点】 

正确应用法则进行有理数的除法运算．

【教学难点】 

灵活运用有理数除法的两种法则．

五、课前准备 

教师：课件、直尺、倒数图片等。

学生：三角尺、练习本、铅笔、圆珠笔或钢笔。

六、教学过程

（一）导入新课

根据实验测定，高度每增加1km，气温大概下降6℃. 某登山运动员攀登某高峰的途中发回信息，报告他所在高度的温度是-15℃，当时地面气温为3℃. 请问你能确定登山运动员所在的位置高度吗?（出示课件2）

（二）探索新知

1.师生互动，探究有理数的除法法则（出示课件4）

教师问1：小明从家里到学校，每分钟走50米，共走了20分钟，问小明家离学校有多远？

学生回答：50×20=100.

教师问2：放学时，小明仍然以每分钟50米的速度回家，应该走多少分钟？学生回答：100 ÷50=20.

教师问3：从上面这个例子你可以发现，有理数除法与有理数乘法之间满足怎样的关系？

学生回答：有理数除法与有理数乘法互为逆运算.

教师问4：引入负数后，如何计算有理数的除法呢？ 以8÷（-4）为例．（出示课件5）

师生共同讨论后解答如下：根据除法意义，这就是要求一个数，使它与-4相乘得8．   

因为 （-2）×（-4）=8

所以 8÷（-4）=-2               ①

另外，我们知道，8×（-）=-2   ②

由①、②得 8÷（-4）=8×（-） ③

③式表明，一个数除以-4可以转化为乘以-来进行，即一个数除以-4，等于乘以-4的倒数-．

教师问5：对于其他的数是不是也可以呢？请完成下面的题目：（出示课件6）

学生回答：中间组由上到下答案依次为：-2，-6，，-8；右边组由上到下答案依次为：-2，-6，，-8；

教师问6：上面各组数计算结果有什么关系？由此你能得到有理数的除法法则了吗？
    学生回答：上面各组数计算结果相等，有理数的除法可以转化为乘法进行计算.

教师问7：观察下列两组式子，你能找到它们的共同点吗？（出示课件7）

学生回答：除以一个数等于乘以它的倒数.

教师问8：除数能为0吗？

学生回答：不能为0.

教师问9：换其他数的除法进行类似讨论，是否仍有除以a（a≠0）可以转化为乘以呢？[例如（-10）÷（-0.4）]

学生做题后回答：仍然可以.

总结点拨： 从而得出有理数除法法则：（出示课件8）

除以一个不等于0的数，等于乘以这个数的倒数．

这个法则也可以表示成：

    a÷b=a·（b≠0），

其中a、b表示任意有理数（b≠0）

教师问10：利用上面的除法法则计算下列各题.（出示课件9）

（1）(–54)÷ (–9)；            （2）(–27) ÷3；
（3）0 ÷ (–7)；                （4）(–24) ÷(–6).
学生回答：（1）6；（2）-9；（3）0；（4）4

教师问11：从上面我们能发现商的符号有什么规律？

学生回答：同号得正，异号得负.

总结点拨：（出示课件10）

两数相除，同号得正，异号得负，并把绝对值相除．

零除以任何一个不等于零的数，都得零．

教师问12：到现在为止我们有了两个除法法则，那么两个法则是不是都可以用于解决两数相除呢？（出示课件11）
    师生共同解答如下：

1. 两个法则都可以用来求两个有理数相除.
2. 如果两数相除，能够整除的就选择法则二，不能够整除的就选择用法则一.
例1：计算:（出示课件12）

（1）(–36) ÷ 9；（2）（-）÷（-） .
师生共同解答如下：

解：（1）(–36) ÷ 9= –(36× )= –4；
        （2）
    例2：化简下列各式：（出示课件14）

（1）    ；（2） .
师生共同解答如下：

解：（1）
    （2）

例3：计算：（出示课件）
    （1） （2）
    师生共同解答如下：

解：（1）原式=125 ÷5                                    
            =（125+）×                                                       
            =125×+×
            =25+
            =25
    点拨：如果有带分数，可以将带分数写成整数部分和分数部分的和，利用分配律进行运算，更加简便.

（2）原式=××

= 1

点拨：将小数化为分数.

总结点拨：1. 有理数除法化为有理数乘法以后，可以利用有理数乘法的运算律简化运算.
    2. 乘除混合运算往往先将除法化为乘法，然后确定积的符号，最后求出结果（乘除混合运算按从左到右的顺序进行计算）.
    （三）课堂练习（出示课件19-22）

1. (–21) ÷7的结果是（　 　）
     A．3      B．–3               C．           D. –
    2. 计算：(–12) ÷ 3=_______．

3. 填空：（1）若a，b互为相反数，且a ≠ b，则=________；

（2）当a < 0时，   =_______；

（3）若 a>b，<0，则a，b的符号分别是__________.
（4）若–3x=12，则x =_____.
4.若，则=_________.

5. （1）计算（-）÷（- 2） ；（2）计算-0.5÷×（-）；

（3）计算（-7）÷（-）÷（-）                            

参考答案：

1.B

2.-4

3.（1）-1；（2）-1；（3）a>0，b<0；（4）-4

4.-1 解析：由题意得，，解得x=-3，y=3,所以=-1.

5.解：（1）原式=×           
              =
  （2）原式=××             

         =
（3）原式=-7××               

         =-
（四）课堂小结

今天我们学了哪些内容:

除以一个不等于0的数，等于乘以这个数的倒数．

两数相除，同号得正，异号得负，并把绝对值相除．

零除以任何一个不等于零的数，都得零．

（五）课前预习

预习下节课（1.4.2）36页到37页的相关内容。

知道有理数加减乘除混合运算的顺序.

七、课后作业

1、教材36页练习1,2

2、计算.

(1)(-1155)÷[(-11)×(+3)×(-5)];        (2)375÷;

八、板书设计：

九、教学反思：

1.前面已学过有理数加法、减法、乘法，这些运算为学习有理数除法作了铺垫，而除法在小学时已经接触到过，学生也知道除法是乘法的逆运算．本课的重点是有理数的除法法则．通过小组讨论、小组合作，不仅能突破重点，也能培养学生观察问题、分析问题和解决问题的能力．

2.有理数除法是一种运算．在上课时，既要减少一些繁难的例题，又要通过一定的练习使学生能熟练地运用法则，进行准确的计算．

3.通过例题讲解和练习训练，使学生注意到以下两点：（1）有理数除法法则遵循“符号优先”原则，即先确定符号，再把绝对值相除．（2）对于多个有理数相除，运算时可以从左到右进行，也可把除法转化成乘法后再进行计算．

4.通过学生自主学习、探究，培养学生自立的精神．在学习中，教师可以有意识地培养学生的竞争意识，让学生在学习过程中能及时反思自己出现的问题，培养良好的学习习惯．