

高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式测试题
展开
这是一份高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式测试题,共6页。
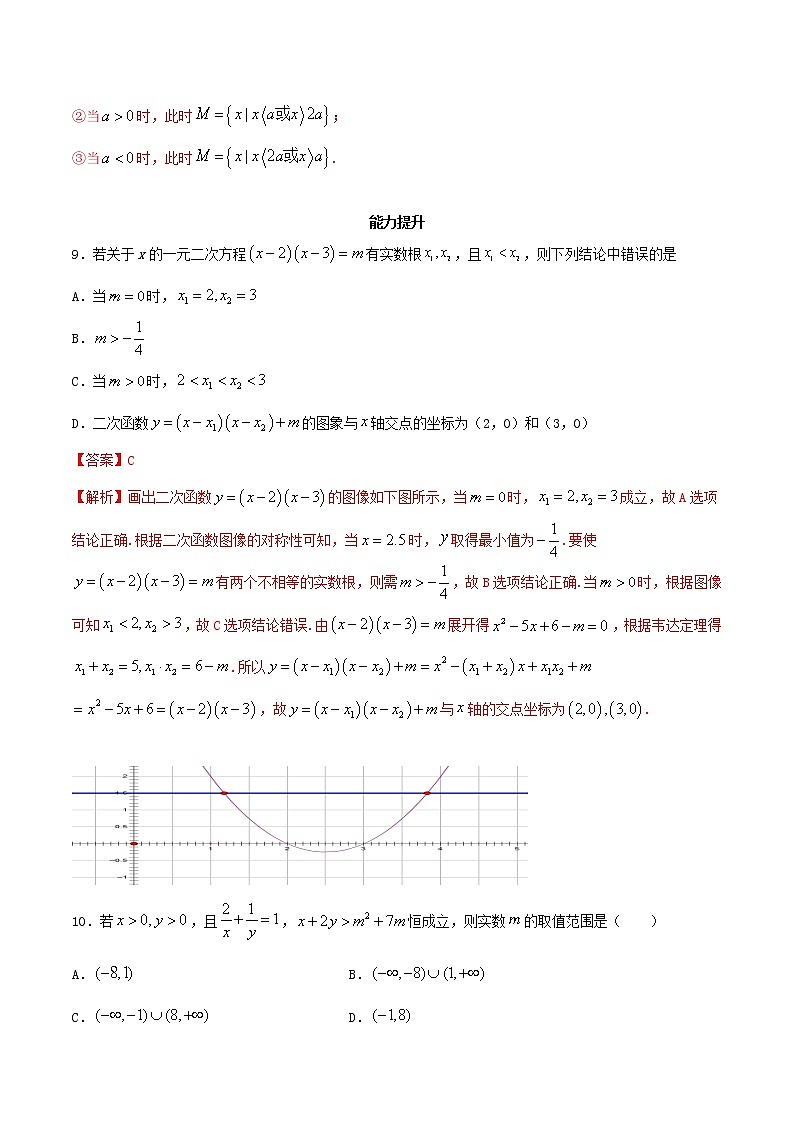
2.3二次函数与一元二次方程、不等式【本节明细表】 知识点、方法题号解不等式1,2,4,8根据解集求参3,6,7不等式恒成立问题5,9,10,11实际应用12,13基础巩固1.不等式的解集是( )A. B. C. D.或【答案】D【解析】不等式x2>1,移项得:x2﹣1>0,因式分解得:(x+1)(x﹣1)>0,则原不等式的解集为{x|x<-1或x>1}.故选:D.2.不等式的解集为( )A. B.C. D.【答案】B【解析】将不等式化为,解得,所以解集为故选B.3.若关于的不等式的解集是,则实数等于( )A.-1 B.-2 C.1 D.2【答案】C【解析】由题意不等式的解集是,所以方程的解是,则,解得,故选C.4.已知集合,,则( )A. B.或}C. D.或}【答案】C【解析】由题意可得,,所以.故选C.5.若对任意,不等式恒成立,则a的取值范围为( )A. B. C. D.【答案】D【解析】对任意,不等式恒成立即恒成立故答案为D6.已知关于的不等式的解集为,则等于________【答案】-1【解析】由题得、2为方程的根,将代入,得,即.7.若关于的不等式有解,则实数的取值范围为________.【答案】【解析】不等式有解等价于有解,所以,故或,填.8.已知关于的不等式的解集为.(1)当时,求;(2)当时,求.【答案】(1) (2)见解析【解析】(1)由题得,所以不等式的解集为,故M= .(2)①当时,此时关于的不等式为,;②当时,此时;③当时,此时. 能力提升9.若关于x的一元二次方程有实数根,且,则下列结论中错误的是A.当时,B.C.当时,D.二次函数的图象与轴交点的坐标为(2,0)和(3,0)【答案】C【解析】画出二次函数的图像如下图所示,当时,成立,故A选项结论正确.根据二次函数图像的对称性可知,当时,取得最小值为.要使有两个不相等的实数根,则需,故B选项结论正确.当时,根据图像可知,故C选项结论错误.由展开得,根据韦达定理得.所以,故与轴的交点坐标为. 10.若,且,恒成立,则实数的取值范围是( )A. B.C. D.【答案】A【解析】由基本不等式得,当且仅当,即当时,等号成立,所以,的最小值为.由题意可得,即,解得或.因此,实数的取值范围是,故选:B.11.已知函数.(1)求不等式的解集;(2)若当时,恒成立,求实数的取值范围.【答案】(1)见解析;(2) 【解析】(1)不等式可化为:,①当时,不等无解;②当时,不等式的解集为;③当时,不等式的解集为.(2)由可化为:,必有:,化为,解得:.12.某种产品的成本是120元/件,试销阶段每件产品的售价x(元)与产品的日销售量y(件)之间的关系如下表所示:x/元130150165y/件705035 若日销售量y是销售价x的一次函数,那么,要使每天所获得的利润最大,每件产品的销售价应定为多少元?此时每天的销售利润是多少?【答案】每件产品的销售价为160元,每天的销售利润为1 600元. 【解析】设,则∴∴当每件的销售价为x元时,每件的销售利润为元,每天的销售利润为S.则.∴当时,元.答:每件产品的销售价为160元,每天的销售利润为1 600元. 素养达成13.某小型机械厂有工人共名,工人年薪4万元/人,据悉该厂每年生产台机器,除工人工资外,还需投入成本为(万元),且每台机器售价为万元.通过市场分析,该厂生产的机器能全部售完.(1)写出年利润(万元)关于年产量的函数解析式;(2)问:年产量为多少台时,该厂所获利润最大?【答案】(1);(2)100台时,850万元【解析】(1)依题意有.(2)当时,此时时,取得最大值万元; 当时, 当且仅当时,即时,取得最大值万元. 综上可知当年产量为100台时,该厂在生产中获利最大,最大利润为850万元.
相关试卷
这是一份高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.3 二次函数与一元二次方程、不等式第1课时课后作业题,共6页。试卷主要包含了 解关于x的不等式, 解不等式等内容,欢迎下载使用。
这是一份高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.1 等式性质与不等式性质课堂检测,共5页。
这是一份人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式习题,共10页。









