人教A版 (2019)必修 第一册5.7 三角函数的应用巩固练习

这是一份人教A版 (2019)必修 第一册5.7 三角函数的应用巩固练习，共6页。试卷主要包含了7 三角函数的应用，5－0等内容，欢迎下载使用。
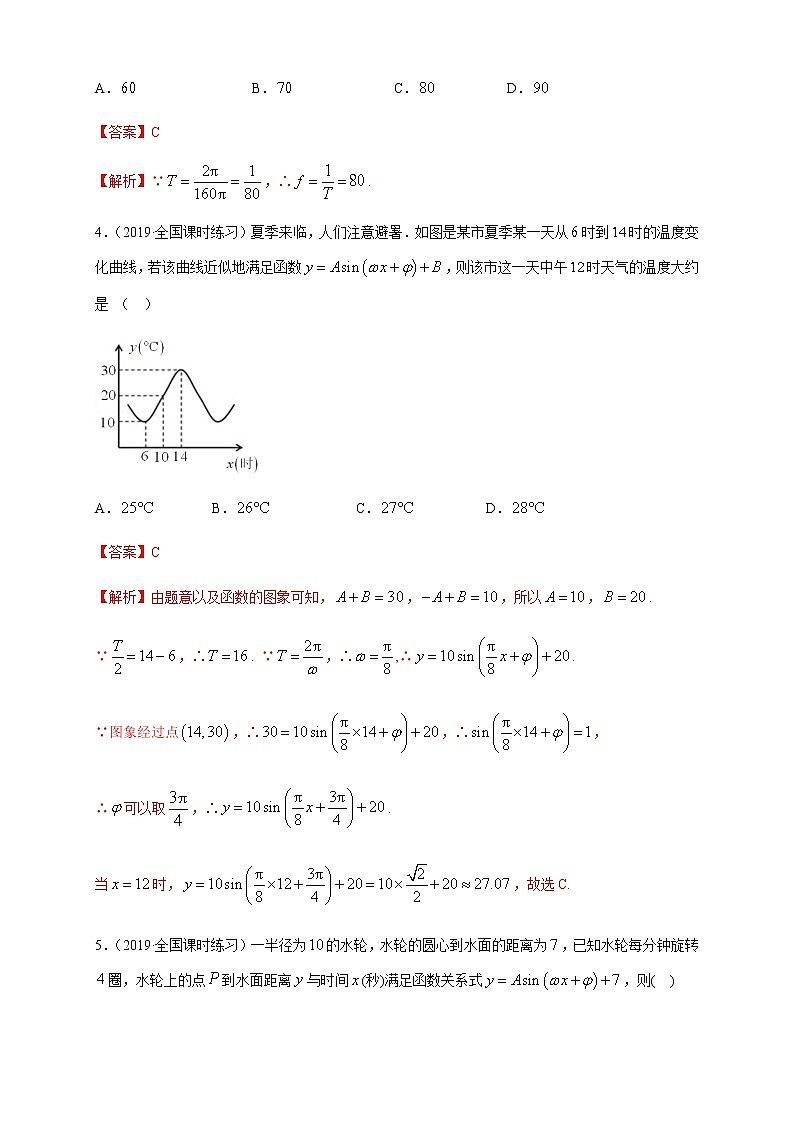
第五章  三角函数5.7  三角函数的应用一、选择题1．（2019·全国课时练习）一根长的线，一端固定，另一端悬挂一个小球，小球摆动时离开平衡位置的位移与时间的函数关系式是，其中是重力加速度，当小球摆动的周期是时，线长等于 (  )A．           B．           C．          D．【答案】D【解析】∵，∴，∴.2．（2019·全国课时练习）如图，设点A是单位圆上的一定点，动点P从A出发在圆上按逆时针方向旋转一周，点P所转过的弧AP的长为l，弦AP的长为d，则的图象大致是(    )A． B． C． D．【答案】C【解析】由题意得：.结合图象知应该选C.3．（2019·全国课时练习）某人的血压满足函数关系式，其中，为血压，为时间（单位：分钟），则此人每分钟心跳的次数是    (  )A．                B．              C．          D．【答案】C【解析】∵，∴.4．（2019·全国课时练习）夏季来临，人们注意避暑．如图是某市夏季某一天从时到时的温度变化曲线，若该曲线近似地满足函数，则该市这一天中午时天气的温度大约是 （  ）A．        B．            C．          D．【答案】C【解析】由题意以及函数的图象可知，，，所以，.∵，∴. ∵，∴,∴.∵图象经过点，∴，∴，∴可以取，∴.当时，，故选C.5．（2019·全国课时练习）一半径为的水轮，水轮的圆心到水面的距离为，已知水轮每分钟旋转圈，水轮上的点到水面距离与时间(秒)满足函数关系式，则(  )A．，                 B．，C．，                 D．，【答案】A【解析】，，.6．（2019·长沙市南雅中学高一月考）车流量被定义为单位时间内通过十字路口的车辆数，单位为 辆／分，上班高峰期某十字路口的车流量由函数F（t）=50+4sin（其中0≤t≤20）给出，F（t）的单位是辆／分，t的单位是分，则在下列哪个时间段内车流量是增加的 （ ）A．[0，5] B．[5，10] C．[10，15] D．[15，20]【答案】C【解析】函数可看成由和合而成，那么由（）得，所以函数在（）上单调递增，当时，，此时；故选C．二、填空题7．（2019·全国课时练习）电流随时间变化的关系式是，则当时，电流为          【答案】【解析】将代入得．8．（2019·全国高一课时练习）振动量y＝sin(ωx＋φ)(ω>0)的初相和频率分别是－π和，则它的相位是________．【答案】3πx－π【解析】∵f＝，∴T＝，∴ω＝＝3π，又φ＝－π，∴y＝sin(3πx－π)，∴振动量y的相位是3πx－π.9．（2019·全国高一课时练习）如图，是弹簧振子做简谐振动的图象，横轴表示振动的时间，纵轴表示振动的位移，则这个振子振动的函数解析式是________. 【答案】y＝2sin【解析】A＝2，T＝2(0.5－0.1)＝0.8，∴ω＝＝，∴y＝2sin，将(0.1,2)代入得：×0.1＋φ＝，∴φ＝，∴y＝2sin.10．（2019·全国课时练习）某时钟的秒针端点到中心的距离为，秒针匀速绕点旋转到点，当时间时，点与钟面上标的点重合，将、两点间的距离表示成的函数，则________，其中．【答案】【解析】由题意设，其中，. ∴.三、解答题11．（2019·全国课时练习）如图所示为一个观览车示意图，该观览车半径为，圆上最低点与地面距离为，秒转动一圈，图中与地面垂直，以为始边，逆时针转动角到，设点与地面距离为.(1)求与间关系的函数解析式；(2)设从开始转动，经过秒到达，求与间关系的函数解析式．【答案】(1)    (2)【解析】(1)过点作地面的平行线，过点作的垂线交于点．当时，，；当，时，上述解析式也适合．综上所述，.(2)点在上逆时针运动的角速度是，∴秒转过的弧度数为，∴．12．（2019·全国高一课时练习）某房地产开发商为吸引更多消费者购房,决定在一块闲置的扇形空地中修建一个花园.如图,已知扇形AOB的圆心角∠AOB=,半径为R.现欲修建的花园为▱OMNH,其中M,H分别在OA,OB上,N在上.设∠MON=θ,▱OMNH的面积为S.(1)将S表示为关于θ的函数;(2)求S的最大值及相应的θ值.【答案】（1）S=R2(cos θ-sin θ)sin θ,θ∈；（2）θ=时,S取得最大值R2.【解析】分析（1）分别过N，H作ND⊥OA于D，HE⊥OA于E，则HEDN为矩形，求出边长，即可求S关于θ的函数关系式；（2）利用二倍角公式、两角和的正弦函数化简函数的表达式为一个角的一个三角函数的形式，通过θ的范围求出S的最大值及相应的θ角.【详解】(1)如图,过N作NP⊥OA于点P,过H作HE⊥OA于点E,∵∠AOB=,∴OE=EH=NP=Rsin θ,OP=Rcos θ,∴HN=EP=OP-OE=R(cos θ-sin θ),∴S=HN·NP=R2(cos θ-sin θ)sin θ,θ∈.(2)S=R2(cos θsin θ-sin2θ)=R2=R2(sin 2θ+cos 2θ-1)=R2,∵θ∈,∴2θ+,∴当2θ+,即θ=时,S取得最大值,且最大值为R2.