2023中考数学一轮复习测试卷6.1《圆的基本性质》(2份打包，教师版+答案版)

这是一份2023中考数学一轮复习测试卷6.1《圆的基本性质》(2份打包，教师版+答案版)，文件包含2023中考数学一轮复习测试卷61《圆的基本性质》含答案doc、2023中考数学一轮复习测试卷61《圆的基本性质》教师版doc等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
一、选择题
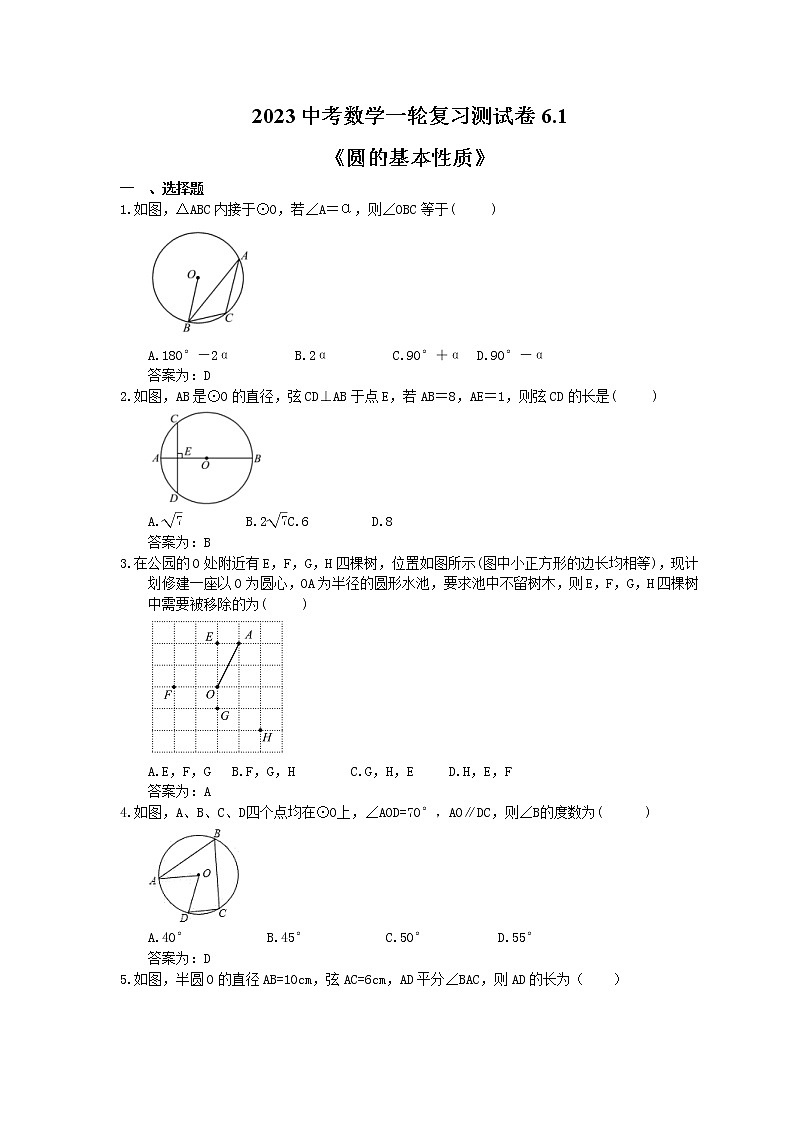
如图，△ABC内接于⊙O，若∠A＝α，则∠OBC等于( )
A.180°－2α B.2α C.90°＋α D.90°－α
答案为：D
如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB＝8，AE＝1，则弦CD的长是( )
A.eq \r(7) B.2eq \r(7)C.6 D.8
答案为：B
在公园的O处附近有E，F，G，H四棵树，位置如图所示(图中小正方形的边长均相等)，现计划修建一座以O为圆心，OA为半径的圆形水池，要求池中不留树木，则E，F，G，H四棵树中需要被移除的为( )
A.E，F，G B.F，G，H C.G，H，E D.H，E，F
答案为：A
如图，A、B、C、D四个点均在⊙O上，∠AOD=70°，AO∥DC，则∠B的度数为( )
A.40° B.45° C.50° D.55°
答案为：D
如图，半圆O的直径AB=10cm，弦AC=6cm，AD平分∠BAC，则AD的长为（ ）
A. cm B. cm C. cm D.4cm
A
如图，△ABC内接于⊙O，∠OBC=40°，则∠A的度数为( )

A．80° B．100° C．110° D．130°
D
如图，AB是半圆O的直径，C是半圆O上一点，CD是⊙O的切线，OD∥BC，OD与半圆O交于点E，则下列结论中不一定正确的是( )
A.AC⊥BC B.BE平分∠ABC C.BE∥CD D.∠D=∠A
答案为：C.
如图，点C是以点O为圆心，AB为直径的半圆上的动点(点C不与点A，B重合)，AB=4.设弦AC的长为x，△ABC的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是( )
A.B.C.D.
答案为：B.
在一次数学课上，老师出示了一道题目：
如图，CB是⊙O的弦，点A是优弧上的一动点，且AD⊥BC于点D，AF是⊙O的直径，请写出三个一定正确的结论．小明思考后，写出了三个结论：
①∠BAD=∠CAF；②AD=BD；③AB•AC=AD•AF.你认为小明写正确的有（ ）

A.0个 B.1个 C.2个 D.3个
C
如图，在矩形ABCD中，AB=4，BC=6，E是矩形内部的一个动点，且AE⊥BE，则线段CE的最小值为（ ）

A.1.5 B.2﹣2 C.2﹣2 D.4
B．
二、填空题
如图，已知在△ABC中，AB＝AC.以AB为直径作半圆O，交BC于点D.若∠BAC＝40°，则eq \(AD,\s\up8(︵))的度数是________度.
答案为：140
如图，点P是四边形ABCD外接圆⊙O上任意一点，且不与四边形顶点重合，AD是⊙O的直径，AB＝BC＝CD，连结PA，PB，PC.若PA＝a，则点A到PB和PC的距离之和AE＋AF＝__________.
答案为：eq \f(1＋\r(3),2)a
在平面直角坐标系中，以原点O为圆心的圆过点A(13，0)，直线y＝kx－3k＋4与⊙O交于B，C两点，则弦BC的长的最小值为________.
答案为：24
小明发现相机快门打开过程中，光圈大小变化如图1所示，于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形，若PQ所在的直线经过点M，PB＝5 cm，小正六边形的面积为eq \f(49\r(3),2) cm2，则该圆的半径为______cm.
答案为：8
三、解答题
如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，∠1＝∠BCD.
(1)求证：CB∥PD；
(2)若BC＝3，sin ∠BPD＝eq \f(3,5)，求⊙O的直径.
(1)证明：∵∠D＝∠1，∠1＝∠BCD，
∴∠D＝∠BCD，∴CB∥PD.
(2)解：如图，连结AC.
∵AB是⊙O的直径，∴∠ACB＝90°.
∵CD⊥AB，∴eq \(CB,\s\up8(︵))＝eq \(BD,\s\up8(︵))，
∴∠BPD＝∠CAB，
∴sin∠CAB＝sin∠BPD＝eq \f(3,5)，即eq \f(BC,AB)＝eq \f(3,5).
∵BC＝3，
∴AB＝5，即⊙O的直径是5.
如图，AB是⊙O的直径，弦CD交AB于点E，OF⊥AC于点F.
(1)请探索OF和BC的关系并说明理由；
(2)若∠D＝30°，BC＝1时，求圆中阴影部分的面积(结果保留π).
解：(1)OF∥BC，OF＝eq \f(1,2)BC.理由如下：
由垂径定理得AF＝CF.
∵AO＝BO，
∴OF是△ABC的中位线.
∴OF∥BC，OF＝eq \f(1,2)BC.
(2)连结OC.由(1)知OF＝eq \f(1,2)BC.
∵AB是⊙O的直径，∴∠ACB＝90°.
∵∠D＝30°，∴∠A＝30°.
∴AB＝2BC＝2，∴AC＝eq \r(3).
∴S△AOC＝eq \f(1,2)×AC×OF＝eq \f(\r(3),4).
易得∠AOC＝120°，OA＝1，
∴S扇形AOC＝eq \f(120·π·OA2,360)＝eq \f(π,3).
∴S阴影＝S扇形AOC－S△AOC＝eq \f(π,3)－eq \f(\r(3),4).
四、综合题
如图1，直线l：y＝－eq \f(3,4)x＋b与x轴交于点A(4，0)，与y轴交于点B，点C是线段OA上一动点(0＜AC＜eq \f(16,5)).以点A为圆心，AC长为半径作⊙A交x轴于另一点D，交线段AB于点E，连结OE并延长交⊙A于点F.
(1)求直线l的函数表达式和tan∠BAO的值；
(2)如图2，连结CE，当CE＝EF时，
①求证：△OCE∽△OEA；
②求点E的坐标；
(3)当点C在线段OA上运动时，求OE·EF的最大值.
(1)解：∵直线l：y＝－eq \f(3,4)x＋b与x轴交于点A(4，0)，
∴－eq \f(3,4)×4＋b＝0，∴b＝3，
∴直线l的函数表达式y＝－eq \f(3,4)x＋3，
∴B(0，3)，∴OA＝4，OB＝3.
在Rt△AOB中，tan∠BAO＝eq \f(OB,OA)＝eq \f(3,4).
(2)①证明：如图，连结DF，DE.
∵CE＝EF，
∴∠CDE＝∠FDE，∴∠CDF＝2∠CDE.
∵∠OAE＝2∠CDE，∴∠OAE＝∠ODF.
∵四边形CEFD是⊙O的圆内接四边形，
∴∠OEC＝∠ODF，∴∠OEC＝∠OAE.
∵∠COE＝∠EOA，∴△COE∽△EOA.
②解：如图，过点E作EM⊥OA于M.
由①知，tan∠OAB＝eq \f(3,4).
设EM＝3m，则AM＝4m，
∴OM＝4－4m，AE＝5m，
∴E(4－4m，3m)，AC＝5m，
∴OC＝4－5m.
由①知，△COE∽△EOA，
∴eq \f(OC,OE)＝eq \f(OE,OA)，
∴OE2＝OA·OC＝4(4－5m)＝16－20m.
∵E(4－4m，3m)，∴(4－4m)2＋9m2＝25m2－32m＋16，
∴25m2－32m＋16＝16－20m，
∴m＝0(舍去)或m＝eq \f(12,25)，
∴4－4m＝eq \f(52,25)，3m＝eq \f(36,25)，
∴E(eq \f(52,25)，eq \f(36,25)).
(3)解：如图，设⊙O的半径为r，过点O作OG⊥AB于G，连结FH.
∵A(4，0)，B(0，3)，
∴OA＝4，OB＝3，∴AB＝5，
∴eq \f(1,2)AB×OG＝eq \f(1,2)OA×OB，∴OG＝eq \f(12,5)，
∴AG＝eq \f(OG,tan ∠AOB)＝eq \f(12,5)×eq \f(4,3)＝eq \f(16,5)，
∴EG＝AG－AE＝eq \f(16,5)－r.
∵EH是⊙O直径，∴EH＝2r，∠EFH＝90°＝∠EGO.
∵∠OEG＝∠HEF，
∴△OEG∽△HEF，∴eq \f(OE,HE)＝eq \f(EG,EF)，
∴OE·EF＝HE·EG＝2r(eq \f(16,5)－r)＝－2(r－eq \f(8,5))2＋eq \f(128,25)，
∴当r＝eq \f(8,5)时，OE·EF最大值为eq \f(128,25).
如图，已知线段AB＝2，MN⊥AB于点M，且AM＝BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C(点C在线段BD上)，连结AC，DE.
(1)当∠APB＝30°时，求∠B的度数；
(2)求证：AB2＝BC·PB；
(3)在点P的运动过程中，当MP＝4时，取四边形ACDE一边的两端点和线段MP上一点Q，若以这三点为顶点的三角形是直角三角形，且Q为锐角顶点，求所有满足条件的MQ的值.
(1)解：∵MN⊥AB，AM＝BM，
∴PA＝PB，∴∠PAB＝∠B.
∵∠APB＝30°，∴∠B＝75°.
(2)证明：如图1，连结MD.
图1
∵MD为△PAB的中位线，
∴MD∥AP，∴∠MDB＝∠APB.
∵∠BAC＝∠MDC＝∠APB，
又∵∠BAP＝180°－∠APB－∠B，∠ACB＝180°－∠BAC－∠B，
∴∠BAP＝∠ACB.
∵∠BAP＝∠B，∴∠ACB＝∠B，
∴AC＝AB，由(1)可知PA＝PB，
∴△ABC∽△PBA，∴eq \f(AB,PB)＝eq \f(BC,AB)，
∴AB2＝BC·PB.
(3)解：如图2，记MP与圆的另一个交点为R.
图2
∵MD是Rt△MBP的中线，∴DM＝DP，
∴∠DPM＝∠DMP＝∠RCD，
∴RC＝RP.
∵∠ACR＝∠AMR＝90°，
∴AM2＋MR2＝AR2＝AC2＋CR2，
∴12＋MR2＝22＋PR2，
∴12＋(4－PR)2＝22＋PR2，
∴PR＝eq \f(13,8)，∴MR＝eq \f(19,8).
Ⅰ.当∠ACQ＝90°时，AQ为圆的直径，
∴Q与R重合，∴MQ＝MR＝eq \f(19,8)；
Ⅱ.如图3，当∠QCD＝90°时，
图3
在Rt△QCP中，PQ＝2PR＝eq \f(13,4)，
∴MQ＝eq \f(3,4)；
Ⅲ.如图4，当∠QDC＝90°时，
图4
∵BM＝1，MP＝4，∴BP＝eq \r(17)，
∴DP＝eq \f(1,2)BP＝eq \f(\r(17),2).
∵cs∠MPB＝eq \f(MP,PB)＝eq \f(DP,PQ)，∴PQ＝eq \f(17,8)，
∴MQ＝eq \f(15,8).
Ⅳ.如图5，当∠AEQ＝90°时，
图5
由对称性可得∠AEQ＝∠BDQ＝90°，
∴MQ＝eq \f(15,8).
综上所述，MQ的值为eq \f(19,8)或eq \f(3,4)或eq \f(15,8).