山东省济宁市三年（2020-2022）中考数学真题分类汇编-选择题

这是一份山东省济宁市三年（2020-2022）中考数学真题分类汇编-选择题，共23页。
山东省济宁市三年（2020-2022）中考数学真题分类汇编-选择题
一．正数和负数（共1小题）
1．（2021•济宁）若盈余2万元记作+2万元，则﹣2万元表示（　　）
A．盈余2万元 B．亏损2万元
C．亏损﹣2万元 D．不盈余也不亏损
二．相反数（共1小题）
2．（2020•济宁）﹣的相反数是（　　）
A．﹣ B．﹣ C． D．
三．近似数和有效数字（共2小题）
3．（2022•济宁）用四舍五入法取近似值，将数0.0158精确到0.001的结果是（　　）
A．0.015 B．0.016 C．0.01 D．0.02
4．（2020•济宁）用四舍五入法将数3.14159精确到千分位的结果是（　　）
A．3.1 B．3.14 C．3.142 D．3.141
四．规律型：数字的变化类（共1小题）
5．（2021•济宁）按规律排列的一组数据：，，□，，，，…，其中□内应填的数是（　　）
A． B． C． D．
五．规律型：图形的变化类（共1小题）
6．（2022•济宁）如图，用相同的圆点按照一定的规律拼出图形．第一幅图4个圆点，第二幅图7个圆点，第三幅图10个圆点，第四幅图13个圆点……按照此规律，第一百幅图中圆点的个数是（　　）

A．297 B．301 C．303 D．400
六．同底数幂的除法（共1小题）
7．（2021•济宁）下列各式中，正确的是（　　）
A．x+2x＝3x2 B．﹣（x﹣y）＝﹣x﹣y
C．（x2）3＝x5 D．x5÷x3＝x2
七．因式分解的意义（共1小题）
8．（2022•济宁）下面各式从左到右的变形，属于因式分解的是（　　）
A．x2﹣x﹣1＝x（x﹣1）﹣1 B．x2﹣1＝（x﹣1）2
C．x2﹣x﹣6＝（x﹣3）（x+2） D．x（x﹣1）＝x2﹣x
八．分式的混合运算（共1小题）
9．（2021•济宁）计算÷（a+1﹣）的结果是（　　）
A． B．
C． D．
九．零指数幂（共1小题）
10．（2022•济宁）下列各式运算正确的是（　　）
A．﹣3（x﹣y）＝﹣3x+y B．x3•x2＝x6
C．（π﹣3.14）0＝1 D．（x3）2＝x5
一十．最简二次根式（共1小题）
11．（2020•济宁）下列各式是最简二次根式的是（　　）
A． B． C． D．
一十一．根与系数的关系（共1小题）
12．（2021•济宁）已知m，n是一元二次方程x2+x﹣2021＝0的两个实数根，则代数式m2+2m+n的值等于（　　）
A．2019 B．2020 C．2021 D．2022
一十二．由实际问题抽象出分式方程（共1小题）
13．（2022•济宁）一辆汽车开往距出发地420km的目的地，若这辆汽车比原计划每小时多行10km，则提前1小时到达目的地．设这辆汽车原计划的速度是xkm/h，根据题意所列方程是（　　）
A．＝+1 B．+1＝
C．＝+1 D．+1＝
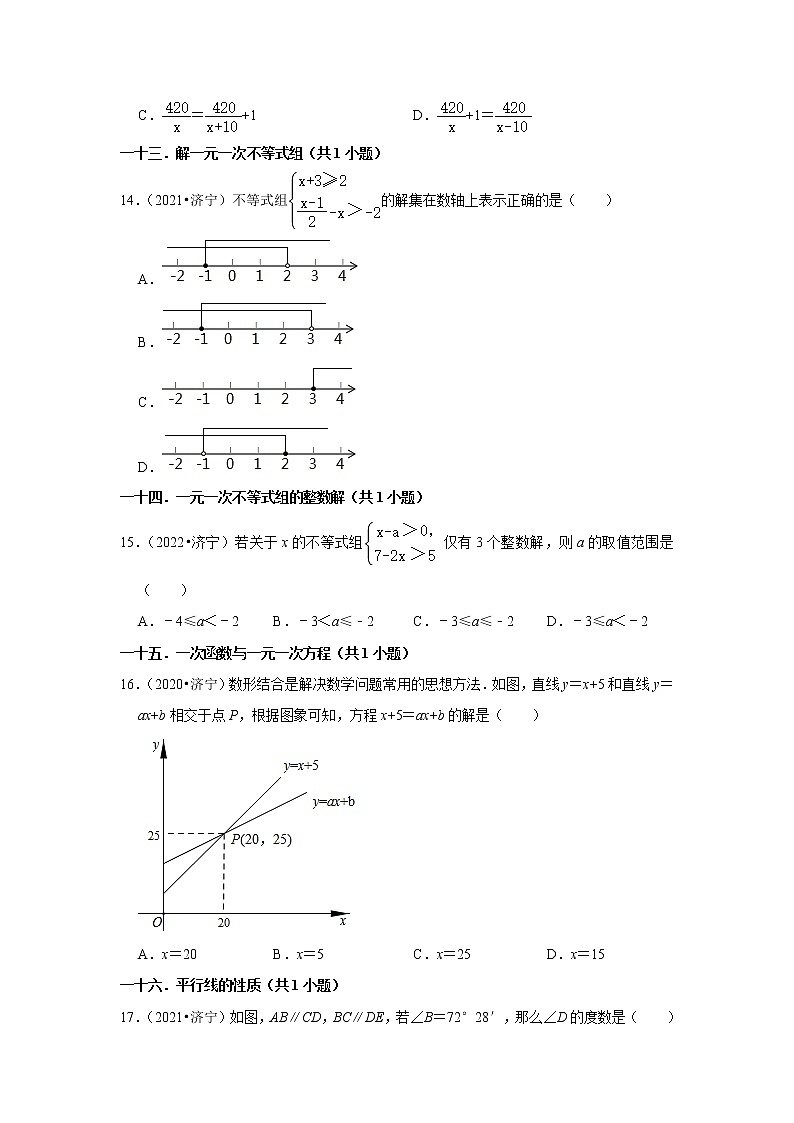
一十三．解一元一次不等式组（共1小题）
14．（2021•济宁）不等式组的解集在数轴上表示正确的是（　　）
A．
B．
C．
D．
一十四．一元一次不等式组的整数解（共1小题）
15．（2022•济宁）若关于x的不等式组仅有3个整数解，则a的取值范围是（　　）
A．﹣4≤a＜﹣2 B．﹣3＜a≤﹣2 C．﹣3≤a≤﹣2 D．﹣3≤a＜﹣2
一十五．一次函数与一元一次方程（共1小题）
16．（2020•济宁）数形结合是解决数学问题常用的思想方法．如图，直线y＝x+5和直线y＝ax+b相交于点P，根据图象可知，方程x+5＝ax+b的解是（　　）

A．x＝20 B．x＝5 C．x＝25 D．x＝15
一十六．平行线的性质（共1小题）
17．（2021•济宁）如图，AB∥CD，BC∥DE，若∠B＝72°28′，那么∠D的度数是（　　）

A．72°28′ B．101°28′ C．107°32′ D．127°32′
一十七．多边形内角与外角（共2小题）
18．（2021•济宁）如图，正五边形ABCDE中，∠CAD的度数为（　　）

A．72° B．45° C．36° D．35°
19．（2020•济宁）一个多边形的内角和是1080°，则这个多边形的边数是（　　）
A．9 B．8 C．7 D．6
一十八．三角形的内切圆与内心（共1小题）
20．（2020•济宁）如图，在△ABC中，点D为△ABC的内心，∠A＝60°，CD＝2，BD＝4．则△DBC的面积是（　　）

A．4 B．2 C．2 D．4
一十九．圆锥的计算（共1小题）
21．（2022•济宁）已知圆锥的母线长8cm，底面圆的直径6cm，则这个圆锥的侧面积是（　　）
A．96πcm2 B．48πcm2 C．33πcm2 D．24πcm2
二十．作图—复杂作图（共1小题）
22．（2021•济宁）如图，已知△ABC．
（1）以点A为圆心，以适当长为半径画弧，交AC于点M，交AB于点N．
（2）分别以M，N为圆心，以大于MN的长为半径画弧，两弧在∠BAC的内部相交于点P．
（3）作射线AP交BC于点D．
（4）分别以A，D为圆心，以大于AD的长为半径画弧，两弧相交于G，H两点．
（5）作直线GH，交AC，AB分别于点E，F．
依据以上作图，若AF＝2，CE＝3，BD＝，则CD的长是（　　）

A． B．1 C． D．4
二十一．翻折变换（折叠问题）（共1小题）
23．（2022•济宁）如图，三角形纸片ABC中，∠BAC＝90°，AB＝2，AC＝3．沿过点A的直线将纸片折叠，使点B落在边BC上的点D处；再折叠纸片，使点C与点D重合，若折痕与AC的交点为E，则AE的长是（　　）

A． B． C． D．
二十二．解直角三角形的应用-方向角问题（共1小题）
24．（2020•济宁）一条船从海岛A出发，以15海里/时的速度向正北航行，2小时后到达海岛B处．灯塔C在海岛A的北偏西42°方向上，在海岛B的北偏西84°方向上．则海岛B到灯塔C的距离是（　　）
A．15海里 B．20海里 C．30海里 D．60海里
二十三．简单几何体的三视图（共1小题）
25．（2021•济宁）一个圆柱体如图所示，下面关于它的左视图的说法其中正确的是（　　）

A．既是轴对称图形，又是中心对称图形
B．既不是轴对称图形，又不是中心对称图形
C．是轴对称图形，但不是中心对称图形
D．是中心对称图形，但不是轴对称图形
二十四．简单组合体的三视图（共1小题）
26．（2022•济宁）如图是由6个完全相同的小正方体搭建而成的几何体，则这个几何体的主视图是（　　）
A． B． C． D．
二十五．由三视图判断几何体（共1小题）
27．（2020•济宁）如图是一个几何体的三视图，根据图中所示数据计算这个几何体的侧面积是（　　）

A．12πcm2 B．15πcm2 C．24πcm2 D．30πcm2
二十六．折线统计图（共1小题）
28．（2022•济宁）某班级开展“共建书香校园”读书活动．统计了1至7月份该班同学每月阅读课外书的本数，并绘制出如图所示的折线统计图．则下列说法正确的是（　　）

A．从2月到6月，阅读课外书的本数逐月下降
B．从1月到7月，每月阅读课外书本数的最大值比最小值多45
C．每月阅读课外书本数的众数是45
D．每月阅读课外书本数的中位数是58
二十七．方差（共1小题）
29．（2020•济宁）下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩（单位：cm）的平均数和方差，要从中选择一名成绩较高且发挥稳定的运动员参加决赛，最合适的运动员是（　　）

甲
乙
丙
丁
平均数
376
350
376
350
方差s2
12.5
13.5
2.4
5.4
A．甲 B．乙 C．丙 D．丁
二十八．概率公式（共1小题）
30．（2020•济宁）小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案（如图所示），每个图案中他只在最下面的正方体上写“心”字，寓意“不忘初心”．其中第（1）个图案中有1个正方体，第（2）个图案中有3个正方体，第（3）个图案中有6个正方体，…按照此规律，从第（100）个图案所需正方体中随机抽取一个正方体，抽到带“心”字正方体的概率是（　　）

A． B． C． D．

山东省济宁市三年（2020-2022）中考数学真题分类汇编-选择题
参考答案与试题解析
一．正数和负数（共1小题）
1．（2021•济宁）若盈余2万元记作+2万元，则﹣2万元表示（　　）
A．盈余2万元 B．亏损2万元
C．亏损﹣2万元 D．不盈余也不亏损
【解答】解：﹣2万元表示亏损2万元，
故选：B．
二．相反数（共1小题）
2．（2020•济宁）﹣的相反数是（　　）
A．﹣ B．﹣ C． D．
【解答】解：﹣的相反数是：．
故选：D．
三．近似数和有效数字（共2小题）
3．（2022•济宁）用四舍五入法取近似值，将数0.0158精确到0.001的结果是（　　）
A．0.015 B．0.016 C．0.01 D．0.02
【解答】解：0.0158≈0.016，
故选：B．
4．（2020•济宁）用四舍五入法将数3.14159精确到千分位的结果是（　　）
A．3.1 B．3.14 C．3.142 D．3.141
【解答】解：3.14159精确到千分位的结果是3.142．
故选：C．
四．规律型：数字的变化类（共1小题）
5．（2021•济宁）按规律排列的一组数据：，，□，，，，…，其中□内应填的数是（　　）
A． B． C． D．
【解答】解：观察这排数据发现：分子为连续的奇数，分母为序号的平方+1，
∴第n个数据为：．
当n＝3时，□的分子为5，分母＝32+1＝10，
∴这个数为＝，
故选：D．
五．规律型：图形的变化类（共1小题）
6．（2022•济宁）如图，用相同的圆点按照一定的规律拼出图形．第一幅图4个圆点，第二幅图7个圆点，第三幅图10个圆点，第四幅图13个圆点……按照此规律，第一百幅图中圆点的个数是（　　）

A．297 B．301 C．303 D．400
【解答】解：观察图形可知：
摆第1个图案需要4个圆点，即4+3×0；
摆第2个图案需要7个圆点，即4+3＝4+3×1；
摆第3个图案需要10个圆点，即4+3+3＝4+3×2；
摆第4个图案需要13个圆点，即4+3+3+3＝4+3×3；
…
第n个图摆放圆点的个数为：4+3（n﹣1）＝3n+1，
∴第100个图放圆点的个数为：3×100+1＝301．
故选：B．
六．同底数幂的除法（共1小题）
7．（2021•济宁）下列各式中，正确的是（　　）
A．x+2x＝3x2 B．﹣（x﹣y）＝﹣x﹣y
C．（x2）3＝x5 D．x5÷x3＝x2
【解答】解：A、应为x+2x＝3x，故本选项错误；
B、应为﹣（x﹣y）＝﹣x+y，故本选项错误；
C、（x2）3＝x2×3＝x6，故本选项错误；
D、x5÷x3＝x5﹣3＝x2，故本选项正确．
故选：D．
七．因式分解的意义（共1小题）
8．（2022•济宁）下面各式从左到右的变形，属于因式分解的是（　　）
A．x2﹣x﹣1＝x（x﹣1）﹣1 B．x2﹣1＝（x﹣1）2
C．x2﹣x﹣6＝（x﹣3）（x+2） D．x（x﹣1）＝x2﹣x
【解答】解：A选项不是因式分解，故不符合题意；
B选项计算错误，故不符合题意；
C选项是因式分解，故符合题意；
D选项不是因式分解，故不符合题意；
故选：C．
八．分式的混合运算（共1小题）
9．（2021•济宁）计算÷（a+1﹣）的结果是（　　）
A． B．
C． D．
【解答】解：原式＝÷[]
＝÷
＝
＝，
故选：A．
九．零指数幂（共1小题）
10．（2022•济宁）下列各式运算正确的是（　　）
A．﹣3（x﹣y）＝﹣3x+y B．x3•x2＝x6
C．（π﹣3.14）0＝1 D．（x3）2＝x5
【解答】解：∵﹣3（x﹣y）＝﹣3x+3y，
∴A选项的结论不正确；
∵x3•x2＝x3+2＝x5，
∴B选项的结论不正确；
∵（π﹣3.14）0＝1，
∴C选项的结论正确；
∵（x3）2＝x6，
∴D选项的结论不正确，
故选：C．
一十．最简二次根式（共1小题）
11．（2020•济宁）下列各式是最简二次根式的是（　　）
A． B． C． D．
【解答】解：A、是最简二次根式，符合题意；
B、＝2，不是最简二次根式，不符合题意；
C、＝a，不是最简二次根式，不符合题意；
D、＝，不是最简二次根式，不符合题意．
故选：A．
一十一．根与系数的关系（共1小题）
12．（2021•济宁）已知m，n是一元二次方程x2+x﹣2021＝0的两个实数根，则代数式m2+2m+n的值等于（　　）
A．2019 B．2020 C．2021 D．2022
【解答】解：∵m，n是一元二次方程x2+x﹣2021＝0的两个实数根，
∴m2+m＝2021，m+n＝﹣1，
∴m2+2m+n＝（m2+m）+（m+n）＝2021+（﹣1）＝2020．
故选：B．
一十二．由实际问题抽象出分式方程（共1小题）
13．（2022•济宁）一辆汽车开往距出发地420km的目的地，若这辆汽车比原计划每小时多行10km，则提前1小时到达目的地．设这辆汽车原计划的速度是xkm/h，根据题意所列方程是（　　）
A．＝+1 B．+1＝
C．＝+1 D．+1＝
【解答】解：∵这辆汽车比原计划每小时多行10km，且这辆汽车原计划的速度是xkm/h，
∴这辆汽车提速后的速度是（x+10）km/h．
依题意得：＝+1，
故选：C．
一十三．解一元一次不等式组（共1小题）
14．（2021•济宁）不等式组的解集在数轴上表示正确的是（　　）
A．
B．
C．
D．
【解答】解：，
解不等式①，得x≥﹣1，
解不等式②，得x＜3，
所以不等式组的解集是﹣1≤x＜3，
在数轴上表示出来为：
，
故选：B．
一十四．一元一次不等式组的整数解（共1小题）
15．（2022•济宁）若关于x的不等式组仅有3个整数解，则a的取值范围是（　　）
A．﹣4≤a＜﹣2 B．﹣3＜a≤﹣2 C．﹣3≤a≤﹣2 D．﹣3≤a＜﹣2
【解答】解：解不等式x﹣a＞0得：x＞a，
解不等式7﹣2x＞5得：x＜1，
∵关于x的不等式组仅有3个整数解，
∴﹣3≤a＜﹣2，
故选：D．
一十五．一次函数与一元一次方程（共1小题）
16．（2020•济宁）数形结合是解决数学问题常用的思想方法．如图，直线y＝x+5和直线y＝ax+b相交于点P，根据图象可知，方程x+5＝ax+b的解是（　　）

A．x＝20 B．x＝5 C．x＝25 D．x＝15
【解答】解：∵直线y＝x+5和直线y＝ax+b相交于点P（20，25）
∴方程x+5＝ax+b的解为x＝20．
故选：A．
一十六．平行线的性质（共1小题）
17．（2021•济宁）如图，AB∥CD，BC∥DE，若∠B＝72°28′，那么∠D的度数是（　　）

A．72°28′ B．101°28′ C．107°32′ D．127°32′
【解答】解：∵AB∥CD，∠B＝72°28′，
∴∠C＝∠B＝72°28′，
∵BC∥DE，
∴∠D+∠C＝180°，
∴∠D＝180°﹣∠C＝107°32′，
故选：C．
一十七．多边形内角与外角（共2小题）
18．（2021•济宁）如图，正五边形ABCDE中，∠CAD的度数为（　　）

A．72° B．45° C．36° D．35°
【解答】解：根据正多边形内角和公式可得，
正五边形ABCDE的内角和＝180°×（5﹣2）＝540°，
则∠BAE＝∠B＝∠E＝＝108°，
根据正五边形的性质，△ABC≌△AED，
∴∠CAB＝∠DAE＝（180°﹣108°）＝36°，
∴∠CAD＝108°﹣36°﹣36°＝36°，
故选：C．
19．（2020•济宁）一个多边形的内角和是1080°，则这个多边形的边数是（　　）
A．9 B．8 C．7 D．6
【解答】解：设所求n边形边数为n，
则1080°＝（n﹣2）•180°，
解得n＝8．
故选：B．
一十八．三角形的内切圆与内心（共1小题）
20．（2020•济宁）如图，在△ABC中，点D为△ABC的内心，∠A＝60°，CD＝2，BD＝4．则△DBC的面积是（　　）

A．4 B．2 C．2 D．4
【解答】解：过点B作BH⊥CD的延长线于点H．
∵点D为△ABC的内心，∠A＝60°，
∴∠DBC+∠DCB＝（∠ABC+∠ACB）＝（180°﹣∠A），
∴∠BDC＝90°+∠A＝90°+×60°＝120°，
则∠BDH＝60°，
∵BD＝4，
∴DH＝2，BH＝2，
∵CD＝2，
∴△DBC的面积＝CD•BH＝＝2，
故选：B．

一十九．圆锥的计算（共1小题）
21．（2022•济宁）已知圆锥的母线长8cm，底面圆的直径6cm，则这个圆锥的侧面积是（　　）
A．96πcm2 B．48πcm2 C．33πcm2 D．24πcm2
【解答】解：∵底面圆的直径为6cm，
∴底面圆的半径为3cm，
∴圆锥的侧面积＝×8×2π×3＝24πcm2．
故选：D．
二十．作图—复杂作图（共1小题）
22．（2021•济宁）如图，已知△ABC．
（1）以点A为圆心，以适当长为半径画弧，交AC于点M，交AB于点N．
（2）分别以M，N为圆心，以大于MN的长为半径画弧，两弧在∠BAC的内部相交于点P．
（3）作射线AP交BC于点D．
（4）分别以A，D为圆心，以大于AD的长为半径画弧，两弧相交于G，H两点．
（5）作直线GH，交AC，AB分别于点E，F．
依据以上作图，若AF＝2，CE＝3，BD＝，则CD的长是（　　）

A． B．1 C． D．4
【解答】解：由作法得AD平分∠BAC，EF垂直平分AD，
∴∠EAD＝∠FAD，EA＝ED，FA＝FD，
∵EA＝ED，
∴∠EAD＝∠EDA，
∴∠FAD＝∠EDA，
∴DE∥AF，
同理可得AE∥DF，
∴四边形AEDF为平行四边形，
而EA＝ED，
∴四边形AEDF为菱形，
∴AE＝AF＝2，
∵DE∥AB，
∴＝，即＝，
∴CD＝．
故选：C．

二十一．翻折变换（折叠问题）（共1小题）
23．（2022•济宁）如图，三角形纸片ABC中，∠BAC＝90°，AB＝2，AC＝3．沿过点A的直线将纸片折叠，使点B落在边BC上的点D处；再折叠纸片，使点C与点D重合，若折痕与AC的交点为E，则AE的长是（　　）

A． B． C． D．
【解答】解：∵沿过点A的直线将纸片折叠，使点B落在边BC上的点D处，
∴AD＝AB＝2，∠B＝∠ADB，
∵折叠纸片，使点C与点D重合，
∴CE＝DE，∠C＝∠CDE，
∵∠BAC＝90°，
∴∠B+∠C＝90°，
∴∠ADB+∠CDE＝90°，
∴∠ADE＝90°，
∴AD2+DE2＝AE2，
设AE＝x，则CE＝DE＝3﹣x，
∴22+（3﹣x）2＝x2，
解得x＝，
∴AE＝，
故选：A．
二十二．解直角三角形的应用-方向角问题（共1小题）
24．（2020•济宁）一条船从海岛A出发，以15海里/时的速度向正北航行，2小时后到达海岛B处．灯塔C在海岛A的北偏西42°方向上，在海岛B的北偏西84°方向上．则海岛B到灯塔C的距离是（　　）
A．15海里 B．20海里 C．30海里 D．60海里
【解答】解：如图．
根据题意得：∠CBD＝84°，∠CAB＝42°，
∴∠C＝∠CBD﹣∠CAB＝42°＝∠CAB，
∴BC＝AB，
∵AB＝15×2＝30（海里），
∴BC＝30（海里），
即海岛B到灯塔C的距离是30海里．
故选：C．

二十三．简单几何体的三视图（共1小题）
25．（2021•济宁）一个圆柱体如图所示，下面关于它的左视图的说法其中正确的是（　　）

A．既是轴对称图形，又是中心对称图形
B．既不是轴对称图形，又不是中心对称图形
C．是轴对称图形，但不是中心对称图形
D．是中心对称图形，但不是轴对称图形
【解答】解：圆柱体的左视图是长方形，而长方形既是轴对称图形，也是中心对称图形，
故选：A．
二十四．简单组合体的三视图（共1小题）
26．（2022•济宁）如图是由6个完全相同的小正方体搭建而成的几何体，则这个几何体的主视图是（　　）
A． B． C． D．
【解答】解：几何体的主视图如下：

故选：A．

二十五．由三视图判断几何体（共1小题）
27．（2020•济宁）如图是一个几何体的三视图，根据图中所示数据计算这个几何体的侧面积是（　　）

A．12πcm2 B．15πcm2 C．24πcm2 D．30πcm2
【解答】解：由三视图可知，原几何体为圆锥，
∵l＝＝5（cm），
∴S侧＝•2πr•l＝×2π××5＝15π（cm2）．
故选：B．
二十六．折线统计图（共1小题）
28．（2022•济宁）某班级开展“共建书香校园”读书活动．统计了1至7月份该班同学每月阅读课外书的本数，并绘制出如图所示的折线统计图．则下列说法正确的是（　　）

A．从2月到6月，阅读课外书的本数逐月下降
B．从1月到7月，每月阅读课外书本数的最大值比最小值多45
C．每月阅读课外书本数的众数是45
D．每月阅读课外书本数的中位数是58
【解答】解：∵5月份阅读课外书的本数有所上升，
故A选项不符合题意；
∵从1月到7月，每月阅读课外书本数的最大值比最小值多50，
故B选项不符合题意；
∵每月阅读课外书本数的众数是58，
故C选项不符合题意；
∵每月阅读课外书本数的中位数是58，
故D选项符合题意；
故选：D．
二十七．方差（共1小题）
29．（2020•济宁）下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩（单位：cm）的平均数和方差，要从中选择一名成绩较高且发挥稳定的运动员参加决赛，最合适的运动员是（　　）

甲
乙
丙
丁
平均数
376
350
376
350
方差s2
12.5
13.5
2.4
5.4
A．甲 B．乙 C．丙 D．丁
【解答】解：∵乙和丁的平均数最小，
∴从甲和丙中选择一人参加比赛，
∵丙的方差最小，
∴选择丙参赛．
故选：C．
二十八．概率公式（共1小题）
30．（2020•济宁）小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案（如图所示），每个图案中他只在最下面的正方体上写“心”字，寓意“不忘初心”．其中第（1）个图案中有1个正方体，第（2）个图案中有3个正方体，第（3）个图案中有6个正方体，…按照此规律，从第（100）个图案所需正方体中随机抽取一个正方体，抽到带“心”字正方体的概率是（　　）

A． B． C． D．
【解答】解：∵第1个图形中正方体的个数为1，
第2个图形中正方体的个数3＝1+2，
第3个图形中正方体的个数6＝1+2+3，
∴第100个图形中，正方体一共有1+2+3+……+99+100＝＝5050（个），其中写有“心”字的正方体有100个，
∴抽到带“心”字正方体的概率是＝，
故选：D．