

2023天一大联考顶尖计划高三上学期第一次联考理科数学试题含答案
展开“顶尖计划”2023届高中毕业班第一次考试
理科数学
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合,则中的元素个数为
A. 8 B. 9 C. 10 D. 11
2. 已知复数, 则
A. 1 B. C. D. 3
3. 已知非零向量满足,且,则
A. B. C. D.
4. 某士兵进行射击训练,每次命中目标的概率均为,且每次命中与否相互独立,则他连续射击3次,至少命中两次的概率为
A. B. C. D.
5. 已知函数在处取得最大值,则
A. B. C. D.
6. 已知定义域为的偶函数满足,且当时,,则
A. B. C. 1 D. 3
7. 我国古代经典数学名著《九章算术》中有一段表述:“今有圆堡壔( dăo ),周四丈八尺,高一丈一尺”,意思是有一个圆柱,底面周长为4丈8尺,高为1丈1尺.则该圆柱的外接球的表面积约为 (注:1丈=10尺,取3)
A. 1185 平方尺 B. 1131 平方尺 C. 674 平方尺 D. 337 平方尺
8. 甲、乙、丙、丁、戊五名志愿者去三个不同的小区参加新冠疫情防控志愿服务, 每个小区至少去1人,每人只去1个小区,且甲、乙去同一个小区, 则不同的安排方法有
A. 28 种 B. 32 种 C. 36 种 D. 42 种
9. 已知角的顶点在坐标原点,始边与轴的非负半轴重合,终边经过点,其中, 若 ,则
A. 2 B. C. D.
10. 过抛物线的焦点且斜率为-1的直线交于(其中A在轴上方)两点,交的准线于点,且,为坐标原点,则
A. 2 B. C. D.
11. 已知是奇函数,则过点向曲线可作的切线条数是
A. 1 B. 2 C. 3 D. 不确定
12、设双曲线的左、右焦点分别为点,过点且斜率为的直线与双曲线的左、右两支分别交于两点,若 ,且直线的斜率为 3,则的离心率为
A. B. C. D.
二、填空题: 本题共4小题,每小题5分,共 20 分.
13. 已知函数在区间上有且仅有一个零点,则实数的取值范围为_____.
14. 写出一个同时具有下列性质①②③的函数:_____.
① ;②当时,单调递减; ③为偶函数.
15. 已知平面上的动点到点和的距离之比为,则点到轴的距离最大值为_____.
16. 微型航空遥感技术以无人机为空中遥感平台,为城市经济和文化建设提供了有效的技术服务手段.如图所示, 有一架无人机在空中处进行航拍,水平地面上甲、乙两人分别在处观察该无人机(两人的身高忽略不计),为无人机在水平地面上的正投影.已知甲乙两人相距100 m,甲观察无人机的仰角为,若再测量两个角的大小就可以确定无人机的飞行高度,则这两个角可以是_____ .(写出所有符合要求的编号)
①和;②和;
③和;④和.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
(一) 必考题:共 60 分.
17. (12 分)
设等差数列的前项和为,已知.
(I) 求数列的通项公式;
(II) 若,求数列的前项和.
18. (12 分)
某工厂共有甲、乙两个车间,为了比较两个车间的生产水平,分别从两个车间生产的同一种零件中各随机抽取了100件, 它们的质量指标值统计如下:
质量指标值 | |||||
甲车间(件) | 15 | 20 | 25 | 31 | 9 |
乙车间(件) | 5 | 10 | 15 | 39 | 31 |
(I)估计该工厂生产这种零件的质量指标值的平均数;(同一组中的数据用该组区间的中点值作代表)
(II)根据所给数据,完成下面的列联表(表中数据单位:件),并判断是否有的把握认为甲、乙两个车间的生产水平有差异.
| ||
甲车间 |
|
|
乙车间 |
|
|
附:,其中.
0.05 | 0.01 | 0.001 | |
k | 3.841 | 6.635 | 10.828 |
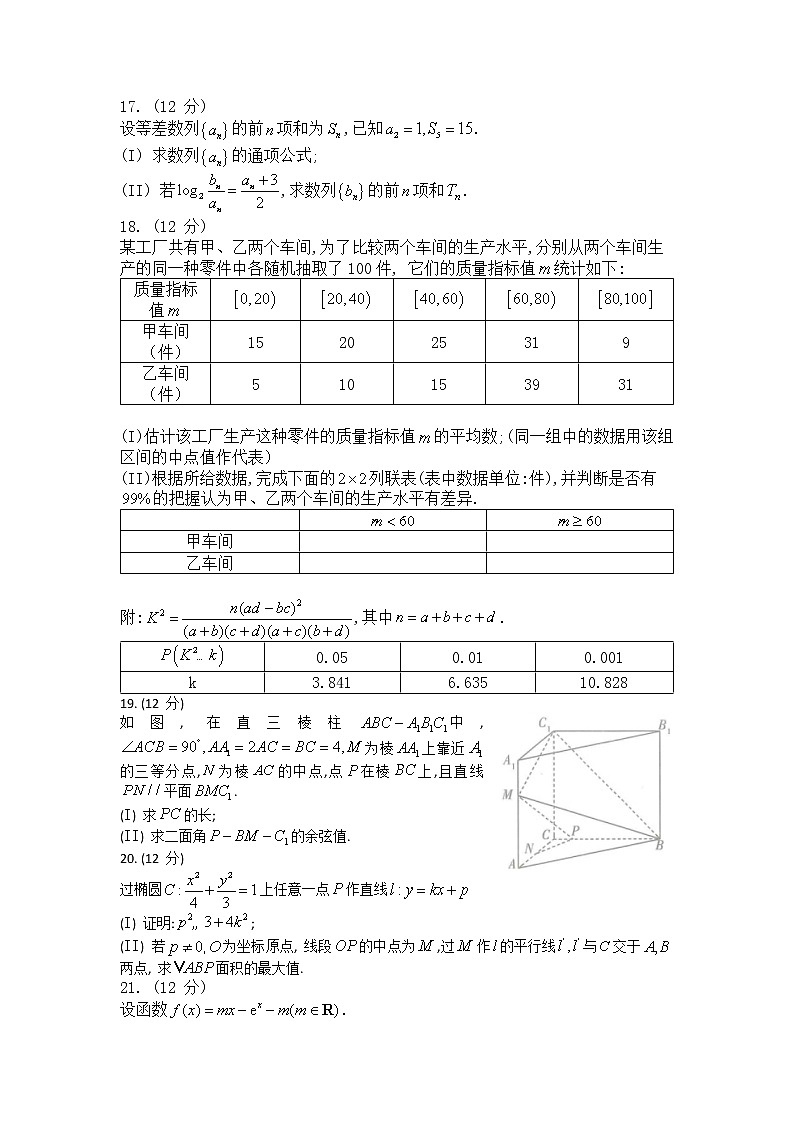
19. (12 分)
如图, 在直三棱柱中,为棱上靠近的三等分点,为棱的中点,点在棱上,且直线平面.
(I) 求的长;
(II) 求二面角的余弦值.
20. (12 分)
过椭圆上任意一点作直线
(I) 证明:;
(II) 若为坐标原点, 线段的中点为,过作的平行线与交于两点, 求面积的最大值.
21. (12 分)
设函数.
(I) 讨论的单调性;
(II) 若有两个零点和,设,证明:(为的导函数).
(二)选考题:共10分.请考生在22,23题中任选一题作答,如果多做,则按所做的第一题计分.
22. [选修 4-4:坐标系与参数方程] (10 分)
在直角坐标系中,曲线的参数方程为以为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为.
(I) 写出的直角坐标方程;
(II) 若与只有一个公共点,求的值.
23. [选修 4-5:不等式选讲] (10 分)
已知均为正实数, 且.
(I) 求的最小值;
(II) 证明: .
理科数学参考答案
一、选择题
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | B | C | C | A | A | D | B | C | D | D | C | B |
二、填空题
13. 14.(不唯一) 15. 16.①③④
三、解答题:
17.解析(I)设数列的公差为,由题设可得 解得
所以.
(II)由条件可得 ,
①
②
②减①可得:
18.解析 (I)由所给数据,各组的频率分别为 0.1,0.15,0.2,0.35,0.2
所以该工厂生产这种零件的质量指标值的平均数的估计值为
(Ⅱ)列联表如下:
| ||
甲车间 | 60 | 40 |
乙车间 | 30 | 70 |
所以
因为18.182大于6.635,所以有99%把握认为甲乙两个车间的生产水平有差异.
19.解析 ( I )在上取一点, 使得, 连接.
由已知得 , 所以.
因为平面, 所以平面.
又因为平面
所以平面平面.
根据面面平行的性质可知.
在矩形中, 可得,
所以, 所以.
(II) 以为坐标原点, 分别以所在直线为 轴建立空间直角坐标系.
则.
,
设平面的法向量为 ,,
则,所以,取得
设平面的法向量为,
则
所以取, 得
所以
结合图可知二面角的余弦值为.
20. 解析(I)联立
消去整理得,
因为点在上, 所以
化简得.
(II) 设,点,则.
由已知得, 所以,
即点满足方程,所以.
由 得 ,
设,则.
所以
所以
令,因为, 所以.
所以
所以面积的最大值为.
21. 解析 (I) ,
若, 则,函数在上单调递减
若,令,得
当时,,当时,.
所以在上单调递增, 在上单调递减.
(II) 不妨令, 由题设可得
两式相减整理可得.
所以
令 , 则 ,
要证, 即证 , 即证.
令, 则,
所以在上单调递减
又, 所以,
即成立,所以.
22. 解析 (I) 由的极坐标方程可得, 故其直角坐标方程为.
(II) 由的参数方程可得,
即的普通方程为.
联立方程 得, 因为与只有一个公共点,
所以,
解得.
23. 解析 (I) 由基本不等式可知,当且仅当 , 即 时等号成立,所以的最小值为 6 .
(II) 因为, 所以.
.
同理可得
所以,当且仅当时等号成立
所以,
即
天一大联考顶尖计划2024届高中毕业班第一次考试数学: 这是一份天一大联考顶尖计划2024届高中毕业班第一次考试数学,文件包含数学高三命题报告pdf、数学pdf、数学高三简易答案pdf等3份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
2023届天一大联考(山西省)三晋名校联盟高三下学期顶尖计划联考数学试题含解析: 这是一份2023届天一大联考(山西省)三晋名校联盟高三下学期顶尖计划联考数学试题含解析,共19页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2023天一大联考顶尖计划高三上学期第一次联考文科数学试题含答案: 这是一份2023天一大联考顶尖计划高三上学期第一次联考文科数学试题含答案,共8页。试卷主要包含了 已知集合,则中的元素个数为, 已知复数, 则, 已知非零向量满足,且,则, 设数列满足且,则, 已知函数在处取得最大值,则等内容,欢迎下载使用。












